5.6. Потенциальные векторные поля. Нахождение потенциала

Векторное поле называется потенциальным, если работа в этом поле не зависит от пути интегрирования:

,

что является условием потенциальности поля. Из равенства нулю циркуляции вектора вдоль каждого замкнутого контура следует по формуле Стокса, что =0.

Существует некоторая функция U(x,y,z), для которой выражение Pdx + Qdy + Rdz является полным дифференциалом:

dU = Pdx + Qdy + Rdz. Функция U(М) называется потенциалом векторного поля:

.

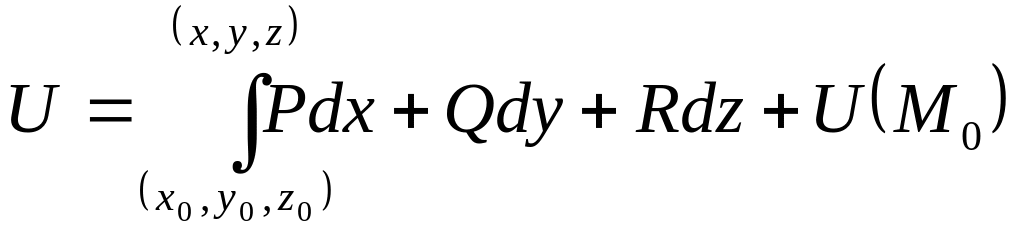Для нахождения потенциала поля по этой формуле лучше всего интегрировать по ломаной линии, соединяющей точки и , звенья которой параллельны осям координат.

Работа потенциального векторного поля вдоль любого пути равна разности значений потенциала этого поля в конце и начале пути: .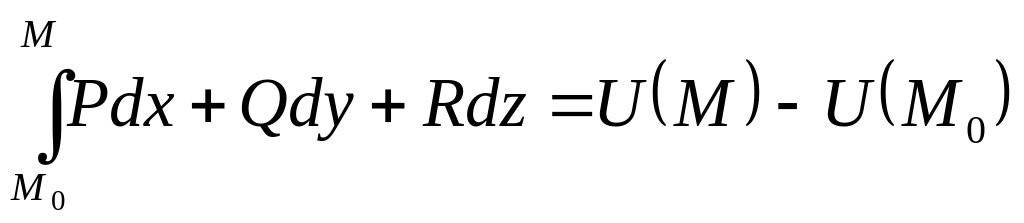

Пример 35. Показать, что поле является потенциальным и найти его потенциал.

Решение:

= =

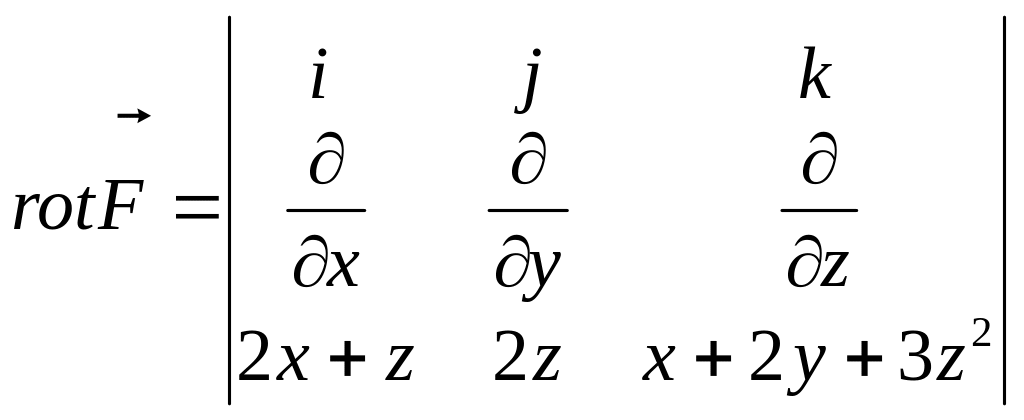= . Ротор равен нулю, следовательно, поле потенциально. Возьмём :

+

+ =

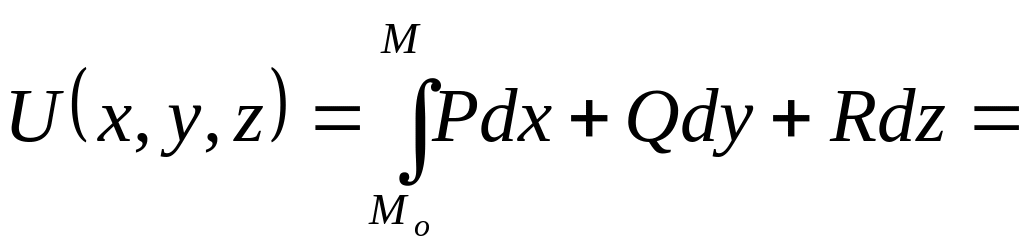
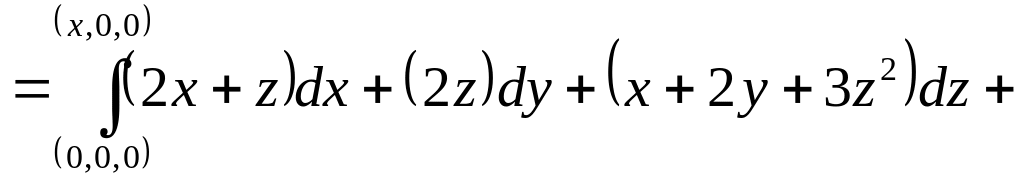
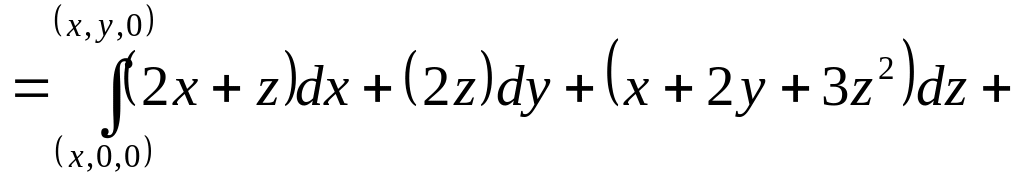
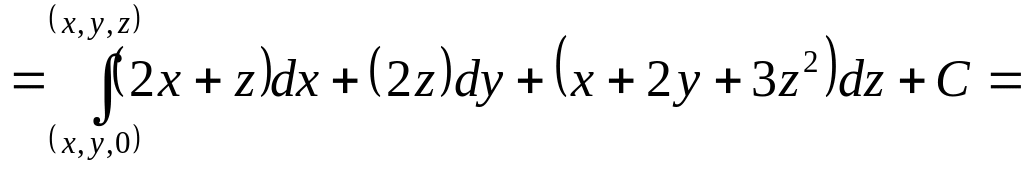
5.7. Оператор Гамильтона. Векторные операции второго порядка

Пусть даны два поля: скалярное поле и векторное поле .

Для скалярного поля можно построить векторное – поле градиента:

,

а по векторному полю можно построить скалярное поле– поле дивергенции: = ,

а так же векторное поле – поле ротора:

.

Операции нахождения градиента, дивергенции и ротора называется дифференциальными операциями первого порядка.

Для того чтобы сделать запись менее громоздкой, используют символический вектор набла , оператор Гамильтона. При этом полагают, что действия оператора набла подчиняются правилам действиями с обычными векторами при условии сохранения порядка сомножителей. Градиент скалярной функции получается как результат действия оператора Гамильтона на скалярную функцию :

.

Дивергенция векторного поля получается в результате скалярного произведения векторов и :

.

Ротор векторного поля получается в результате векторного произведения векторов и :

.

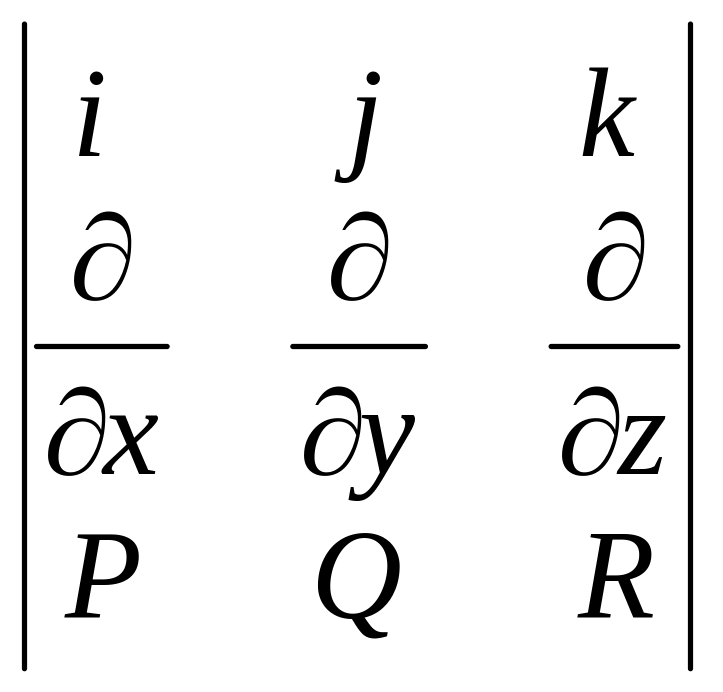Действие оператора на , , даст дифференциальные операции второго порядка над функциями , . Всего таких операций пять. Рассмотрим некоторые из них.

Операция дает оператор Лапласа:

=

. Таким образом, оператор Лапласа равен .

Операция дает тождественный ноль, т.к. операция представляется как векторно-скалярное произведение:

= ,

а векторы и коллинеарные. Векторное поле называется соленоидальным, если дивергенция его равна нулю. Можно сказать, что поле ротора соленоидально.

Операция тоже дает тождественный ноль:

= ,

так как две строки определителя пропорциональны. Поле называется потенциальным или безвихревым, если ротор поля равен нулю. Следовательно, поле градиента – безвихревое, т.е. потенциальное.

Операция может быть представлена следующим образом:

.

Операция может представляться следующим образом: = .

Вопросы для самопроверки

1. Как определяются двухсторонние поверхности?

2. Как определяются односторонние поверхности?

3. Приведите пример односторонней поверхности.

4. Перечислите свойства поверхностного интеграла второго рода.

5. Каким образом поверхностный интеграл второго рода выражается через двойные интегралы?

6. Как находится знак перед двойным интегралом при

расписывании поверхностного интеграла второго рода в виде суммы двойных интегралов?

7. Сформулируйте теорему Остроградского.

8. Что такое дивергенция векторного поля?

9. Дайте определение поля.

10. Перечислите свойства дивергенции.

11. Выведите формулу Стокса.

12. Что такое ротор векторного поля?

13. Перечислите свойства ротора векторного поля.

14. Когда векторное поле имеет потенциал?

15. Каким образом дивергенция, ротор, и градиент представляются с помощью оператора Гамильтона?

16. Что такое векторные операции второго порядка?

17. Почему и тожественно равны нулю?

18. Какое векторное поле называется соленоидальным?