
- •Введение
- •1. Распределенные атаки на информационно-телекоммуникационные системы
- •1.1. Информационно-телекоммуникационные системы в контексте обеспечения их безопасности
- •1.1.1. Понятийный аппарат в сфере обеспечения безопасности
- •1.1.2. Свойства информационно-телекоммуникационных систем
- •1.1.3. Особенности построения информационно-телекоммуникационных систем
- •1.2. Распределенные атаки типа «отказ в обслуживании» как угроза безопасности в информационно-телекоммуникационных системах
- •1.2.1. Классификация механизмов реализации dDoS-атак
- •1.2.2. Типы dDoS-атак
- •1.2.3 Противодействие dDoS-атакам
- •2. Ddos-атаки на мультисерверные информационно-телекоммуникационные системы
- •2.1. Особенности мультисерверных систем
- •Vip для реальных серверов
- •2.2. DDoS-атаки на мультисерверную систему
- •2.3. Антропогенные источники угроз реализации dDoS-атак на мультисерверные системы
- •2.4. DDoS-атаки как источник информационных рисков в мультисерверной системе
- •2.5. Модели управления рисками мультисерверных систем
- •Обоснование закона распределения ущерба при реализации dDoS-атак на мультисерверную систему
- •3. Аналитическая оценка рисков атакуемых мультисерверных систем
- •3.1. Оценка параметров риска для компонентов мультисерверных систем
- •3.2. Оценка и регулирование рисков мультисерверных систем
- •3.3. Выбор параметров функций рисков компонентов мультисерверной системы
- •4. Управление рисками атакуемых мультисерверных систем
- •4.1. Управление рисками мультисерверных систем в случае ddos-атак на их компоненты
- •4.2. Управление общим риском системы
- •4.3. Подход к параметрическому синтезу системы с заданным риском
- •4.4. Пример практических расчетов
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
4.3. Подход к параметрическому синтезу системы с заданным риском
Пусть
теперь задан требуемый вид общей функции
риска, а, следовательно, и максимально
допустимый диапазон ущербов, причем
график этой функции колеблется в заданной
полосе неравномерности
.
В данном случае важны значения аргумента
![]() ,
при которых общая функция риска достигает
своих экстремумов, и ее значения в данных
точках
,
при которых общая функция риска достигает
своих экстремумов, и ее значения в данных
точках
![]() .
Получим аналитические выражения для
параметров функций рисков компонентов
таким образом, чтобы найденный общий
риск системы соответствовал заданному
виду.
.
Получим аналитические выражения для
параметров функций рисков компонентов
таким образом, чтобы найденный общий
риск системы соответствовал заданному
виду.
В силу гладкости
функции плотности распределения
вероятностей, при предельно допустимых
значениях коэффициента загрузки
центрального процессора
![]() ,
поведение функции риска всей системы,
время отказов компонентов которой
задается функцией плотности распределения
вероятностей Вейбулла, будет зависеть
от ее поведения около точек локальных
экстремумов.
,
поведение функции риска всей системы,
время отказов компонентов которой
задается функцией плотности распределения
вероятностей Вейбулла, будет зависеть
от ее поведения около точек локальных
экстремумов.
Задавая ее значения
в точках
![]() и
и
![]() ,
составим систему уравнений, приравнивая
общую функцию синтезируемой системы,
вычисленную в точках экстремумов, к
значениям заданной общей функции риска
в тех же точках.
,
составим систему уравнений, приравнивая
общую функцию синтезируемой системы,
вычисленную в точках экстремумов, к
значениям заданной общей функции риска
в тех же точках.
В результате
получим систему для нахождения предельно
допустимых значений коэффициента
загрузки центрального процессора
следующей итерации через их значения
в предыдущей вариации. Начальные значения
предварительно задаются. Таким образом,
получаем нелинейную систему относительно
параметров
и
![]() компонентов синтезируемой системы:
компонентов синтезируемой системы:
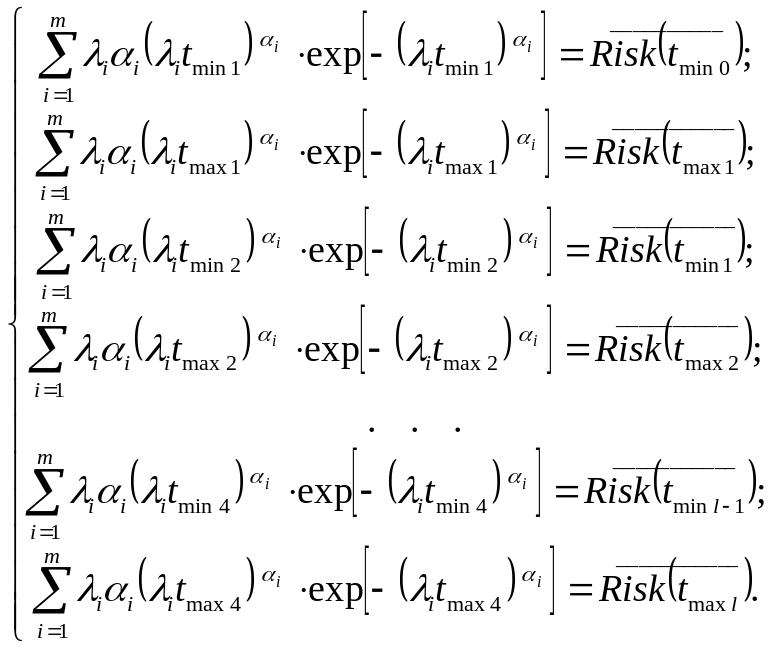 (4.10)
(4.10)
Из системы (4.10) получаем следующую систему для нахождения предельно допустимых значений коэффициента загрузки центрального процессора и максимального числа открытых соединений для каждого сервера синтезируемой МСС:
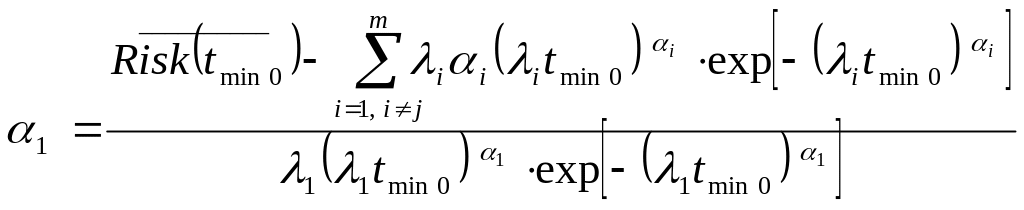 ;
;
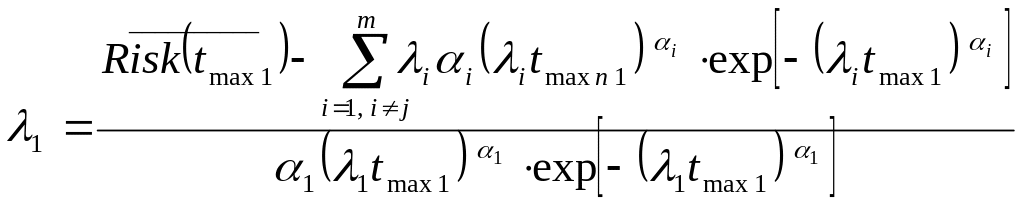 ;
;
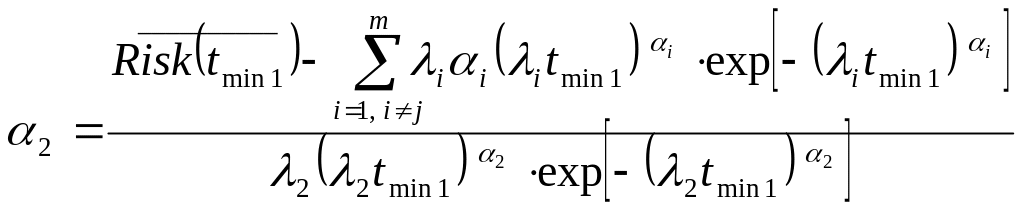 ;
;
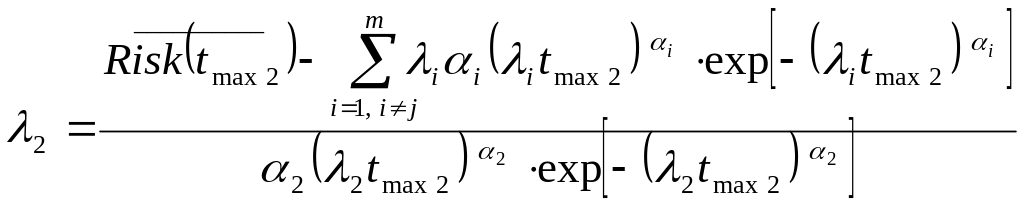 ;
;
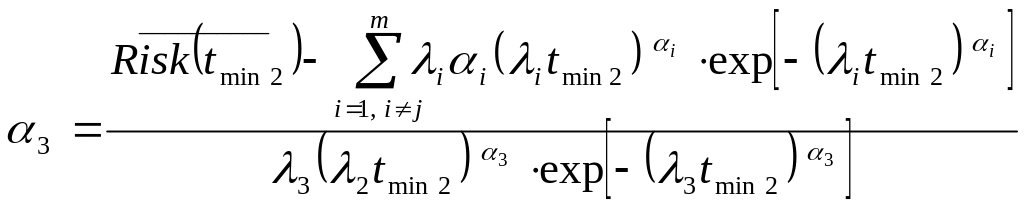 .
.
И так далее. Если
задано
-е
приближение
![]() ,
,
![]() ,
то
,
то
![]() -е
приближение находим по формулам [71]:
-е
приближение находим по формулам [71]:
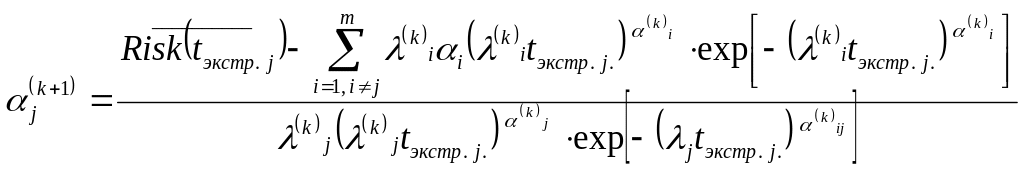 ;
;
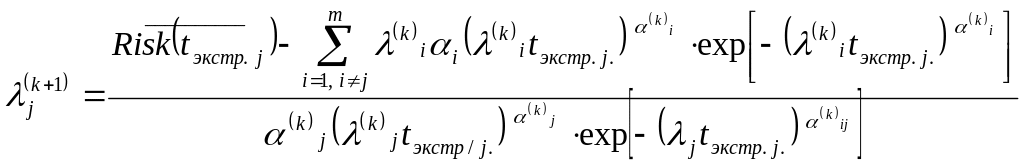 ,
,
где
![]() .
.
Начальные значения
предварительно задаются. Так как функция
риска, заданная с помощью распределения
Вейбулла, имеет максимальное значение
при значении аргумента
![]() ,
то за начальные значения параметров
можно взять
,
то за начальные значения параметров
можно взять
![]() .
Тогда соответствующие параметры
можно выбрать из условия равенства
пиковых значений.
.
Тогда соответствующие параметры
можно выбрать из условия равенства
пиковых значений.
За начальные
значения можно принять значения
параметров компонентов мультисерверной
системы, найденные ранее при условии
уравнивания максимальных значений
функций рисков компонент [70,73]. Если
задано
-е
приближение
![]() ,
,
то
-е
приближение находим по формулам [71].
,
,
то
-е
приближение находим по формулам [71].
В силу гладкости функции плотности распределения вероятности Вейбулла, метод итераций сходится к искомому решению. Для того чтобы получить решение с заданной точностью, необходимо продолжать процесс до тех пор, пока два последовательных приближения будет совпадать с этой точностью. Таким образом, получены параметры компонентов функций риска синтезируемой мультисерверной системы по заданным параметрам общей функции риска и диапазона предельно допустимого ущерба.
В случае, например,
четырех компонент функция риска будет
содержать восемь параметров:
и
,
![]() ,
а локальных экстремумов будет семь:
четыре максимума и три минимума. Поэтому
для нахождения параметров функций
рисков компонентов системы, обеспечивающих
колебание общей функции риска в заданной
полосе неравномерности, будем составлять
две системы нелинейных уравнений
относительно искомых параметров. Первую
систему составим относительно искомых
параметров
,
а локальных экстремумов будет семь:
четыре максимума и три минимума. Поэтому
для нахождения параметров функций
рисков компонентов системы, обеспечивающих
колебание общей функции риска в заданной
полосе неравномерности, будем составлять
две системы нелинейных уравнений
относительно искомых параметров. Первую
систему составим относительно искомых
параметров
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() параметров функций рисков компонент
системы соответственно
,
,
,
,
,
параметров функций рисков компонент
системы соответственно
,
,
,
,
,
![]() ,
,
![]() .
Тогда в качестве вариаций, обеспечивающих
заданное движение риска, будем выбирать
следующие значения:
.
Тогда в качестве вариаций, обеспечивающих
заданное движение риска, будем выбирать
следующие значения:
![]() ,
,
![]() ,
,
![]() ,
,
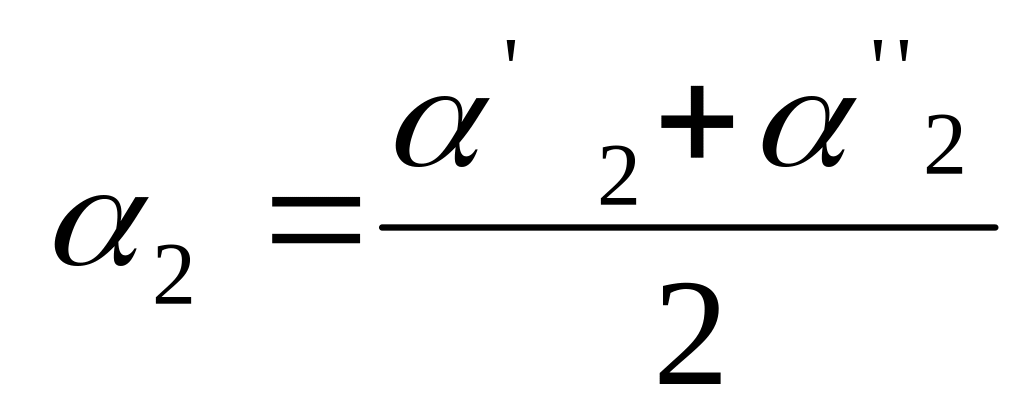 ,
,
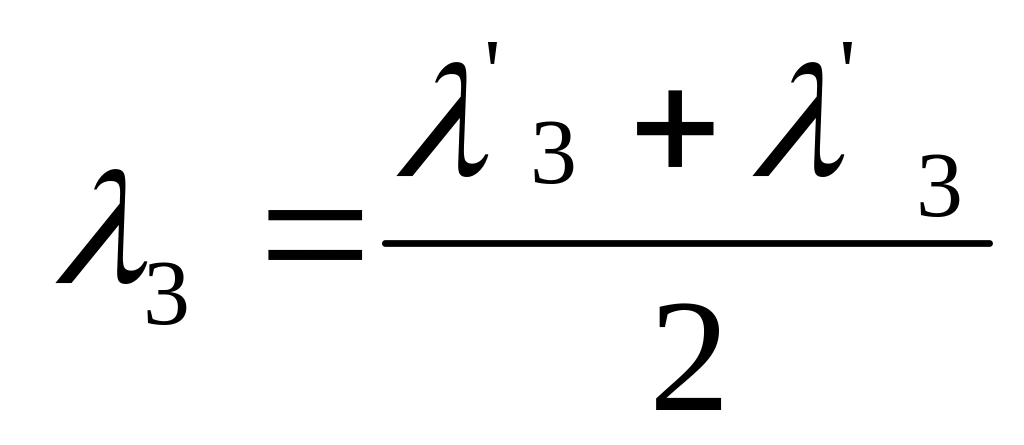 ,
,
![]() ,
,
![]() ,
,
![]() .
.
В рассмотренном примере были заданы следующие значения:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Графики функции общего риска системы при полученных значениях параметров , , , , , , , функций рисков компонент системы в результате 4, 5 и 6 итераций приведены на рис. 4.7.
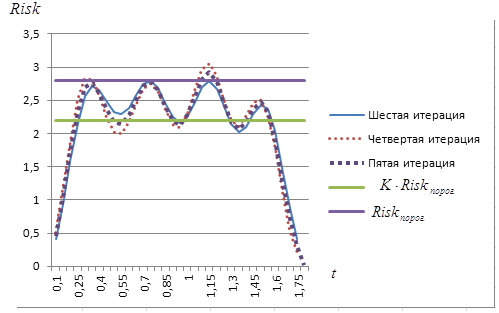
Рис. 4.7. График общей функции риска системы при полученных
значениях параметров функций рисков компонент
После проведения
шестой итерации получаем следующие
значения параметров функций компонент
системы:
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, получены параметры компонентов функций риска синтезируемой МСС по заданному виду общей функции риска и диапазона предельно допустимого ущерба.
Синтез МСС на основе трехпараметрического распределения Вейбулла.
По заданному пороговому значению риска всей системы и полосы неравномерности
![]() (
)
(
)
были получены аналитические выражения для параметров компонентов системы при условии уравнивания максимальных значений функций рисков компонентов [5].
Пусть теперь задан требуемый вид функции риска всей системы, а, следовательно, и максимально допустимый диапазон ущербов, причем график этой функции колеблется в заданной полосе неравномерности . Получим аналитические выражения для параметров функций рисков компонентов таким образом, чтобы найденный общий риск системы соответствовал требуемому виду.
Будем искать заданную общую функцию риска в виде совокупности рисков, имеющих трехпараметрическое распределение Вейбулла:
![]() ,
,
![]() .
.
Тогда риск будет равен
![]() (4.11)
(4.11)
.
Выберем
параметры
![]() таким образом, чтобы максимальное
значение первой волны общей функции
риска
таким образом, чтобы максимальное
значение первой волны общей функции
риска
![]() (4.12)
(4.12)
было рано
.
Так как в этом случае функция риска
компонента достигает своего максимального
значения при
![]() [5], то получаем выражение:
[5], то получаем выражение:
![]() .
.
Отсюда следует соотношение для выбора параметров :
![]() .
(4.13)
.
(4.13)
Затем
полученную функцию риска
![]() сдвигаем вверх по оси риска на величину
сдвигаем вверх по оси риска на величину
![]() .
Тогда максимальное значение первой
волны заданной функции риска будет
равно
.,
а минимальное – не будет меньше
.
.
Тогда максимальное значение первой
волны заданной функции риска будет
равно
.,
а минимальное – не будет меньше
.
Полученный результат иллюстрирует рисунок 4.8.
Вторую волну
заданной функции риска получим, подставив
в выражение (4.11) значение
![]() :
:
![]() .
.
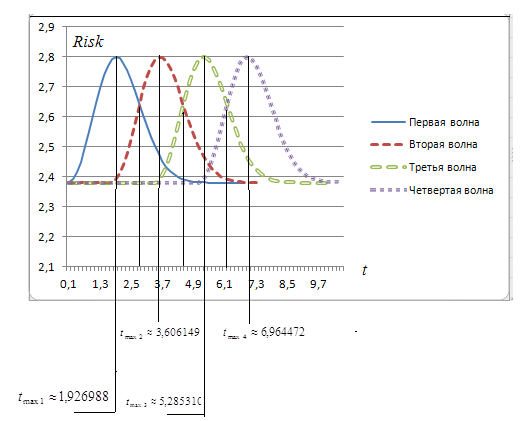
Рис. 4.8. Вид заданной общей функции риска системы
Параметр
![]() будем находить таким образом, чтобы
функция второй волны заданного риска
пересекала функцию первой волны в точке
ее перегиба. Поэтому сначала найдем
точки перегиба функции риска (4.11),
вычислив производную второго порядка
по переменной
будем находить таким образом, чтобы
функция второй волны заданного риска
пересекала функцию первой волны в точке
ее перегиба. Поэтому сначала найдем
точки перегиба функции риска (4.11),
вычислив производную второго порядка
по переменной
![]() ,
и приравняв ее к нулю. Затем определим,
меняет ли производная второго порядка
знак при прохождении через критические
точки.
,
и приравняв ее к нулю. Затем определим,
меняет ли производная второго порядка
знак при прохождении через критические
точки.
Предварительно найдем производную первого порядка:
![]()
![]()
![]() .
.
Далее найдем производную второго порядка по переменной :
![]()
![]()
![]()
![]() .
.
После преобразований получаем следующее уравнение для нахождения критических точек:
![]() .
.
Откуда следует,
что критические точки находим из
квадратного относительно
![]() уравнения:
уравнения:
![]() .
(4.14)
.
(4.14)
Введем
следующее обозначение:
![]() .
.
Тогда уравнение (4.14) будет иметь следующий вид:
![]() .
(4.15)
.
(4.15)
Найдем дискриминант уравнения (4.15):
![]()
![]()
![]() .
.
Определим
знак дискриминанта, рассмотрев квадратное
относительно
![]() уравнение
уравнение
![]() .
(4.16)
.
(4.16)
Так
как знак дискриминанта уравнения (4.16)
![]() ,
коэффициент при
,
коэффициент при
![]() больше нуля, то дискриминант
уравнения (4.15) неотрицателен при всех
значениях
больше нуля, то дискриминант
уравнения (4.15) неотрицателен при всех
значениях
![]() .
Следовательно, при всех значениях
параметра
уравнение (4.14) , значит и уравнение
(4.15), имеют два вещественных корня:
.
Следовательно, при всех значениях
параметра
уравнение (4.14) , значит и уравнение
(4.15), имеют два вещественных корня:
![]() ;
;
![]() .
.
Так как при
прохождении через критические точки
![]() и
и
![]() меняется на противоположный, то они
являются точками перегиба функции
.
Возвращаясь к старой переменной
,
получим следующие выражения для точек
перегиба:
меняется на противоположный, то они
являются точками перегиба функции
.
Возвращаясь к старой переменной
,
получим следующие выражения для точек
перегиба:
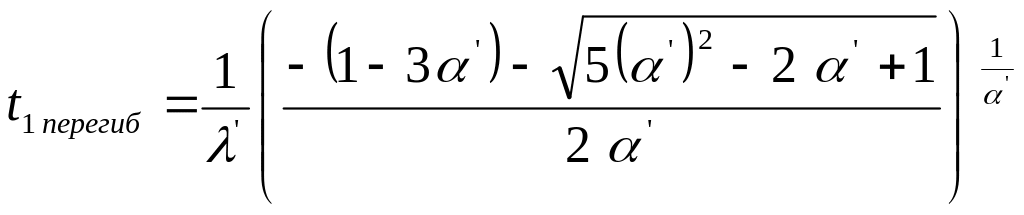 ;
(4.17)
;
(4.17)
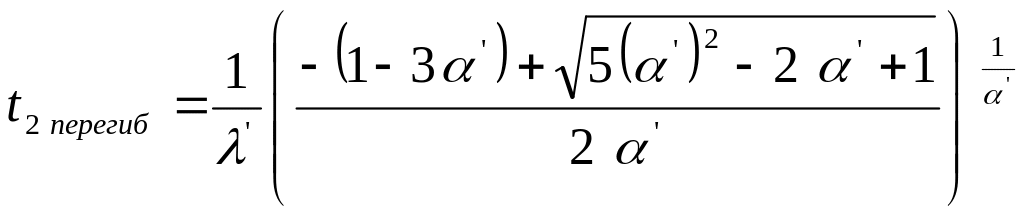 .
(4.18)
.
(4.18)
Параметр
будем находить из уравнения
![]() ,
которое примет следующий вид:
,
которое примет следующий вид:
![]()
![]() .
(4.19)
.
(4.19)
Преобразовав уравнение (4.19), получим следующее уравнение относительно параметра :
![]()
![]() .
.
Откуда получаем:
![]()
![]() .
(4.20)
.
(4.20)
Прологарифмировав обе части уравнения (4.20), получим:
![]()
![]() .
.
Введем следующее
обозначение:
![]() ,
тогда последнее уравнение после
преобразований примет вид:
,
тогда последнее уравнение после
преобразований примет вид:
![]() .
(4.21)
.
(4.21)
Решая
уравнение (4.21) одним из численных методов,
например, методом Ньютона, получим
значение для введенной переменной
![]() .
Тогда, возвращаясь к переменной
,
получим ее значение следующим образом:
.
Тогда, возвращаясь к переменной
,
получим ее значение следующим образом:
![]() .
(4.22)
.
(4.22)
Тогда значение переменной , при котором вторая волна общей функции риска достигает своего максимального значения, т.е. максимальное значение функции, можно найти из соотношения:
![]() ,
(4.23)
,
(4.23)
где .
Получая конкретный
вид требуемой общей функции риска,
колеблющегося в заданной полосе
неравномерности, примем
![]() ,
тогда, исходя из условия (4.13) и учитывая
заданные значение
,
тогда, исходя из условия (4.13) и учитывая
заданные значение
![]() и коэффициента
,
найдем значение параметра
и коэффициента
,
найдем значение параметра
![]() (рис. 4.9). Графическое решение уравнения
(4.21) показано на рис. 4.10.
(рис. 4.9). Графическое решение уравнения
(4.21) показано на рис. 4.10.

Рис. 4.9. Полученные
значения параметров
![]() и
и
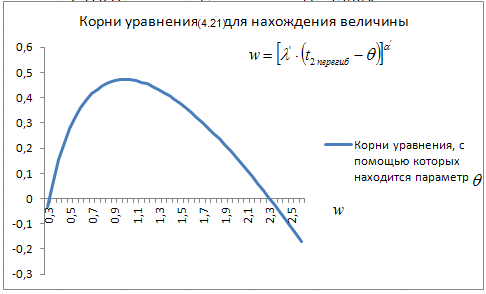
Рис. 4.10. Иллюстрация решения уравнения (4.21)
Получив два корня
уравнения (4.21)
![]() и
и
![]() ,
определяем, что, согласно формуле (4.22),
,
определяем, что, согласно формуле (4.22),
![]() ,
,
![]() ,
следовательно, не подходит. Зная значение
параметра
,
следовательно, не подходит. Зная значение
параметра
![]() ,
по формуле (4.23) находим
,
по формуле (4.23) находим
![]() ,
которые, одновременно, являются и точками
минимума заданной общей функции риска
системы. Значения точек перегиба
,
которые, одновременно, являются и точками
минимума заданной общей функции риска
системы. Значения точек перегиба
![]() ,
полученные по расчетным формулам (4.17),
(4.18), показаны на рис. 4.11.
,
полученные по расчетным формулам (4.17),
(4.18), показаны на рис. 4.11.

Рис. 4.11. Полученные значения переменной , при которых заданная общая функция риска имеет перегибы
Для нахождения параметров компонентов синтезируемой системы воспользуемся на начальном этапе методом итераций для решения нелинейных систем [6]. Для составления уравнений этой системы будем задавать значение общего риска системы в токах экстремумов заданной функции общего риска, которая имеет следующий вид (рисунок 4.10):
 .
.
В силу гладкости
функций плотности распределения Вейбулла
будем получать заданный вид функции
риска. Задавая ее значения в точках
и
![]() ,
составим систему уравнений, приравнивая
общую функцию синтезируемой системы,
вычисленную в точках экстремумов, к
значениям заданной общей функции риска
в тех же точках.
,
составим систему уравнений, приравнивая
общую функцию синтезируемой системы,
вычисленную в точках экстремумов, к
значениям заданной общей функции риска
в тех же точках.
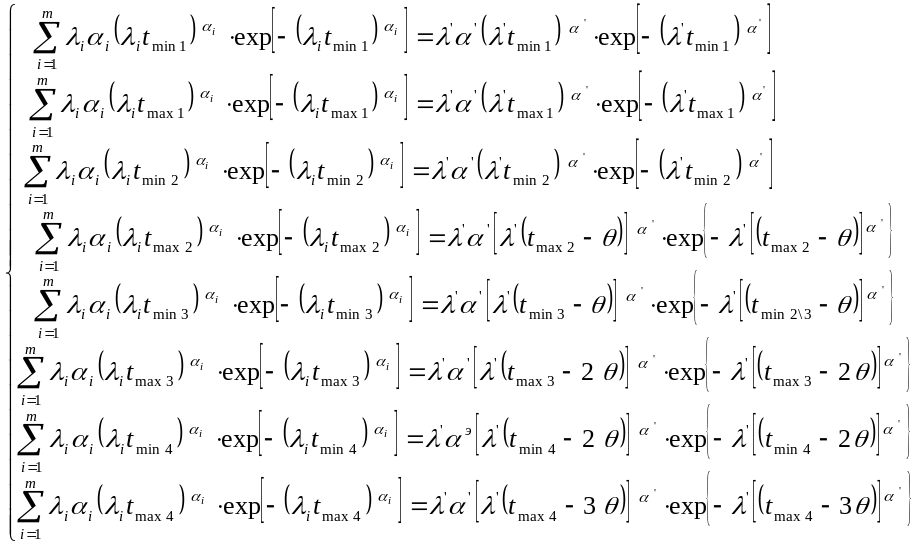 . (4.24)
. (4.24)
Из системы (4.24) получаем следующую систему для нахождения параметров синтезируемой мкльтисерверной системы:
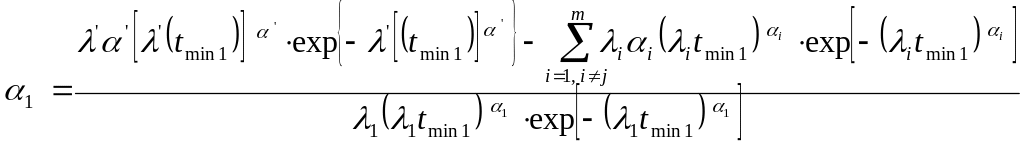 ;
;
 ;
;
 ;
;
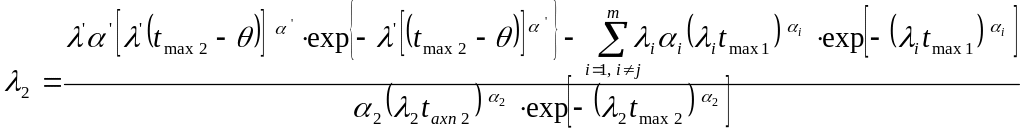 ;
;
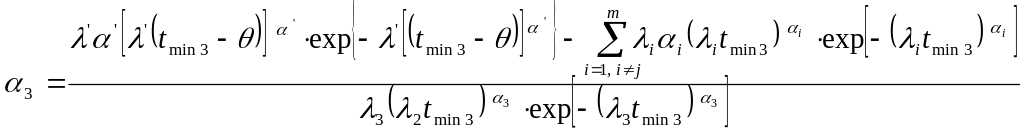
И так далее. Если задано -е приближение , , то -е приближение находим по формулам [6]:
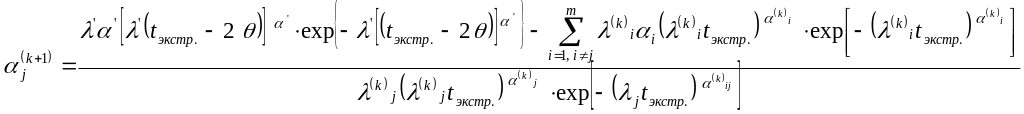
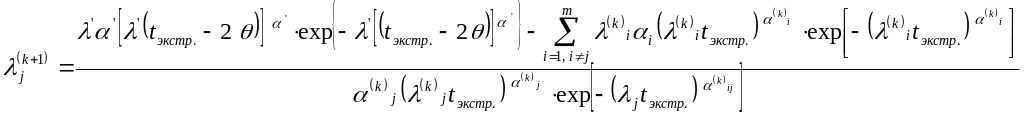
Получена методика нахождения параметров функций риска для компонентов синтезируемой МСС по заданным параметрам общей функции риска и диапазона предельно допустимого ущерба. Учтено, что при задании требуемого вида общего риска системы количество максимумов должно быть равно количеству компонентов, включенных в систему. Показана эффективность метода уравнивания в точках экстремумов значений искомой общей функции риска со значениями заданной функции риска в тех же точках. Важно, что данный метод позволяет не только получать необходимые параметры компонентов системы, обеспечивающих требуемый вид общей функции риска, график которой колеблется в заданной полосе неравномерности, но и не выходить за пределы заданного диапазона ущербов. Полученные оценки параметров позволят заранее оценивать ущербы от нахождения системы в режиме отказа в обслуживании и принять эффективные управленческие решения по оптимизации риска МСС.
Данная методика носит достаточно общий характер и применима и в тех случаях, когда функция плотности вероятности наступления ущерба задана другими гладкими функциями двухпараметрических распределений. При использовании данной методики сняты существенные ограничения на параметры ее компонентов, заключающиеся в уравнивании пиковых значений функций рисков, что ранее активно использовалось при получении параметров компонентов систем. Полученные оценки параметров позволят заранее оценивать ущербы от нахождения системы в режиме отказа в обслуживании и принять эффективные управленческие решения по оптимизации риска МСС. Предложенный метод позволяет найти параметры функций риска компонентов системы таким образом, чтобы обеспечить балансировку загрузки серверов, а это, в свою очередь, позволит при реализации инновационных проектов, носящих распределенный характер, будет способствовать эффективному использованию вычислительной техники.
