
- •Математика Пособие для подготовки к егэ в 2 частях
- •Часть 2
- •11 Кафедра теоретической гидрометеорологии вунц ввс "вва";
- •Введение
- •Свойства логарифмов
- •1.3. Тождественные преобразования показательных и логарифмических выражений
- •Задачи для самостоятельного решения
- •1.4. Показательные уравнения
- •Задачи для самостоятельного решения
- •1.5. Показательные неравенства
- •Задачи для самостоятельного решения
- •1.6. Логарифмические уравнения
- •Задачи для самостоятельного решения
- •1.7. Логарифмические неравенства
- •Задачи для самостоятельного решения
- •1.8. Системы показательных и логарифмических уравнений и неравенств
- •Задачи для самостоятельного решения
- •2. Задачи с параметрами
- •Задачи для самостоятельного решения
- •3. Геометрия
- •3.1. Основные формулы
- •Радианное и градусное измерение углов
- •Заключение
- •Библиографический список
- •Оглавление
- •Математика
- •Часть 2
- •3 94006, Воронеж, ул. 20-летия Октября, 84
Свойства логарифмов
1º.
Логарифм основания равен единице:
![]()
2º.
Логарифм единицы равен нулю:
![]()
3º.
Основное логарифмическое тождество:
![]()
4º.Формула для логарифма произведения:
![]()
5º. Формула для логарифма частного:
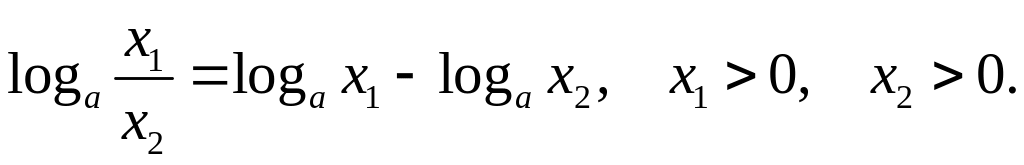
6º.
Формула для логарифма степени:
![]() .
.
7º.
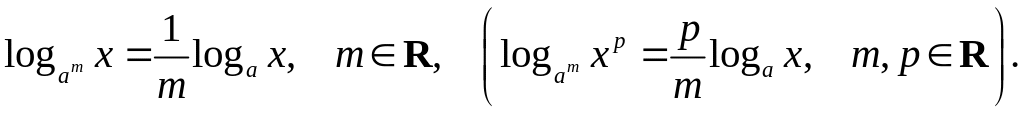
8º.
Формула перехода к новому основанию:

9º.

1.3. Тождественные преобразования показательных и логарифмических выражений
Пример
1.
Вычислить:
![]() .
.
Используя свойства степеней и логарифмов, получим
![]()
Пример
2.
Вычислить:
![]() .
.
Используя свойства логарифмов (3, 9), получим
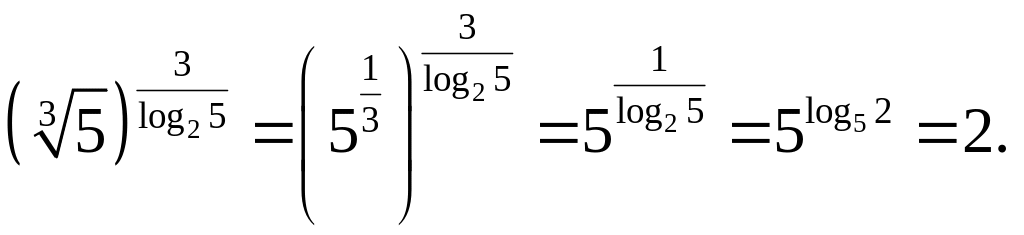
Пример
3.
Вычислить
![]() если
если
![]()
Используя свойства логарифмов, получим
![]() Пусть
Пусть
![]() тогда
тогда
![]() Далее имеем
Далее имеем

По
условию
![]() тогда получим уравнение
тогда получим уравнение
![]()
![]()
тогда
![]()
Часто приходится прологарифмировать обе части данного выражения или, напротив, потенцировать. Логарифмирование – это такое преобразование, при котором логарифм выражения с переменными приводится к сумме или разности логарифмов переменных. Потенцирование – это действие, обратное логарифмированию.
Пример
4.
Дано
![]() Найти
Найти
![]()
Логарифмируя обе части равенства, получим
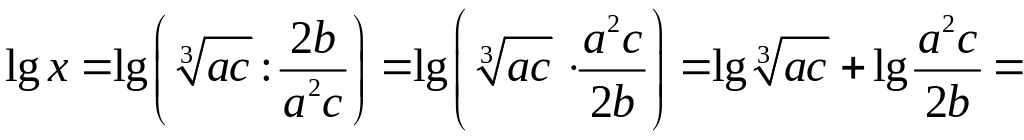
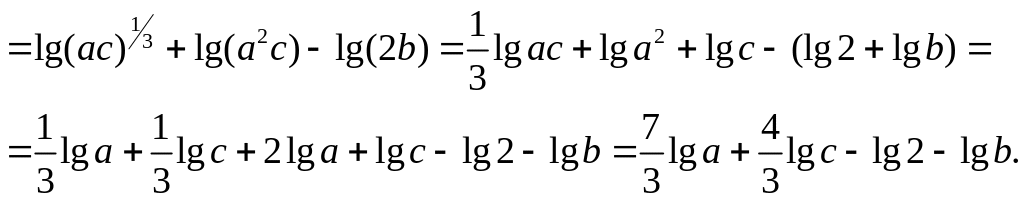
Пример
5.
Найти
по данному его логарифму:
![]()
Потенцируя обе части равенства, получим
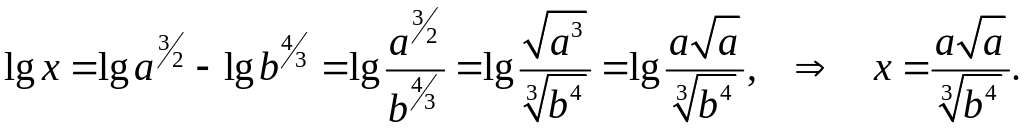
Задачи для самостоятельного решения
Вычислить:
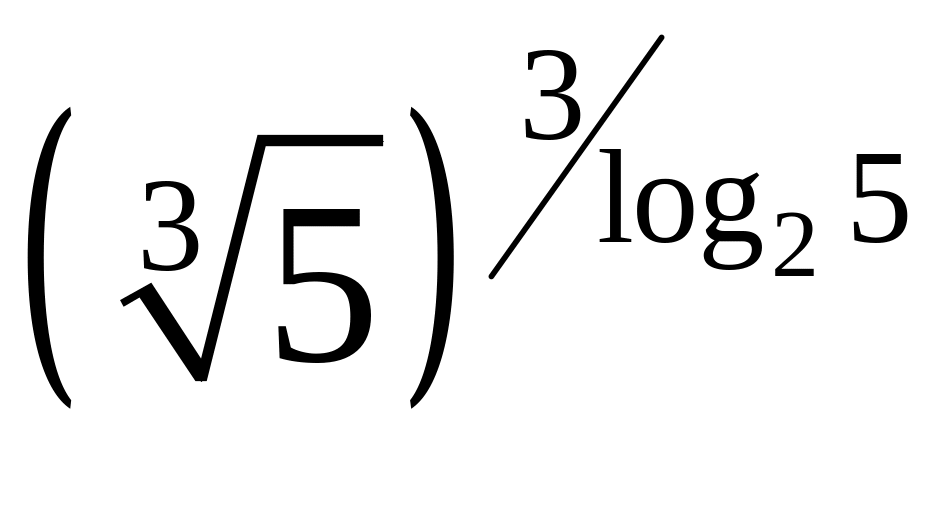 ;
2)
;
2)
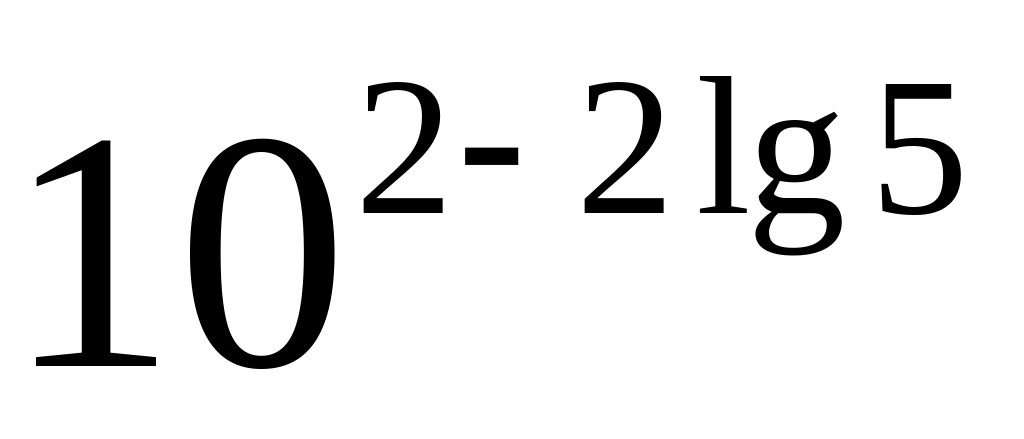 ;
3)
;
3)
 ; 4)
; 4)
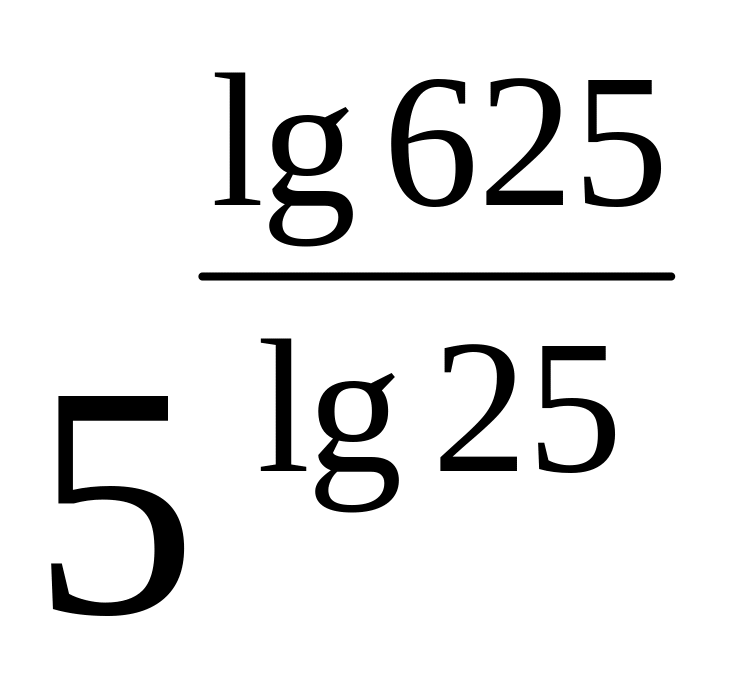 ;
;
5)
 6)
6)
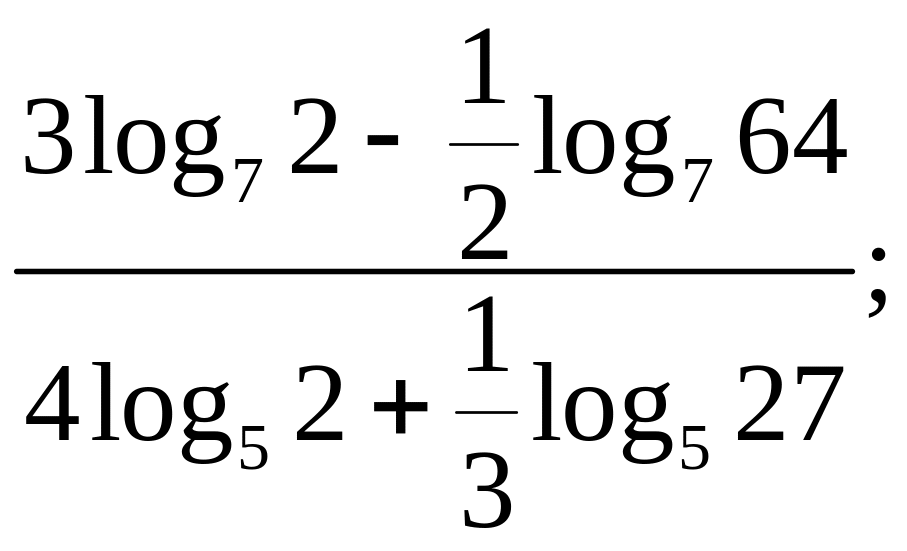
7)
![]() 8)
8)
![]()
9)
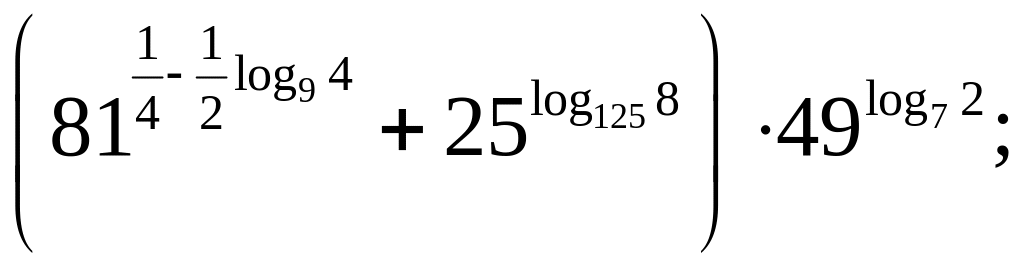 10)
10)
![]()
11)
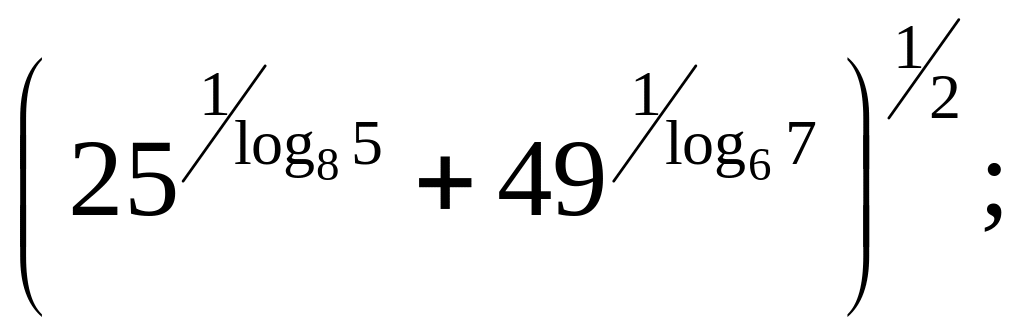 12)
12)
![]()
13)
![]() 14)
14)
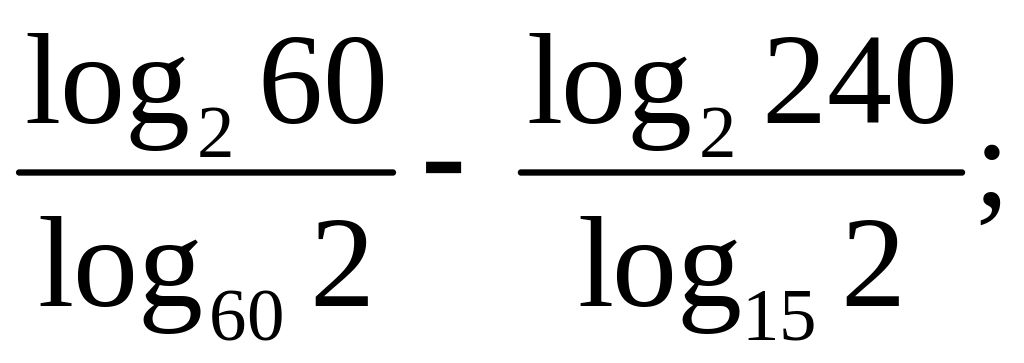
15)
![]() 16)
16)
![]()
17)
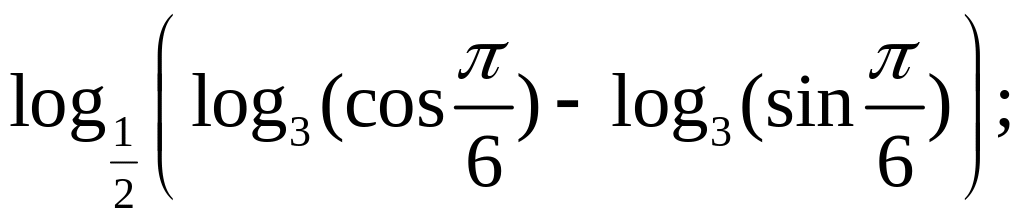 18)
18)
![]()
19)
![]() 20)
20)
![]()
21)
![]() 22)
22)
![]()
23)
![]() 24)
24)
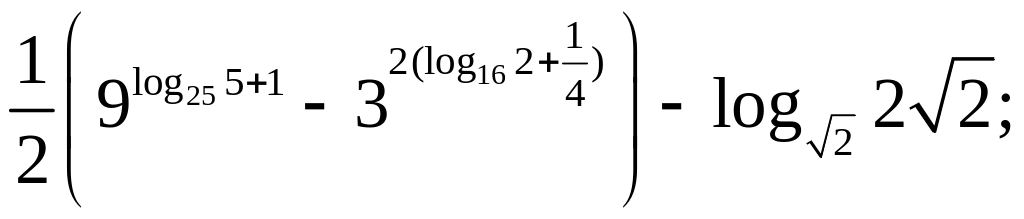
25)
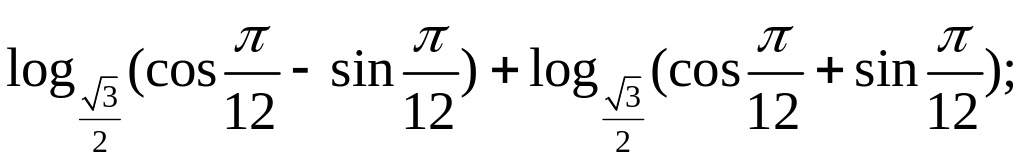 26)
26)
![]()
27)
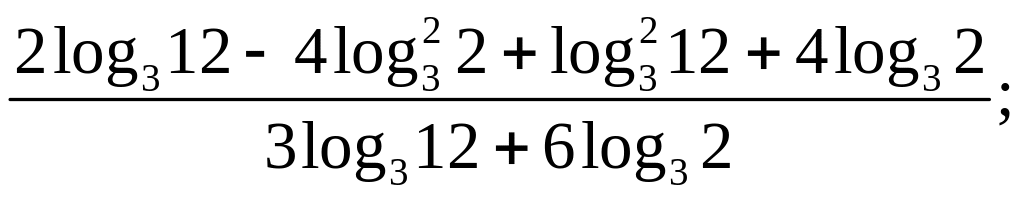
28)
![]() 29)
29)
![]()
30)
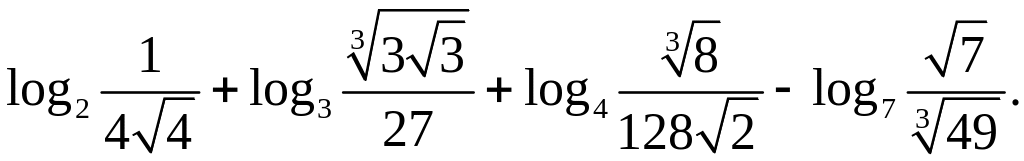
1.4. Показательные уравнения
Уравнение, содержащее переменную в показателе степени, называется показательным.
Решение
показательных уравнений часто сводится
к решению уравнения вида
![]() где
где
![]()
Основные приёмы решения показательных уравнений разберём на следующих примерах.
Пример
1.
Решить уравнение

Используя свойства степеней, приведем левую и правую части уравнения к одному основанию:
 откуда
откуда
![]() Поскольку функция
Поскольку функция
![]() монотонна и каждое свое значение
принимает ровно один раз, то последнее
уравнение равносильно уравнению
монотонна и каждое свое значение
принимает ровно один раз, то последнее
уравнение равносильно уравнению
![]() из которого находим
из которого находим
![]()
Пример
2.
Решить уравнение
![]()
Вынесем
за скобку
![]() – степень с наименьшим показателем:
– степень с наименьшим показателем:
![]() откуда
откуда
![]() или
или
![]()
Пример
3.
Решить уравнение
![]()
В
левой части уравнения вынесем за скобку
![]() ,
а в правой части вынесем за скобки
,
а в правой части вынесем за скобки
![]()
![]()
Поделим
обе части последнего уравнения на
![]() ,
получим
,
получим
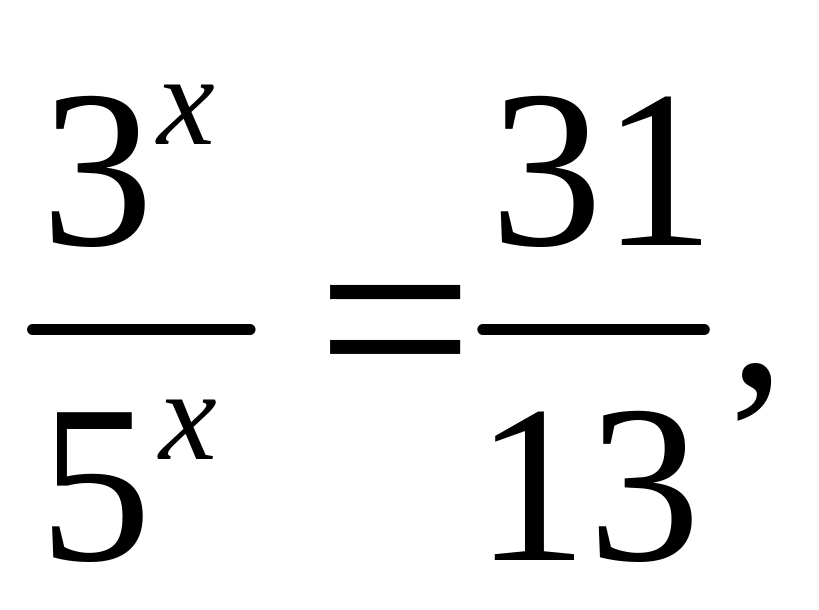 или
или
 откуда, логарифмируя обе части уравнения
по основанию
откуда, логарифмируя обе части уравнения
по основанию
![]() (можно по любому положительному
основанию), получим
(можно по любому положительному
основанию), получим
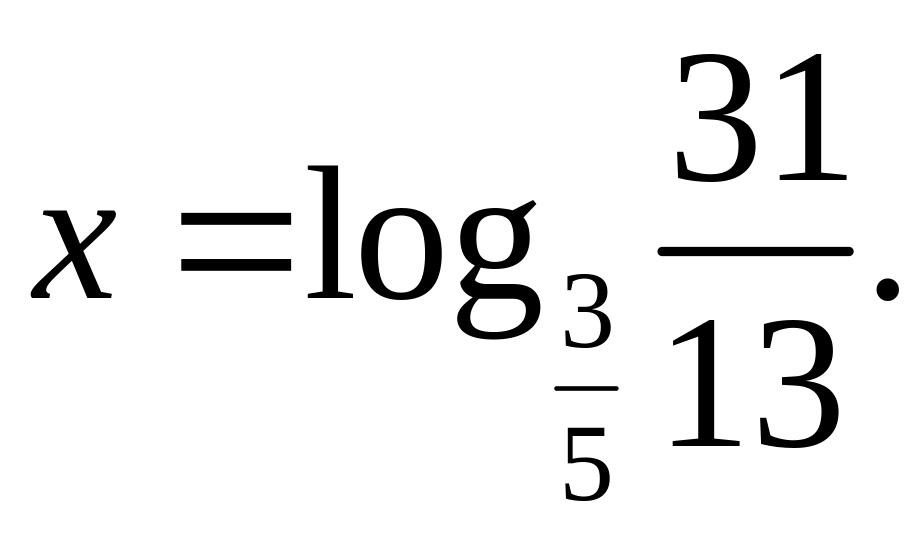
Пример
4.
Решить уравнение
![]()
Используя свойства степеней, преобразуем исходное уравнение к виду
![]() Полученное
уравнение удобнее всего решать, введя
новую переменную
Полученное
уравнение удобнее всего решать, введя
новую переменную
![]() Тогда уравнение сводится к квадратному
относительно новой переменной
Тогда уравнение сводится к квадратному
относительно новой переменной
![]() :
:
![]() решая
которое, находим
решая
которое, находим
![]() Корень
Корень
![]() не удовлетворяет условию
не удовлетворяет условию
![]() ,
поэтому единственное решение исходного
уравнения определяется из соотношения
,
поэтому единственное решение исходного
уравнения определяется из соотношения
![]()
Пример
5.
Решить уравнение
![]()
Запишем
исходное уравнение в виде
![]()
Это
однородное уравнение второй степени.
Разделим обе части уравнения на
![]() ,
получим
,
получим
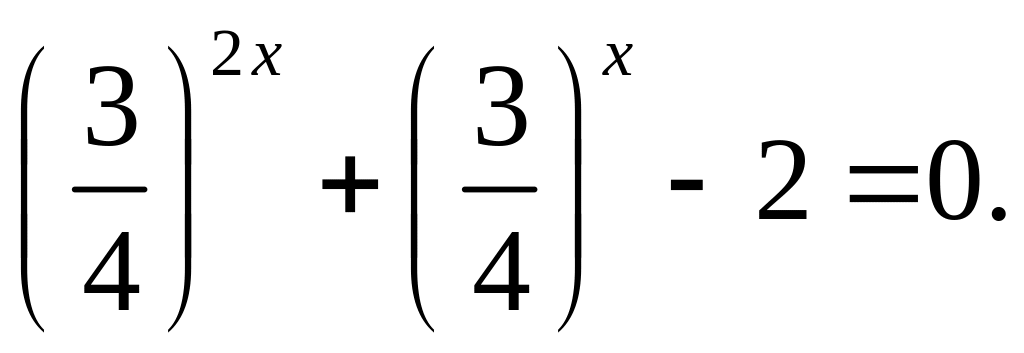
Введем
новую переменную
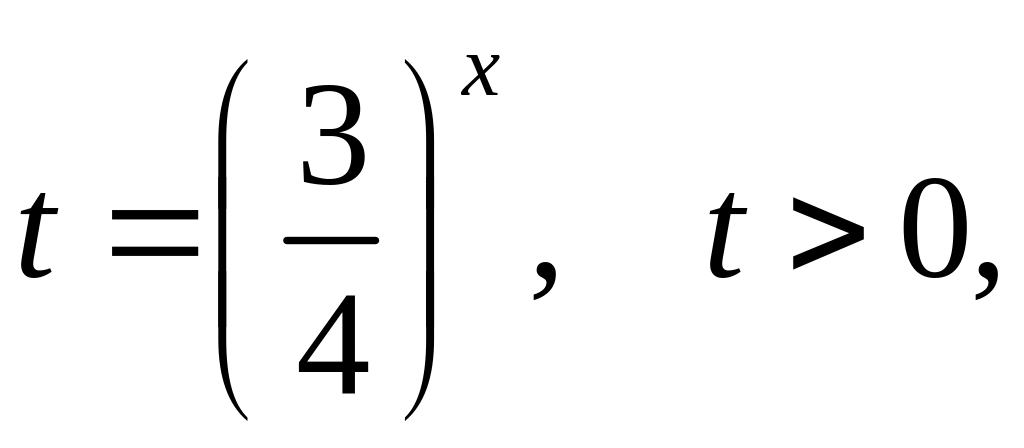 придем к квадратному уравнению
придем к квадратному уравнению
![]() решив
которое, найдем
решив
которое, найдем
![]() Второй корень не удовлетворяет условию
Второй корень не удовлетворяет условию
![]() Возвращаемся к исходной переменной,
получаем уравнение
Возвращаемся к исходной переменной,
получаем уравнение
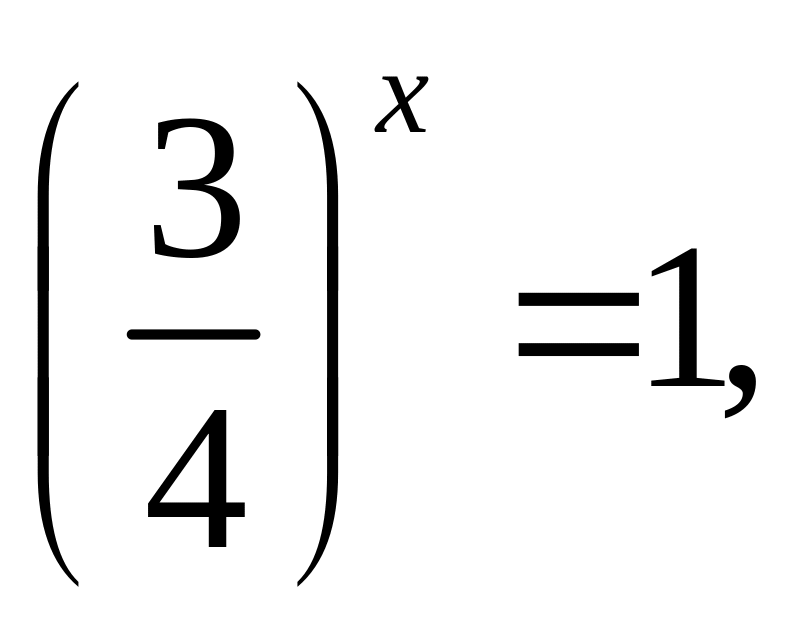 откуда
откуда
![]()
Пример
6.
Решить уравнение
![]()
Числа
![]() и
и
![]() являются взаимно обратными:
являются взаимно обратными:
![]()
Введем
новую переменную
![]() Тогда исходное уравнение примет вид
Тогда исходное уравнение примет вид
![]() или
или
![]() Корни последнего уравнения равны
Корни последнего уравнения равны
![]() откуда
откуда
![]()
Пример
7. Решить
уравнение
![]()
Прологарифмируем данное уравнение по основанию 5 (или 2). Следует заметить, что можно, вообще говоря, логарифмировать по любому основанию, но не совсем удачный выбор основания может привести к громоздким вычислениям.
Имеем
![]() или
или
![]()
![]()
![]()
![]()
![]()
Пример
8. Решить
уравнение
![]()
Легко
заметить, что
![]() является корнем данного уравнения.
Докажем, что других корней данное
уравнение не имеет. Для этого разделим
левую и правую части уравнения на
является корнем данного уравнения.
Докажем, что других корней данное
уравнение не имеет. Для этого разделим
левую и правую части уравнения на
![]() .
Получим
.
Получим

Функция, стоящая в левой части последнего уравнения, монотонно убывающая (основание степени меньше единицы), а функция, стоящая в правой его части, монотонно возрастает. Поэтому уравнение не может иметь более одного решения. Таким образом, единственное решение.
Пример
9. Решить
уравнение
![]()
Возможны
случаи: 1)
![]() т.е.
т.е.
![]() тогда получим
тогда получим
![]() верное
равенство, значит,
верное
равенство, значит,
![]() –
корень данного уравнения;
–
корень данного уравнения;
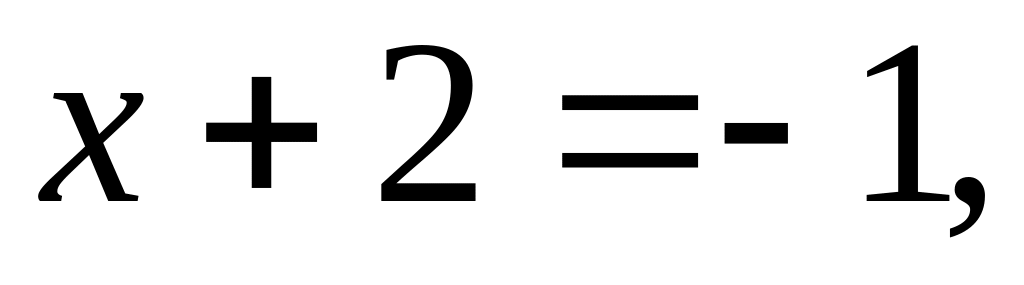 т.е.
т.е.
 тогда уравнение примет вид
тогда уравнение примет вид
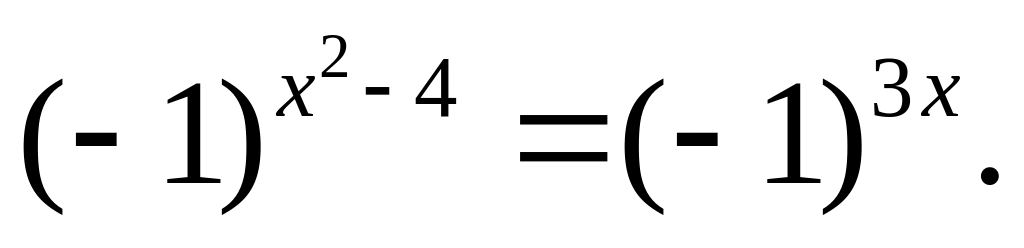
Этому
уравнению могут удовлетворять только
те значения
,
при которых
![]() и
и
![]() целые числа (так как число
целые числа (так как число
![]() можно возводить лишь в целую степень)
одинаковой четности, т.е. либо оба четные,
либо оба нечетные.
можно возводить лишь в целую степень)
одинаковой четности, т.е. либо оба четные,
либо оба нечетные.
При
![]() имеем
имеем
![]() верно,
значит,
–
корень данного уравнения.
верно,
значит,
–
корень данного уравнения.
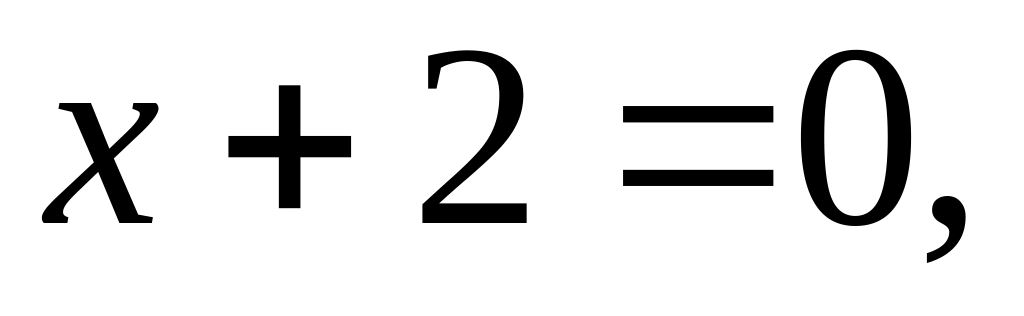 откуда
откуда
 В этом случае исходное уравнение имеет
вид
В этом случае исходное уравнение имеет
вид
![]() и
так как выражение
и
так как выражение
![]() имеет смысл лишь при
имеет смысл лишь при
![]() ,
то значение
,
то значение
![]() не подходит, а следовательно не является
корнем данного уравнения.
не подходит, а следовательно не является
корнем данного уравнения.
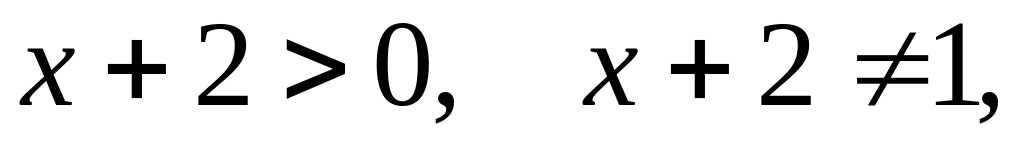 то
из данного уравнения имеем
то
из данного уравнения имеем
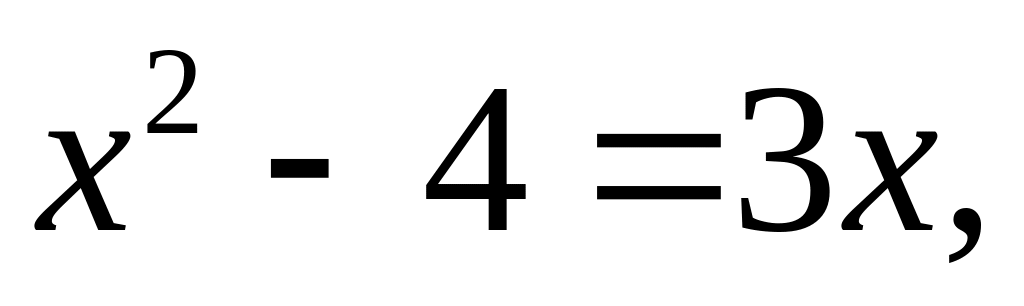 откуда
откуда
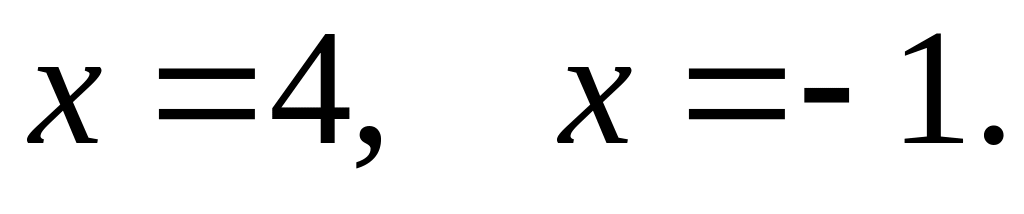
При
![]() получим
получим
![]() верное
равенство. Значит
– корень исходного уравнения. При
получим
верное
равенство, значит
– корень уравнения.
верное
равенство. Значит
– корень исходного уравнения. При
получим
верное
равенство, значит
– корень уравнения.
Итак
данное уравнение имеет 3 корня:
![]()
Пример
10.
Решить уравнение
![]()
Данное уравнение равносильно совокупности
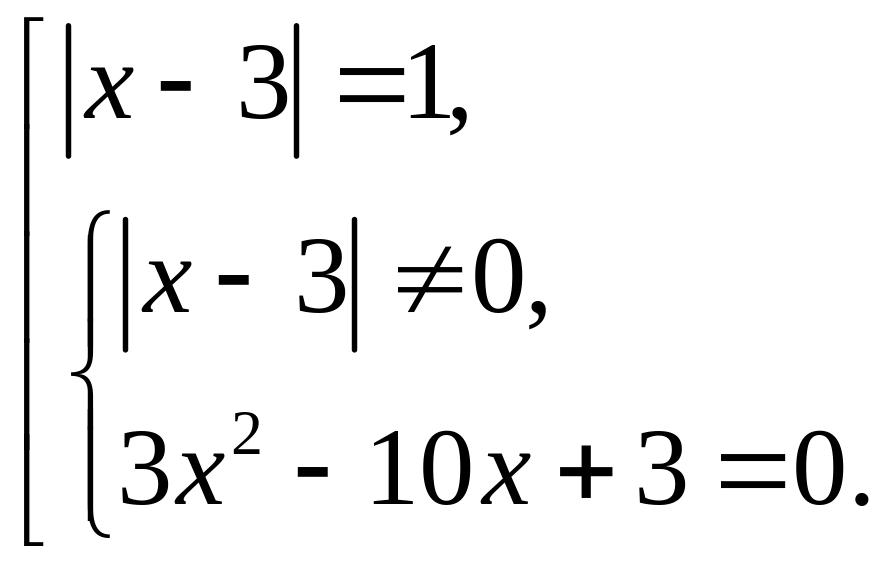
Из
первого уравнения получаем
![]() Из системы находим
Из системы находим
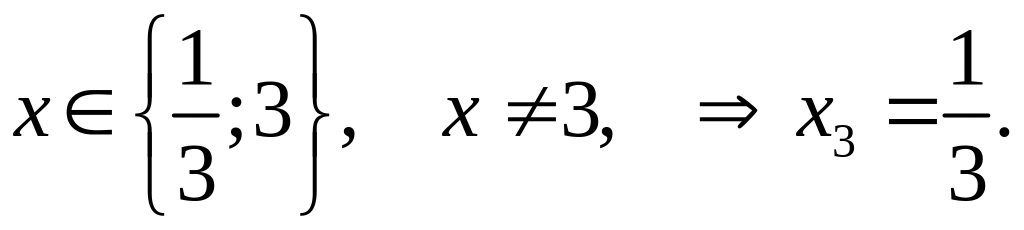
Т.е.

