Распишем уравнение относительно рисков:

Аналогично получим решение относительно противодействующих параметров:

(3.31)

Продифференцируем одно уравнение и подставим в него другое:

(3.32)

(3.33)

Полученное выражение является уравнением гармонического осциллятора с периодом .

Рассмотрим систему как замкнутую и обладающую свойством робастной устойчивости по отношению к неопределенности внешних воздействий (рисков). Схем реализации процесса в такой постановке задачи представлена на рис. 3.11 [85, 86, 105].

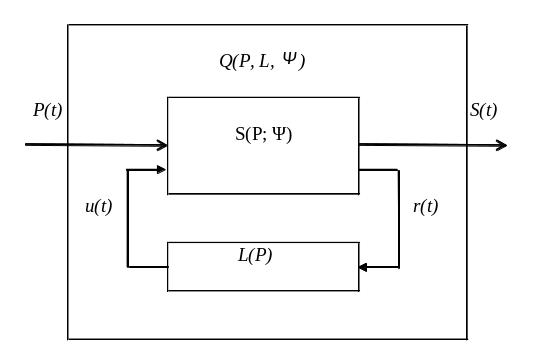
Рис. 3.11. Схема работы экономической системы под воздействием

возмущающих параметров.

На рис. 3.11 приняты следующие обозначения: S(P; Ψ), L(P), Q(P; K; Ψ) – передаточные матрицы объекта, регулятора и замкнутой системы соответственно. Символом Ψ обозначена передаточная матрица той части объекта, которая представляет неопределенность в задании его математической модели.

Предположим, что замкнутая система Q(P; L; Ψ) обладает свойством робастной устойчивости по отношению к неопределенности Ψ (P). В этом случае будем говорить, что регулятор u=L(P)r обеспечивает робастную устойчивость замкнутой системы [85, 105].

Проиллюстрируем понятие робастной устойчивости для систем с неструктурированными неопределенностями (не моделируемой динамикой). На примере объекта инвестиционного управления со скалярными входом u и выходом y, которые связаны между собой уравнением

, (3.34)

где – номинальная передаточная функция. Объект с математической моделью (3.34) стабилизируется регулятором

, (3.35)

где L(P) - передаточная функция системы (3.34, 3.35).

С целью формализации дальнейшего рассмотрения проблемы, введем ряд понятий, позволяющих количественно характеризовать возмущения математических моделей. Предположим, что передаточная функция L(P) регулятора не изменяется в процессе функционирования, а передаточная функция объекта подвергается воздействию неструктурированных возмущений непараметрического типа. В результате подобного воздействия, регулятор (3.35) фактически замыкает не объект с моделью (3.34), а другой объект

, (3.36)

передаточная функция которого отличается от номинальной .

В связи с наличием указанной неопределенности неструктурированного типа, возникают два естественных вопроса, ответы на которые позволяют оценивать качество стабилизирующего регулятора (3.35) в плане допустимости неконтролируемых вариаций математической модели объекта:

• будет ли сохраняться устойчивость системы при условии, что возмущение передаточной функции объекта находятся в заданных границах;

• каковы предельно допустимые границы изменения возмущений, которые не приводят к потере устойчивости.

Поставленные вопросы относятся к области анализа меры робастной устойчивости динамических систем. Определим показатель Ψ(P) абсолютного возмущения модели (или возмущения номинальной передаточной функции ):

. (3.37)

Соответственно, относительным возмущением модели или номинальной передаточной функции будем называть рациональную дробь

. (3.38)

Взвешенным относительным возмущением модели или номинальной передаточной матрицей (или просто возмущением либо неопределенностью) будем считать

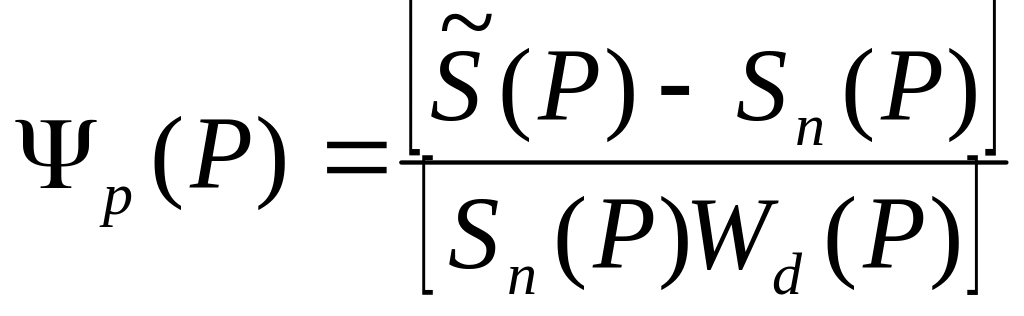, (3.39)

где  – это заданная весовая дробно рациональная функция.

Введение весовой функции в определение возмущения (3.39) модели обусловлено амплитудно-частотными характеристиками (АЧХ) и для номинального и возмущенного объектов соответственно.

Введем допустимую границу возмущения номинальной математической модели, определяя ее ограничением сверху (для каждой частоты) величины модуля относительного изменения АЧХ положительным числом (это число можно считать заданным в %). Иными словами, введение функции определяет условие

, (3.40)

задающее допустимый «коридор» для вариаций АЧХ фактического (возмущенного) объекта (3.34), что изображено на рис. 3.12.

Рис.3.12. Допустимый «коридор» для вариаций АЧХ

фактического (возмущенного) объекта

Таким образом, функция частоты  – это относительная ширина допустимого коридора для АЧХ возмущенного объекта. Заметим, что работать аналитически с условием (3.39) не вполне удобно. Вместо него можно использовать соотношение вида

, (3.41)

которое является более сильным, чем (3.41), что следует из неравенства

, (3.42)

справедливого для любых двух комплексных чисел S и S_n. Таким образом, выполнение (3.41) влечет за собой выполнение (3.40).

Итак, если задано дробно-рациональное выражение и для всех передаточных функций объектов с возмущенными моделями выполняется условие (3.41), то согласно (3.38) будет выполняться неравенство

, (3.43)

то есть АЧХ относительного возмущения модели не выйдет за пределы области допустимого возмущения.

Кроме того, согласно формуле (3.39), для АЧХ взвешенного относительного возмущения Ψ_P модели объекта будет выполняться неравенство

, (3.44)

которое можно трактовать, как нормированное ограничение на допустимые вариации линеаризованной модели.

Таким образом, представляется возможным определить «коридор» значений прогнозируемых параметров. Экономически это будут предельные значения влияния факторов как внешних, так и внутренних на результат реализации проекта. Условия нестабильности экономической системы могут быть определены количественно с условиями предельно допустимых отклонений, что дает возможность прогнозирования результатов процесса, подвергаемого непараметрическим воздействиям.

Рассмотрим реализацию модели оценки устойчивости на исследуемом процессе. В данном случае, при адаптации к работе реального объекта, система может быть представлена как совокупность реализаций внутри фазового пространства, верхняя граница которого определена функцией максимальной прибыли без учета рисков, а нижняя – функцией прибыли с максимальным уровнем риска. Границы определены функциями:

f_max(x) = -18,55x² +1330,1x - 0,96, (3.45)

f_min(x) = -16,08х² +990,41х +226,24 (3.46)

Система описывается линейными дифференциальными уравнениями.

Для устойчивости линейного дифференциального уравнения n-го порядка с постоянными коэффициентами необходимо и достаточно, чтобы корни характеристического уравнения имели неположительные вещественные части, причем корни с нулевой вещественной частью должны быть простыми. Графически коридор вариаций представлен на рис. 3.13.

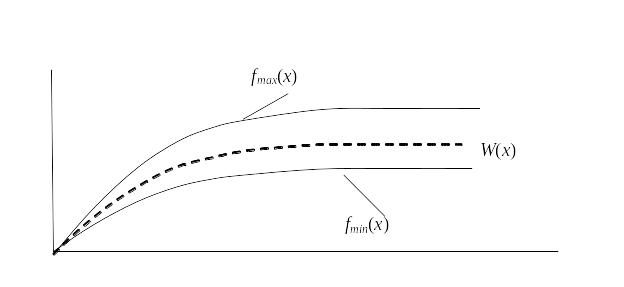
Рис.3.13. Коридор вариаций параметров системы.

В соответствии с рис. 3.13

˂ (3.47)

На основании (3.45) и (3.46) получим:

-16,08х² +990,41х +226,24 ˂ -18,55x² +1330,1x - 0,96 (3.48)

Решая квадратное неравенство, получим интервал значений [0,67; 136]. Если х – количество этажей высотного объекта, то в данном случае реализация будет эффективна на указанном интервале значений.

Функция частоты  – это относительная ширина допустимого коридора для АЧХ возмущенного объекта.

Р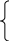 ешая систему уравнений

= -16,08х² +990,41х +226,24

= -18,55x² +1330,1x - 0,96,

получим значение функции W(x), являющееся границей интервала [ , определяющее центральное положение прогнозной линии относительно коридора варьирования:

W(x)= -1,2х²+169,9х-113,6.

Метод позволяет конструировать прогнозные значения исследуемых параметров при заданном коридоре вариаций признака.