6.15. Потоковые задачи

Нам потребуются новые понятия. Разрезом называют разбиение множества узлов связного графа на 2 непустых подмножества VI, V2, а сечением - множество дуг, одновременно инцидентных узлу из VI и узлу из V2. Удаление всех этих дуг превращает граф в несвязный.

Сеть - это связный орграф с выделенными узлами - полюсами. Транспортная сеть имеет 2 полюса: исток s и сток t; в s не входя? дуги, а из t дуги не выходят. Это взвешенный граф, ибо каждой дуге е поставлена в соответствие пропускная способность с(е). Поток по дуге -J количество вещества, проходящего по дуге за единицу времени, оно не больше с(е). В узлах вещество не производится (кроме узла s) и не накапливается, поэтому суммарные потоки по дугам, входящим в узел, и дугам, выходящим из узла, равны. Величина потока - это сумма потоков по дугам, входящим в t, или по дугам, выходящим из s. Дугу, направление которой совпадает (не совпадает) с направлением движения от s к t, называют прямой (обратной).

Разрез транспортной сетитаков, что s принадлежит VI, t - V2, причем обязательно найдется такое сечение, что сумма с(е) по его прямым дугам минимальна. Эта сумма равна максимально возможному потоку F_max. Соответствующий разрез называют минимальным.

В изображенной ниже транспортной сети G3 пропускная способность дуг напечатана жирно, а рядом - поток по дуге. Узлы обозначены латинскими буквами. Сечение минимального разреза показано двойными линиями.

Обратите внимание на то, что при максимальном потоке все прямые дуги сечения насыщены, т. е. поток f(e) в них равен е(е), а поток f(e) в обратных дугах сечения равен нулю. Получение F_max – процесс итерационный; начальным приближением может быть любой поток, хотя бы и равный нулю в каждой дуге.

Доказано [11], что можно ограничиться рассмотрением кратчайших цепей <s → t> в процессе увеличения потока, но эти цепи строятся не только из прямых, но и из обратных дуг, и всякий раз поток в цепи увеличивается либо до насыщения какой-либо прямой дуги цепи, либо до сведения к нулю потока в обратной дуге цепи, смотря что из этих событий раньше осуществится. В дальнейшем прямые насыщенные дуги или обратные дуги с нулевым потоком исключа­ются, поэтому имеется тенденция роста длины выявляемых кратчай­ших цепей, а на каком-то шаге (итерации) никакую цепь, ведущую от s к t, построить не удается. Это и будет признаком получения максимального потока.

Метод, использующий идеи Форда и Фалкерсона, Эдмондса и Карпа [10], предполагает рассмотрение не более m n/2 цепей, а сложность его - О(m² • n), т. е. довольно высока: для графов большой полноты она приближается к О(n⁵). Понятно, это вызвано перебором много­численных цепей и узлов в каждой цепи. Реализованы улучшения метода за счет использования специальных структур [10], сокращаю­щие перебор и приводящие к оценке О(n³).

Ниже рассматривается не публиковавшийся ранее простой алгоритм; в нем каждая итерация включает поиск в ширину, который приме­нялся и прежде для нахождения кратчайших цепей, и поиск в глуби­ну в подграфе, содержащем все узлы множества кратчайших цепей.

Поиск в ширину - это 1-я фаза каждой итерации и нужен он лишь для того, чтобы упорядочить узлы по ярусам широтного каркаса (см. п. 5.9). Фактическое построение кратчайших цепей и их анализ про­исходит на 2-й фазе методом поиска в глубину, сокращающего пере­бор узлов за счет совмещенной обработки "стволов" - пересечений цепей, являющихся началом цепей *, и отбрасывания ветвей, не тре­бующих рассмотрения.

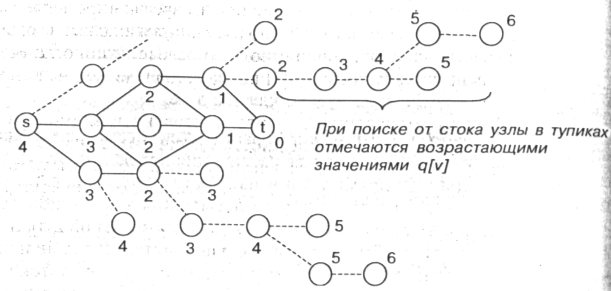
Поиск в ширину начинаем необычно - от стока t, и вот почему: движение на 2-й фазе надо ограничить "рельсами" кратчайших пу­тей. Проходить тупики нам ни к чему. Изучите следующий рисунок. При поиске в ширину от истока s, мы получили бы "бахрому" тупиков, изображенную пунктиром, и бродили по этим тупикам на 2-й фазе. Тупики не исчезнут при поиске от стока t, но поиск в глубину их не затронет, ибо движение на 2-й фазе разрешено лишь в сторону убывания номера яруса q [v] (см. цифры возле узлов).

Рассмотрим 2-ю фазу. Пусть конечный узел ствола занимает в стеке 3 позицию. В элементе U[3] будет запоминаться "узкое место" данного ствола, т.е. входящая в него прямая дуга с минимальной разностью о[3] = с(е) - f(e), либо обратная дуга с минимальным потоком! о[3] = f(e), смотря что из них меньше. "Узкое место" удлиненного! ствола может быть тем же или лежит в приращении ствола. Исходя ; из этого, находим и запоминаем следующие значения U[k], o[k] при ' продвижении по цепи <s → t>.

Заметим, что факт "произрастания" из ствола очередной цепи обна­руживается в момент возврата - по другой цепи - к концу ствола; именно поэтому U[k], o[k] надо хранить. Следующий рисунок пояс­няет ситуацию на момент завершения семизвенной цепи < -5 → 10>; дуга е - "узкое место" в ней вычерчена жирно. Эта дуга насыщается при увеличении потока во всех дугах цепи на величину о[8] (сток занимает 8-ю позицию в стеке). Штриховым контуром ограничен подграф; в нем 6 четырехзвенных цепей, ведущих от е к t, и 5 из них не рассматриваются ввиду исключения насыщенной дуги е: возврат j от cтока t ведет в ее начало - узел 6, где востребуются U[3], o[3]. При возврате в 4 звеньях цепи поток. f[v] возрастает на величину о[8]. Затем начинается движение "вперед" по новой цепи, к узлу 4 и 1 далее

П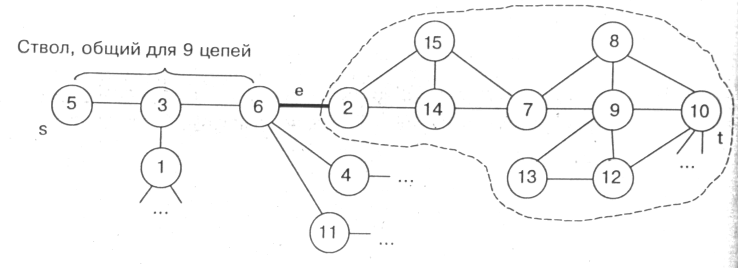 ри возвратах по стволам экономим время: в элементе D[k] аккумулируем увеличения потока по результатам анализа всех цепей, "про­израстающих" из конца ствола; впоследствии, когда возвращаемся по стволу, увеличиваем f[v] в дугах ствола один раз.

Максимум значения k – это n, столько и элементов U[k] (o[k], D[k]), т. е. емкостная сложность увеличивается на 3n. Это недорогая цена. В [10] предлагается вспомогательная сеть и затраты памяти для нее соизмеримы с затратами на описание исходной сети.

Предлагаемый алгоритм реализует блок Potok, приводимый ниже.

Пример 6.14.

Применим блок Potok к сети G3 (изображена выше).

Const n=12; {Предел значения n равен 127}

Type matr = array[1..n,1..n] of word; mas=array[1..n] of word;

Const p:matr = ((0, 4, 0, 7, 2, 0, 0, 0, 0, 0, 0, 0), {a}

(0, 0, 0, 0, 0, 7, 0, 0, 3, 0, 0, 0), {b}

(0, 0, 0, 0, 0, 8, 2, 0, 0, 0, 0, 0), {c}

(0, 0, 0, 0, 8, 0, 0, 2, 0, 0, 0, 0), {d}

(0, 0, 0, 0, 0, 0, 0, 6, 0, 6, 0, 0), {e}

(5, 0, 0, 0, 0, 0, 11, 0, 0, 0, 0, 0), {f}

(0, 0, 0, 0, 0, 0, 0, 0, 0, 12, 0, 2), {g}

(0, 0, 0, 0, 0, 0, 0, 0, 3, 0, 0, 9), {h}

(0, 0, 0, 0, 0, 3, 0, 0, 0, 8, 0, 3), {i}

(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 15), {j}

(6, 10, 14, 0, 0, 0, 0, 0, 0, 0, 0, 0), {s}

(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)); {t}

Var f:matr; v2:mas; i,j,nf,mf: word;

Procedure POTOK(s,t:word; Var nf,mf:word; Var p,f:matr; Var o:mas);

Var D,st,U,q: mas; a, c, dd, i, ii, j, k, kk, l, min: word;

Function Shir: Boolean; {Блоквычисления q[L], где L - номерузла}

Begin j:=1; Repeat q[j]:=n; j:=j+1 Until j > n; q[t]:=0;

Shir:= true; o[1]:=t; k:=1; i:=1; c:=0;

Repeat ii:=k; c:=c+1;

Repeat j:=o[i]; L:=0;

Repeat L:=L+1; If q[L]=n Then

{Проверяется не насыщенность прямой дуги/наличие потока в обратной) lf(p[L,j]>f[L,j])Or(f[j,L] >0)Then

Begin k:=k+1; o[k]:=L; q[L]:=c;'lf L=sThen Exit End

Until L = n; i:=i+1 {Рассмотрены узлы, смежные с L-м узлом}

Until i > ii {Пройден очередной ярус широтного каркаса}

Until i > k; {Поиск завершен; узел s не встретился}

Shir:= false {Функция Shir получает значение false, ибо}

End; {исток s оказался недостижим}

Procedure Glub; {Поиск в глубину от узла s в направлении убывания q[i]} Procedure pp; {Блок изменения потока в дуге при возврате по ней}

Begin kk:=k; dd:=dd+d[k]; k:=k-1; j:=L;

If k = 0 Then Exit; L:=st[k];

If dd > 0 Then If p[L,j] > 0 Then f[LJ]:=f[L,j]+dd

Else {обратнаядуга} f[j,L]:=f[j,L]-dd

End {блока изменения потока в дуге},

Begin min:=2*Maxlnt; o[1]:=min; U[1]:=1; d[1]:=0;

k:=1; kk:=0; st[k]:=s; L:=s; j:=0;

Repeat a:=0;

Repeat j:=j+1; {Цикл поиска дуги для включения ее в цепь}

If j <= n Then If q[j] < q[L] Then

Begin a:= p[L,j] - f[L,j]; If a = 0 Then a;= f[j,L] End

Until (a > 0) Or (j > n);

If j > n Then pp {Цепь не удалось нарастить, поэтому - шаг назад}

Else {Продвижение "вперед" по найденной прямой или обратной дуге}

Begin If k < kk Then {Только что закончились шаги возврата}

Begin i:=U[k]; d[k]~d[k]+dd; dd:=0; min:=o[k]-d[k] End; k:=k+1; st[k]:=j; d[k]:=0; L:=j; If a < min Then Begin min:= a; i:= k End; If j <> t Then Begin o[k]:=min; U[k]:=i; j:=0 End Else {Конеццепи; пошаговыйвозвраткдуге - "узкомуместу":)

Begin dd:=min; Repeat pp Until k<i End

End

End

Until k=0 {He рассмотренных дуг, исходящих из s, не осталось]

End {блока Glub, поочередно рассматривающего кратчайшие цепи};

Begin

While Shir do Glub; {Пока удается "пробиться" к t, строим цепи}

nf:=k; mf:=0; For j:=1 to n do mf:= mf + f[s,j]

End {блокаРОТОК};

BEGIN For i:=1 to n do For j:=1 to n do f[i,j]:=0; {Исходныйнулевойпоток}

Potok(11,12,nf,mf,p,f,v2); Writeln(mf:4); Readln;

END.

Блок Potok находит и минимальный разрез: nf первых элементов i массива v2 указывают узлы множества V2.

Как свидетельствует эксперимент, предложенный компактный алгоритм принадлежит также и к лучшим по производительности, дает максимальный выигрыш на разреженных графах, где он в несколько раз быстрее алгоритма из [10]. Однако при использовании матрицы! смежности его асимптотическая сложность не может быть меньше О(n²). Имеются его реализации с нематричным описанием графа.

Задание 6.15.

Постройте алгоритм сложности О(n), который дополняет массив v2 номерами узлов множества VI, начиная с (nf+l)-й позиции массива.1