посібник зно математика

Наприклад: степінь многочлена дорівнює степеню одночлена ,

тобто 5+5=10.

Дії над многочленами

При додаванні многочленів користуються правилом розкриття дужок: якщо перед дужками стоїть знак «+», то дужки можна опустити, зберігши знаки кожного одночлена.

Наприклад: .

При відніманні многочленів користуються правилом розкриття дужок: якщо перед дужками стоїть знак «-», то дужки можна опустити, змінивши знак кожного одночлена, що містився в дужках, на протилежний.

Наприклад:

.

Щоб записати алгебрагічну суму кількох многочленів як многочлен стандартного вигляду, треба розкрити дужки і звести подібні члени.

Наприклад:

.

Щоб помножити одночлен на многочлен, треба кожний член многочлена помножити на цей одночлен й одержані одночлени додати.

Наприклад: .

Щоб помножити многочлен на многочлен, треба кожний член одного многочлена помножити на кожний член другого многочлена й одержані многочлени додати.

Наприклад:

.

Щоб розділити многочлен на одночлен, треба кожний член многочлена розділити на цей многочлен й одержані результати додати.

Наприклад:

.

Розкладанням многочлена на множники називають запис многочлена у вигляді добутку многочленів.

Наприклад: .

Логарифм числа, властивості логарифмів

Логарифмом додатного числа за основою називається

показник степеня, до якого треба піднести , щоб одержати .

Приклади: , оскільки ;

Десятковий логарифм

Основна логарифмічна тотожність

Приклад:

Властивості і формули логарифмування

1.Логарифм одиниці за будь-якою основою дорівнює нулю

2.Логарифм добутку додатних чисел дорівнює сумі логарифмів множників

3.Логарифм частки додатних чисел дорівнює різниці логарифмів діленого і дільника

4.Логарифм степеня додатного числа дорівнює добуткові показника степеня на логарифм основи цього степеня

1.

2.

3.

4.

5.

Узагальнені формули логарифмування

1.

2.

3.

Формула переходу від однієї основи логарифма до іншої

Наслідки формули переходу від однієї основи логарифма до іншої

1.

2.

3.

Арифметична прогресія

Арифметичною прогресією називають послідовність , кожен член якої,починаючи з другого, дорівнює попередньому, до якого додається одне й те саме число d, яке називають різницею арифметичної прогресії:

.

Наприклад: 1, 2, 3, 4,…, n,… - арифметична прогресія, у якій , d=1; 2, 4, 6,…, 2n,… -

арифметична прогресія, у якій , d=2.

Визначається n-й член арифметичної прогресії за формулою

,

де n – номер члена, - n-й член, - перший член, d – різниця прогресії.

Кожний член арифметичної прогресії, починаючи з другого, дорівнює середньому арифметичному двох сусідніх членів:

.

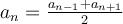Якщо всі члени деякої числової послідовності, починаючи з другого, задовольняють умові

, то ця послідовність є арифметичною прогресією.

Сума перших n членів арифметичної прогресії дорівнює середньому арифметичному першого і n-го членів цієї прогресії, помноженому на їх кількість:

.

Суму перших n членів арифметичної прогресії можна знайти і за формулою

.

Геометрична прогресія

Геометричною прогресією називають послідовність , кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на одне й те саме число q (q≠0,

|q|≠1), яке називають знаменником геометричної прогресії:

, де .

Наприклад: 1, 3, 9,…, 3n-1,… - геометрична прогресія, у якій , q=3;

- геометрична прогресія, у якій .

Визначається n-й член геометричної прогресії за формулою

,

де n – номер члена, - n-й член, - перший член, q – знаменник прогресії.

Модуль кожного члена геометричної прогресії, починаючи з другого, є середнім геометричним двох сусідніх членів:

.

Якщо всі члени числової послідовності, починаючи з другого задовольняють умові

,

то ця послідовність є геометричною прогресією.

Суму перших n членів геометричної прогресії можна знайти і за формулою

.

Нескінченно спадна геометрична прогресія

Нескінченно спадна геометрична прогресія – це нескінченна геометрична прогресія, знаменник q якої за модулем є меншим за 1, тобто |q|<1.

Сумою всіх членів нескінченної спадної геометричної прогресії

є границя, до якої прямує сума n її перших членів при нескінченному зростанні n ().

.

Ця сума визначається за формулою

Приклад. Обчисліть суму.

.

Відповідь: 2.

Розв’язування найпростіших тригонометричних рівнянь

Рівняння

Окремі випадки

Рівняння

Окремі випадки

Рівняння

Окремі випадки

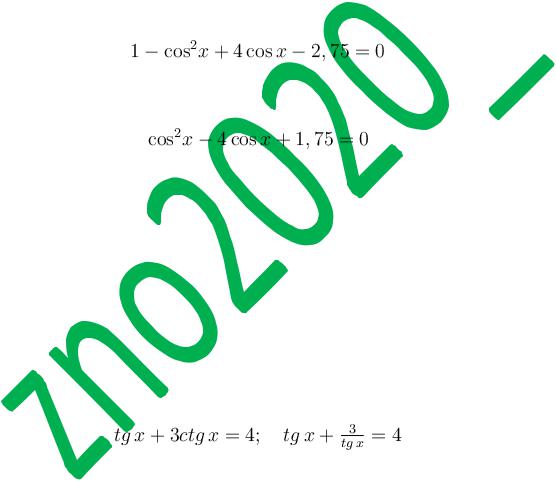
Методи розв’язування тригонометричних рівнянь

Зведення тригонометричних рівнянь до алгебрагічних

Деякі тригонометричні рівняння можна привести шляхом тотожних перетворень до рівнянь з однією тригонометричною функцією, потім зробити заміну і привести рівняння до алгебрагічного.

Розглянемо приклади.

Приклад 1. Розв’яжіть рівняння .

Розв’язування

Замінивши на , маємо:

,

;

.

Нехай cos x=t, тоді . Звідси .

Оскільки , то - розв’язків немає.

Оскільки , то .

Відповідь: .

Приклад 2. Розв’яжіть рівняння tg x+3ctg x=4.

Розв’язання

.

Нехай tg x=t, тоді .

Маємо:

1);

2).

Відповідь: .

Графіки деяких функцій та їх основні властивості

Функція

Властивості:

1.Область визначення: R.

2.Функція є непарною.

3.Для функція зростає, якщо ; спадає, якщо

.

4.Область значень: R.

5.Графік – пряма, що проходить через початок координат.

Функція

Властивості

1.Область визначення: .

2.Функція є непарною.

3.Якщо , функція спадає на проміжку і на

проміжку . Якщо , функція зростає на проміжку і на проміжку

.

4.Область значень: .

5.Графік функції – гіпербола.

Функція

Властивості

1.Область визначення: R.

2.Функція є парною.

3.Якщо , функція спадає на проміжку (-∞;0], зростає на проміжку [0;+∞). Якщо , функція зростає на проміжку (-∞;0], спадає на проміжку

[0;+∞).

4.Область значень: якщо , то ;

якщо , то .

5. Графік функції – парабола.

Функція

Властивості

1.Область визначення: R.

2.Функція є непарною.

3.Для функція зростає, якщо 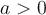; спадає, якщо

.

4.Область значень: R.

5.Графік функції – кубічна парабола.

Функція

Властивості

1.Область визначення: R.

2.Функція є парною.

3.На проміжку (-∞;0] функція спадає; на проміжку [0;+∞) функція зростає.

4.Область значень: [0;+∞).

Функція

1.Область визначення: .

2.Функція є парною.

3.Якщо , функція зростає на проміжку і спадає на проміжку . Якщо , функція спадає на проміжку і зростає на проміжку .

4.Область значень: якщо 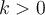, то ; якщо

, то .

Функція

Властивості

1.Область визначення: [0;+∞).

2.Функція ні парна, ні непарна.

3.На проміжку [0;+∞) функція зростає.

4. Область значень: [0;+∞).

Функція, обернена до даної

Функцію, яка набуває кожного свого значення в єдиній точці області визначення, називають

оборотною.

Наприклад: функція у=2х+1 – оборотна, а функція (визначена на всій числовій осі) не є оборотною.

Якщо функція задана формулою , то для знаходження оберненої функції потрібно розв’язати рівняння відносно х, а потім поміняти місцями х і у.

Наприклад: оберненою до функції є функція .

Якщо рівняння відносно х має більше ніж один корінь, то функція не має оберненої функції.

Наприклад: функція оберненої функції не має.

Графіки даної функції і оберненої до неї симетричні відносно прямої у=х.

Наприклад: функції , графіки яких симетричні відносно прямої у=х, є оберненими. Якщо функція

зростає (спадає) на деякому проміжку, то вона

оборотна. Функція, яка обернена до даної і визначена в області значень функції , також є зростаючою (спадною).

Якщо функція визначена на області визначення D і має область значень Е, то обернена функція має область визначення Е і область значень D.

Методи розв’язання нерівностей

Метод інтервалів

Щоб розв’язати нерівність , де , де – різні числа, треба:

1.зобразити на координатній прямій (ці числа, розташовані у порядку зростання, розділяють пряму на проміжків, на яких функція f(x) зберігає свій знак);

2.визначити знаки функції f(x) на кожному проміжку;

3.записати відповідь.

Наприклад: .