
Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
Второй
параграф будет еще интереснее, чем
первый. Задание на вычисление объема
тела вращения вокруг оси ординат – тоже
достаточно частый гость в контрольных
работах. Попутно будет рассмотрена задача
о нахождении площади фигуры вторым
способом – интегрированием по оси ![]() ,
это позволит вам не только улучшить
свои навыки, но и научит находить наиболее
выгодный путь решения. В этом есть и
практический жизненный смысл! Как с
улыбкой вспоминала мой преподаватель
по методике преподавания математики,
многие выпускники благодарили её
словами: «Нам очень помог Ваш предмет,
теперь мы эффективные менеджеры и
оптимально руководим персоналом».
Пользуясь случаем, я тоже выражаю ей
свою большую благодарность, тем более,
что использую полученные знания по
прямому назначению =).
,
это позволит вам не только улучшить
свои навыки, но и научит находить наиболее
выгодный путь решения. В этом есть и
практический жизненный смысл! Как с
улыбкой вспоминала мой преподаватель
по методике преподавания математики,
многие выпускники благодарили её
словами: «Нам очень помог Ваш предмет,
теперь мы эффективные менеджеры и
оптимально руководим персоналом».
Пользуясь случаем, я тоже выражаю ей
свою большую благодарность, тем более,
что использую полученные знания по
прямому назначению =).
Рекомендую для прочтения всем, даже полным чайникам. Более того, усвоенный материал второго параграфа окажет неоценимую помощь при вычислении двойных интегралов.
Пример 5
Дана
плоская фигура, ограниченная
линиями ![]() ,
, ![]() ,
, ![]() .
.
1)
Найти площадь плоской фигуры, ограниченной
данными линиями.
2) Найти объем тела,
полученного вращением плоской фигуры,
ограниченной данными линиями, вокруг
оси ![]() .
.
Внимание! Даже если вы хотите ознакомиться только со вторым пунктом, сначалаобязательно прочитайте первый!
Решение: Задача состоит из двух частей. Начнем с площади.
1) Выполним чертёж:
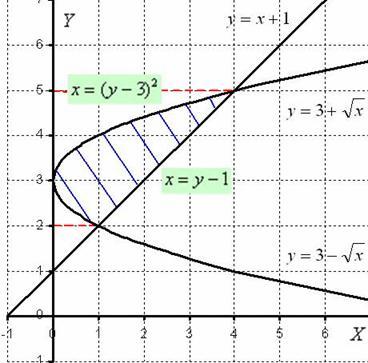
Легко
заметить, что функция ![]() задает
верхнюю ветку параболы, а функция
задает
верхнюю ветку параболы, а функция ![]() –
нижнюю ветку параболы. Перед нами
тривиальная парабола, которая «лежит
на боку».
–
нижнюю ветку параболы. Перед нами
тривиальная парабола, которая «лежит
на боку».
Нужная фигура, площадь которой предстоит найти, заштрихована синим цветом.
Как
найти площадь фигуры? Её можно найти
«обычным» способом, который рассматривался
на уроке Определенный
интеграл. Как вычислить площадь фигуры.
Причем, площадь фигуры находится как
сумма площадей:
– на отрезке ![]()
![]() ;
–
на отрезке
;
–
на отрезке ![]()
![]() .
.
Поэтому: ![]()
Чем в данном случае плох обычный путь решения? Во-первых, получилось два интеграла. Во-вторых, под интегралами корни, а корни в интегралах – не подарок, к тому же можно запутаться в подстановке пределов интегрирования. На самом деле, интегралы, конечно, не убийственные, но на практике всё бывает значительно печальнее, просто я подобрал для задачи функции «получше».
Есть
более рациональный путь решения: он
состоит в переходе к обратным функциям
и интегрированию по оси ![]() .
.
Как
перейти к обратным функциям? Грубо
говоря, нужно выразить «икс» через
«игрек». Сначала разберемся с параболой:
![]()
Этого
достаточно, но убедимся, что такую же
функцию можно вывести из нижней ветки:
![]()
Для
самопроверки рекомендую устно или на
черновике подставить координаты
2-3-х точек параболы в уравнение ![]() ,
они обязательно должны удовлетворять
данному уравнению.
,
они обязательно должны удовлетворять
данному уравнению.
С
прямой всё проще: ![]()
Теперь
смотрим на ось ![]() :
пожалуйста, периодически наклоняйте
голову вправо на 90 градусов по ходу
объяснений (это не прикол!). Нужная нам
фигура лежит на отрезке
:
пожалуйста, периодически наклоняйте
голову вправо на 90 градусов по ходу
объяснений (это не прикол!). Нужная нам
фигура лежит на отрезке ![]() ,
который обозначен красным пунктиром.
При этом на отрезке
,
который обозначен красным пунктиром.
При этом на отрезке ![]() прямая
прямая ![]() расположена
выше параболы
расположена
выше параболы ![]() ,
а значит, площадь фигуры следует найти
по уже знакомой вам формуле:
,
а значит, площадь фигуры следует найти
по уже знакомой вам формуле: ![]() .
Что поменялось в формуле? Только буква,
и не более того.
.
Что поменялось в формуле? Только буква,
и не более того.
! Примечание:
Пределы интегрирования по оси ![]() следует
расставлять строго
снизу вверх!
следует
расставлять строго
снизу вверх!
Находим площадь:
На
отрезке ![]()
![]() ,
поэтому:
,
поэтому:
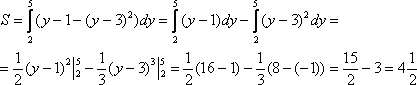
Обратите внимание, как я осуществил интегрирование, это самый рациональный способ, и в следующем пункте задания будет понятно – почему.
Для
читателей, сомневающихся в корректности
интегрирования, найду производные:

Получена исходная подынтегральная функция, значит интегрирование выполнено правильно.
Ответ: ![]()
