Рекурсивное использование функций
Функции внутри своего тела могут вызывать сами себя. Такой вызов называется рекурсией. На основе рекурсии можно строить очень интересные алгоритмы обработки данных.
Рассмотрим функцию возведения вещественного значения Dв целую положительную степеньP. Очевидная реализация этой функции основана на использовании цикла:
double Pow (double D, unsigned P)
{
double R = 1;
for (unsigned I = 0; I < P; ++ I)
R *= D;
return R;
}
А вот та же самая функция, реализованная на основе рекурсии:
double Pow (double D, unsigned P)
{
if (P)
return Pow ( D, P – 1 ) * D;
else
return 1;
}
Основанием для рекурсии в этом примере послужило следующее рекуррентное соотношение:
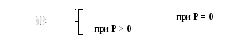
Более сложный пример рекурсии основан на следующем рекуррентном соотношении (обычная реализация этого примера приведена в разделе 5.1 конспекта):
Через рекурсию это рекуррентное соотношение реализуется так:
double T (unsigned n, double x)
{
switch (n)
{
case 0:
return 1;
case 1:
return x;
default:
return 2 * x * T (n - 1, x) - T (n - 2, x);
}
}
Как видно из этих примеров алгоритм, реализуемый через рекурсию, выглядит более компактным и понятным по сравнению с обычной реализацией. С точки зрения эффективности, реализацию этих примеров через рекурсию вряд ли можно считать более эффективной, чем обычную реализацию. Это объясняется дополнительными затратами времени на многократный вызов функций и дополнительными затратами памяти (стека) на передачу аргументов.
Однако в ряде случаев использование рекурсии позволяет достичь существенного положительного эффекта.
Рассмотрим следующий пример: необходимо написать функцию для вычисления биномиальных коэффициентов:
n>= 0, 0 <=m<=n.
Значение биномиального коэффициента определяет число различных вариантов выбора mобъектов изnобъектов (как говорят, число сочетаний изnпоm).
Основные свойства биномиальных коэффициентов:
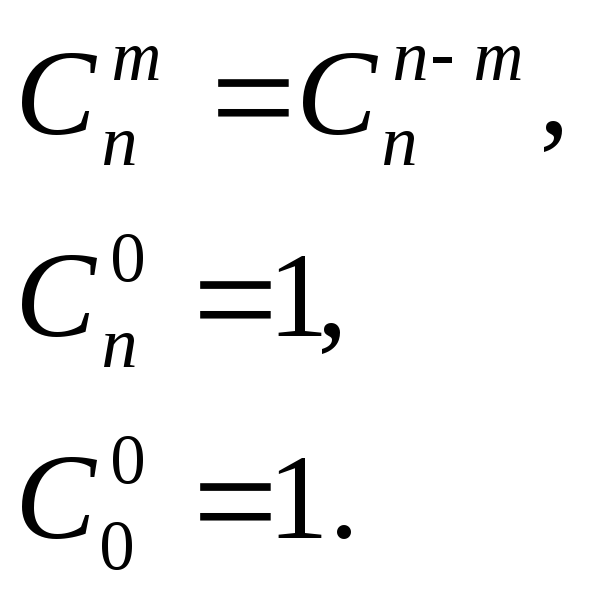
Максимальное значение биномиального коэффициента достигается при m = n / 2.
Очевидная реализация функции основана на использовании циклов для вычисления числителя и знаменателя биномиального коэффициента и нахождения частного от их деления:
unsigned C(int n, int m)
{
if (m > n / 2)
m = n - m;
unsigned a = 1, b = 1;
for (int i = n; i >= n - m + 1; -- i)
a *= i;
for (int i = 1; i <= m; ++ i)
b *= i;
return a / b;
}
Нетрудно заметить, что этот алгоритм быстро приводит к выходу значений числителя или знаменателя за пределы диапазона значений типа данных unsigned. И действительно, эксперименты с этим вариантом функции показывают, что точное вычисление биномиальных коэффициентов возможно только приn < 17.
Найдем следующее соотношение:
.
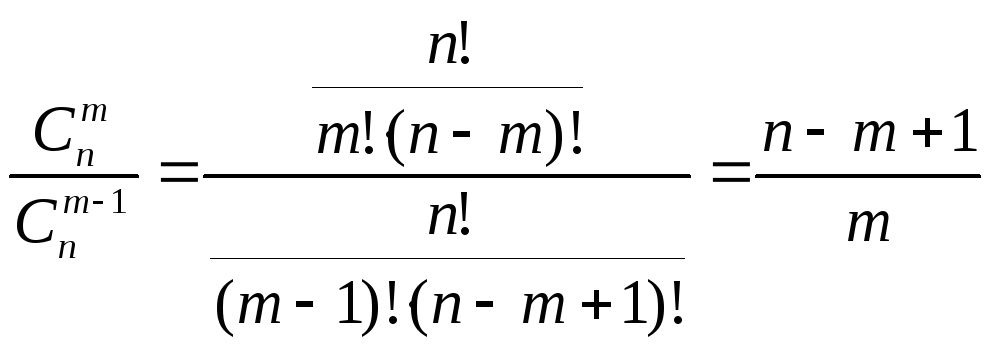То есть:
.
Тогда справедливо следующее рекуррентное соотношение, позволяющее вычислять очередное значение биномиального коэффициента через его предыдущее значение:
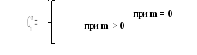
Это рекуррентное соотношение реализуется с помощью следующей рекурсивной функции:
unsigned int C(unsigned int n, unsigned int m)
{
if (m > n / 2)
m = n - m;
if (m == 0)
return 1;
else
return C(n, m - 1) * (n - m + 1) / m ;
}
Этот вариант функции позволяет точно вычислять значения биномиальных коэффициентов при n < 31. Диапазон решения расширен почти в два раза.