- •7. Преобразование Фурье (прямое, обратное, синус- и косинус-преобразование).
- •9.Двойные интегралы.Сведения двойного инт-лак повторному по прямоуг-ку и элемент обл-сти.Сведения тройного инт-ла.
- •Прилож.Крат.Интегрлов:
- •Приложения:
- •14 Потенциальные векторные поля. Потенциальность поля и эквивалентные утверждения о криволинейных интегралах второго рода.
- •След: (Выч-ие пл-ей с помощью крив-ых инт-лов)
- •19.Дивергенция.Ф-ла Остроградского и ее усл-ия
- •20.Ротор. Ф-ла Стокса. Усл-ие. Потенциальности век-ых полей в пр-ве.
- •22.Поток поля, дивергенция, соленоидальные поля.З-н сохр-ия интен-ности вект-ной трубки.
- •24.Гармонические ф-ии, сопряженные гармонические ф-ии. З-ча восстановления аналитич ф-ии по известной действит.(мнимой) части.
- •26. Первообразная функции и неопределёный интеграл. Тоерема о сущ-нии первообразной для аналитич. Ф-ии. Ф-ла Ньютона-Лейбница
- •Теорема о разложении аналит. Ф-ции в ряд Тейлора
- •Классификация с помощью рядов Лорана.
9.Двойные интегралы.Сведения двойного инт-лак повторному по прямоуг-ку и элемент обл-сти.Сведения тройного инт-ла.
Т1.
Усл-я по
прямоуг-ку :П=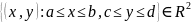 .
1) f(x,y)
инт-ма на П. 2)
.
1) f(x,y)
инт-ма на П. 2) dy=F(x)
dy=F(x)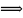 F(x)
F(x)
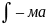 на
на
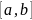 ,
т.е.
,
т.е.
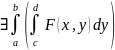 и
удов.рав-во:
и
удов.рав-во: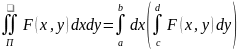
След.1: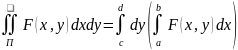 ,
F-инт-ма
и огранич на П;
,
F-инт-ма
и огранич на П;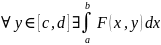
След.2:
f(x,y)
непрерывна в П ⟹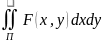 =
= =
=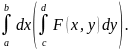 Док-во:
еслиF
непрерывна в П:
Док-во:
еслиF
непрерывна в П:
 по
Крит.
по
Крит.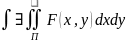
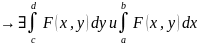
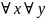
По
элемень.областиD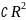
Опр.D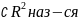 элемент-ой отн-но оси ОУ если
элемент-ой отн-но оси ОУ если
D
=(x,y):x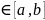 ,y
,y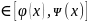 ,
где
,
где
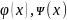 – непр-ны на
.
D
элемент-на от-но ОУ ,если
– непр-ны на
.
D
элемент-на от-но ОУ ,если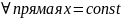 ,
x
пересекаетD
по отрезку
,
x
пересекаетD
по отрезку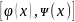 .
.
Т2.1)D элемент-на от-но ОУ. 2) Fинт-ма на Dт.е.
 .
3)
.
3)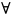 x
x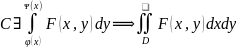 =
=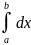 (
(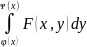 ).
Док-во:
).
Док-во:
– непр-ны на
,то
inf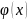 =e,
=e,
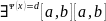
П=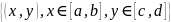
 (x,y)=
(x,y)=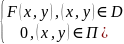
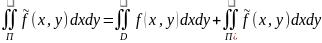 =
=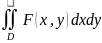
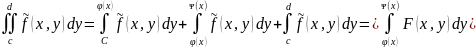
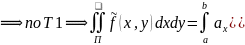
Пр.:
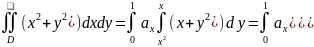 )
)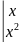 =
=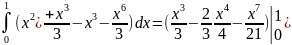 =
=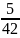
Сведения
3-го интеграла к повторному по элем.
Обл-ти. Опр.
Область
 -ой
отн-но оси Oz,если
Ω
=
-ой
отн-но оси Oz,если
Ω
=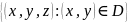 x
x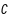 xoyz
xoyz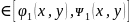 ,
D-
измерим компакт в
,
D-
измерим компакт в
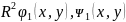 инт-ма
на
инт-ма
на
 .
.
Теорема.
1)
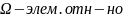 оси Oz
оси Oz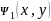
2)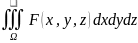
3)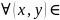 D
D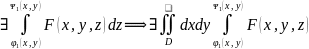
u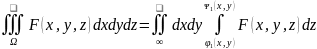
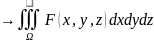 =
=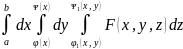
D-элем.отн-но
OY
,D
=(x,y):
x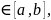 y
y
Пр.:
I=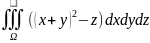 =
=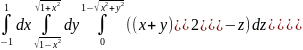
10. теоремы о замене переменных в двойном интеграле.ф-лы замены переменных при переходе поляр,цилиндр,сферичсист.коорд.
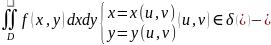 задает
отображение
задает
отображение
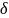 в D
в D
Пусть верны усл-я на отображ-е (*)
1)отображ-е
(*) взаимно однозначно т.е. каждой(·)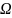 отвечает
(·)D
отвечает
(·)D
2)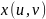 ,
,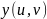 имеют в
непр-ыечастн.
Производ. 1-го порядка
имеют в
непр-ыечастн.
Производ. 1-го порядка
3)якобиан
отображения (*) J=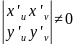 обл.
обл.
T.пусть вып-ныусл-я:
1)обл. иDквадрируемы, т.е. измеримы по Жардануобл.вR.
2)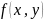 непрерыв. в
непрерыв. в
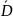 =D
=D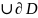
3)отображ-е
(*)обл.
в D
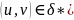 ⟹справ-ва
ф-ла зменыперемен.в 2-ом
⟹справ-ва
ф-ла зменыперемен.в 2-ом
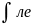
: dudv
dudv
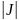 -модуль
Якобиана
-модуль
Якобиана
Замена перемен.при переходе к поляр. Сист.коорд.
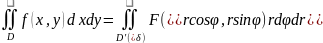
Замена перемен.в тройном
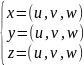 (*),
(*),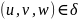
T2.
Пусть вып-ныусл-я
Т1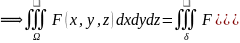 dudvdw
dudvdw
Замена перемен.при переходе к цилиндрич.сист.
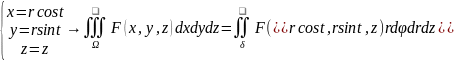
К сферич.сисит-мекоорд-т:
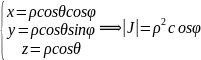
Или
: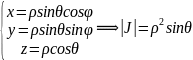
1
случ: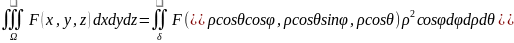
Прилож.Крат.Интегрлов:
1)площадь
фигуры: m(D)=S =
=
2)объем
ф-ры:V(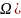 =
=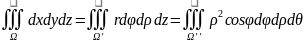
Через
2-ой интеграл: V=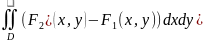 ,
,
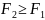 ,
,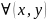
3) масса пластины/ тела:
Тела:
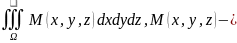 пл-ть
в(
пл-ть
в(
Пл-ны:M=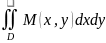
4)коорд-ты центра тяжести:
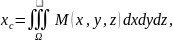 по
оси Ох,
по
оси Ох,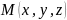 -пл-ть
-пл-ть
5)
момент инерции (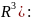 Отн-но
координат.плоскостей
Отн-но
координат.плоскостей
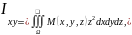
Отн-но
начала коорд-т:
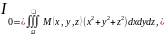
Отн-но
коорд.осей:
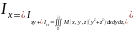
11.криволин.инт-лы 1 рода, опр.,св-ва,теорема о вычислении с помощью опред-гоинт-ла.
L-кривая
в
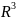 ,
L-
без самопересеч.
,
L-
без самопересеч.
L: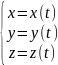 , t
, t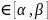
L-кусочно
ладкая: 1)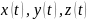 -непр-но
диф-ые
-непр-но
диф-ые
2)касат.вектор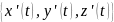 ≠0
в
≠0
в
 кривой
кривой
L-диф-ая,если
конеч.
Число ℓ(L)=supℓ(L),L-длина
кривой. Если L-
кус-но глад. Кривая без самопересеч..то
она определена и ℓ(L)= dt
dt
T-разбито

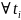 отвечают
(·)-ки
отвечают
(·)-ки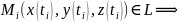 крив.
крив.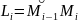 измерима
m(
измерима
m(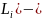 мера(длина)
мера(длина)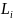
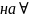 дуге
дуге
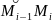 =
выберем(·)-ки
=
выберем(·)-ки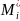
Опр.
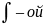 суммойназ-ся
число
суммойназ-ся
число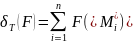 m(
m(
Опр.числоIназ-сяпределоминтегр-я
суммы
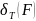 при
при
 ,
если
,
если
 разб-ияТ;такое
что
разб-ияТ;такое
что
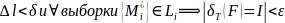 пишут
I=
пишут
I=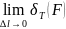
Если
число I
то Fинт-ма
по крив. LuIназ-ют
крив-ым интегралом 1 рода I= dℓ.
Св-ва:
dℓ.
Св-ва:
1)
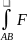 dℓ=
dℓ=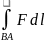
2)аддитивность:
L=L1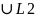 ,
L1
,
L1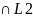 ≠0(общий
конец) и
≠0(общий
конец) и
 dℓ,
то
dℓ,
то
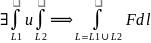 =
=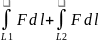
Теорема:
крив.-кусоч.глад.
без самопересеч.и ф-ция -кусоч.непрерыв.
на
-кусоч.непрерыв.
на
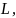 то
то
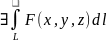 и
справ-во рав-во:
и
справ-во рав-во:
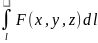 =
=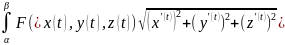 dt
dt
3)лин-ти)
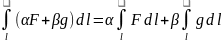
4)еслиF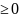 на
L,то
на
L,то
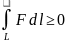
5)если
F,g-
кусоч.непрерывны и
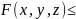 g
g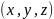 в
в
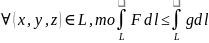
6)
если
 то
то
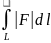 и
и
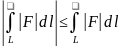
7)Fнепрерывна
на L1⟹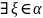 такая
что
такая
что
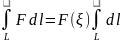 ;
L(
;
L( длина;L(
длина;L(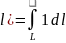
12.крив-ые интегралы 1 рода.ф-лы вычисления случ.плоск.кривой.приложения,примеры.
L
1)L-задана
пар-ческиL: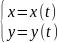 t
t
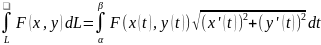
2) L-задана неявно: L:y=y(x) x

3)
L-задана
в поляр.сист.к-т:L:r=r(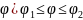
L: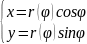
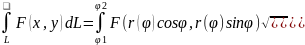
Пример:
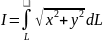 L:(
L:(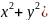 =
=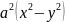
x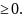 в
поляр-ую сист. Коорд-т:
в
поляр-ую сист. Коорд-т:
L(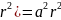 (
(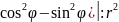
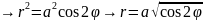 - y
- y
dL= d
d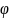


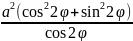 =
=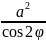
I=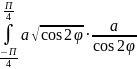 d
d