
Алмаев Р.Х. и др. Линейная алгебра в примерах и задачах Часть II
.pdf5. КВАДРАТИЧНЫЕ ФОРМЫ И ИХ ПРИМЕНЕНИЕ
Определение. Квадратичной формой n переменных x1 , x2 ,..., xn , принимающих числовые значения, называется числовая функция вида
n n
∑∑aij xi xj =a11x12 + a12 x1x2 +... + a1n x1xn + a21x2 x1 + a22 x22 +...
i=1 j =1
+a2n x2 xn +... + an1xn x1 + an2 xn x2 +... + ann xn2 ,
где aij – числа, называемые коэффициентами квадратичной формы.
Определение. Матрицей квадратичной формы n переменных x1 , x2 ,..., xn называется симметрическая матрица порядка n, элемен-
ты главной диагонали которой совпадают с коэффициентами при квадратах переменных, а каждый недиагональный элемент, расположенный в i-ой строке j-ом столбце, равен половине коэффициента при xi xj в квадратичной форме.
Определение. Рангом квадратичной формы называется ранг ее матрицы. Квадратичная форма может быть записана в матричном виде
f(xG) = xGΤ A xG, гдеA – матрицаквадратичнойформыи x = (x1, x2 ,...xn ) . Определение. Квадратичная форма называется канонической
(имеет канонический вид), если коэффициенты aij = 0 при i ≠ j , т.е.,
если матрица квадратичной формы диагональная и, следовательно,
f (xG) = a11x12 + a22 x22 +... + ann xn2 = ∑n aii xi2 ,
i=1
где не все коэффициенты aii равны нулю.
Теорема (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.
Определение. Нормальным видом квадратичной формы называется такой канонический вид, в котором коэффициенты при квадратах неизвестных (не считая нулевых) равны ±1.
Определение. Квадратичная форма f (x) называется положительно (отрицательно) определенной, если f (xG) > 0 ( f (xG) < 0) при
всех xG ≠ 0 , и положительно (отрицательно) полуопределенной, если f (xG) ≥ 0 ( f (xG) ≤ 0) при всех x .
31
ТеоремаG (критерий Сильвестра). Для того чтобы квадратичная форма f (x) была положительно определенной, необходимо и дос-
таточно, чтобы все угловые миноры матрицы квадратичной формы были положительны, т.е., чтобы
1 > 0, 2 > 0,..., n > 0.
Здесь 1, 2 ,..., n – угловыеминорыматрицыквадратичнойформы. Следствие. Для того чтобы квадратичная форма f (x) была от-
рицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров матрицы квадратичной формы чередовались сле-
дующим образом: 1 < 0, 2 > 0, 3 < 0,...,(−1)n |
n > 0. |
Примеры |
|
1. Привести квадратичную форму к каноническому виду мето-
дом Лагранжа и записать соответствующее преобразование
L(xG, xG) = x12 − x22 +3x32 + 4x1x2 + 2x2 x3 .
Решение. Следуя алгоритму метода Лагранжа, выделим вначале в квадратичной форме все члены, содержащие x1 , и дополним их до полного квадрата:
x2 |
+ 4x x = (x2 |
+ 4x x + 4x2 ) − 4x2 |
= (x + 2x )2 − 4x2 . |
||||||||||||||||||||
1 |
|
1 |
2 |
1 |
|
|
1 |
2 |
|
|
2 |
|
2 |
|
1 |
|
2 |
2 |
|
|
|||
Сделаем в этом выражении замену |
y1 = x1 + 2x2 |
и подставим его |
|||||||||||||||||||||
в квадратичную форму. В итоге получим |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
L = y2 |
−5x2 |
+3x2 |
+ 2x x . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
2 |
3 |
|
|
2 |
3 |
|
|
|
|
|
||
Далее выделим в L члены, |
содержащие x2 , и проделаем с ними |
||||||||||||||||||||||
аналогичную процедуру: |
|
|
|
|
|
|
x2 |
x2 |
|
|
|
|
|
x2 |
|||||||||
−5x2 + 2x x |
|
(x2 |
|
2 |
|
|
|
|
|
|
|
|
|
)2 + |
|||||||||
= −5 |
− |
|
|
x x |
+ |
|
3 |
− |
3 |
) = −5 (x |
|
−0.2x |
3 |
. |
|||||||||
5 |
|
25 |
25 |
|
|
||||||||||||||||||
2 |
2 |
3 |
|
|
2 |
|
|
2 |
3 |
|
|
|
|
2 |
3 |
5 |
|
||||||
Если положить |
y2 |
= x2 −0.2x3 , то квадратичная форма уже не |
|||||||||||||||||||||
будет содержать смешанных произведений. Примем также x3 = y3 , тогда канонический вид квадратичной формы есть
L = y12 −5y22 +3.2 y32 .
Соответствующее преобразование от переменных x1 , x2 , x3 к переменным y1, y2 , y3 имеет вид
y1 = x1 + 2x2 , y2 = x2 −0.2x3 , y3 = x3 .
32
2. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и записать соответствующий
канонический вид этой формы: |
|
|
|
|
|
|
L(xG, xG) = x2 + 2x2 |
+ 2x2 |
+ 2x x . |
||||
1 |
2 |
|
|
3 |
2 |
3 |
Решение. В исходном базисе |
e ,eG |
,eG |
матрица оператора, соот- |
|||
|
1 |
2 |
|
3 |
|
|
ветствующая данной квадратичной форме, есть |
|
|||||
1 |
0 |
0 |
|
|
|
|
A = 0 |
2 |
1 |
. |
|
||
0 |
1 |
2 |
|
|
|
|
Эта матрица будет определять квадратичную форму канонического вида в ортонормированном базисе e1′,eG2′,eG3′ , составленном из соб-
ственных векторов матрицы А. Найдем их. Характеристическое уравнение для матрицы А имеет вид
|
A −λ E |
|
|
|
1−λ |
|
0 |
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
0 |
2 −λ |
|
|
1 |
|
= 0 , |
||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
0 |
|
1 |
|
|
2 −λ |
|
|
|
|
|||
откуда следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(1 −λ) [(2 −λ)2 −1] = 0 |
и λ |
|
=1, λ |
3 |
=3 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
|
||
Как известно, Gсобственные векторы матрицы находятся из урав- |
|||||||||||||||||
нений ( A −λ E) f = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для случая λ1,2 =1 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
G |
|
0 |
0 |
0 |
|
α |
|
|
|
|||||
|
|
|
|
|
0 1 |
1 |
|
|
|
1 |
|
|
|
||||
|
( A − E) f |
= |
|
|
α2 = 0 . |
|
|||||||||||
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
α3 |
|
|
|||||||
Ранг матрицы этой системы уравнений (относительно α1 ,α2 ,α3 )
равен 1. Следовательно, ФСР системы состоит из двух линейно независимых решений.
Как видно из данной системы, величина α3 принимает произвольные значения, а величины α1,α2 связаны соотношением α1 +α2 = 0 . В качестве собственных можно выбратьG , например, векторы
f1 = (1,0,0), f2 = (0,1,−1).
33
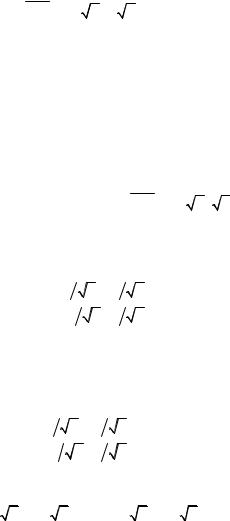
Эти векторы ортогональны: ( f1 , fG2 ) = 0 (если бы они оказались не ортогональными, то их нужно было бы ортогонализировать с
помощью стандартной процедуры). Вектор |
f1 к тому же и норми- |
|||||||
рован. Откуда следует – eG1′ = f1 . Отнормируем теперь вектор f2 : |
||||||||
eG2′ = |
|
fG2 |
|
= (0, |
1 |
, − |
1 |
) . |
|
|
|
|
|||||
|
|
f2 |
|
2 |
2 |
|
||
Для случая λ3 = 3 уравнение, |
определяющее собственный век- |
|||||||
тор, есть |
|
|
|
|
|
|
|
|
−2 |
0 |
0 |
|
β |
|
|
||
|
0 |
−1 1 |
|
|
1 |
|
= 0 . |
|
|
|
|
β2 |
|
||||
|
0 |
1 |
|
|
|
β3 |
|
|
|
−1 |
|
|
|
||||
Ранг матрицы этой системы уравнений равен 2. Следовательно,
она имеет одно линейно независимое |
|
решение, |
например, |
||||||
fG3 |
= (0,1,1). Отнормируем этот вектор: eG3′ = |
fG3 |
= (0, |
1 |
, |
1 |
) . |
||
2 |
2 |
||||||||
|
|
f |
3 |
|
|
|
|||
Теперь можно составить искомую матрицу ортогонального пре-
образования: |
|
|
|
|
|
1 |
0 |
|
0 |
|
|
|
0 1 2 1 |
2 |
|
||
Te→e′ = |
|
||||
|
0 |
−1 2 |
1 |
2 |
|
|
|
||||
Исходная квадратичная форма будет иметь следующий канониче-
ский вид: L( y, y) = y2 |
+ y2 |
+3y2 . При этом переменные x ,x , x свя- |
|||||||||||||||||||||
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
||
заны с переменными y1, y2 , y3 |
|
соотношением |
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
|
|
|
1 |
|
0 |
|
0 |
|
y |
|
|
|
|
|
|
|||||
|
|
1 |
|
= |
|
0 |
|
1 2 1 2 |
|
|
1 |
|
|
|
|
|
|||||||
|
|
x2 |
|
|
|
y2 |
|
|
|
|
|||||||||||||
|
|
x |
|
|
|
0 |
−1 2 1 2 |
|
y |
|
|
|
|
|
|
||||||||
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||
или |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
x = y |
, x = |
|
|
|
|
y |
|
+ |
y |
, x = − |
|
y |
|
+ |
y . |
|
|
||||||
|
|
2 |
|
|
2 |
|
2 |
|
2 |
|
|
||||||||||||
1 |
1 |
2 |
|
|
|
|
2 |
|
3 |
3 |
|
|
2 |
|
3 |
|
|
||||||
34
3. Построить в прямоугольной системе координат фигуру, определяемую следующим уравнением, предварительно приведя его к каноническому виду
5x2 +6xy +5y2 −16x −16 y −16 = 0 .
Решение. Выделим в этом выражении квадратичную форму L(x, y) . Это три первых слагаемых уравнения
L(x, y) = 5x2 + 6xy +5y2 .
Матрица квадратичной формы равна |
5 |
3 |
|
. Проведем про- |
|
A = |
3 |
5 |
|
||
|
|
|
|
||
цедуру приведения квадратичной формы к каноническому виду с помощью ортогонального преобразования. Характеристическое уравнение матрицы имеет вид
|
5 −λ |
3 |
|
= 0 . |
|
|
|||
|
3 |
5 −λ |
|
|
Его корни таковы: λ1 =8,λ2 = 2 .
Найдем теперь собственные векторы, соответствующие этим корням и отнормрируем их. Для вектора f1 = (α1 ,α2 ) , соответствующего λ1 =8 , имеем
G |
G |
= 0, |
−3 |
3 |
α |
|
= 0, α1 |
= α2 . |
||
( A −λ1E) f1 |
= ( A −8E) f1 |
|
3 |
−3 |
|
1 |
|
|||
|
|
|
|
|
α2 |
|
|
|
||
В итоге собственный вектор, соответствующий λ1 =8 , можно
G 1
выбрать в виде f1 = .
1
Аналогичная процедура для собственного вектора f2 = (β1 ,β2 )
G |
G |
= |
0, |
|
3 |
3 |
|
β |
|
= 0, β1 |
= −β2 , |
дает ( A −λ2 E) f2 |
= ( A − 2E) f2 |
|
3 |
3 |
|
1 |
|
||||
откуда |
|
|
|
|
|
β2 |
|
|
|
||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
−1 |
|
|
|
|
|
||
|
|
f2 |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После нормировки полученных векторов имеем
35
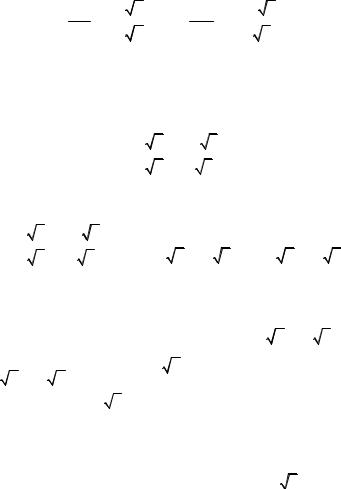
G |
|
fG1 |
|
1/ 2 |
|
G |
|
fG2 |
|
−1/ 2 |
|
||||||||||
e1′ = |
|
|
|
G |
|
|
|
= |
, |
e2′ = |
|
|
|
G |
|
|
|
= |
1/ 2 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
f |
|
|
|
1/ 2 |
|
|
|
|
|
f |
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эти векторы представляют собой ортонормированный базис новой системы координат. Матрица ортогонального оператора, при-
водящего квадратичную форму L(x, y) = 5x2 + 6xy +5y2 |
|
к канони- |
|||||||||||||||||||||||||||||||||||||||
ческому виду 8x′2 + 2 y′2 , есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ |
|
2 |
|
−1/ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T = |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1/ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
′ |
|
координат определяется со- |
|||||||||||||||||||
Связь старых (x, y) и новых (x , y ) |
|||||||||||||||||||||||||||||||||||||||||
отношением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
1/ 2 |
|
|
−1/ 2 |
|
x′ |
|
|
|
|
1 |
|
′ |
|
|
1 |
|
′ |
|
1 |
|
|
′ |
|
|
1 |
|
′ |
|
||||||||||||
= |
|
|
|
|
|
|
|
|
|
, x = |
|
x |
− |
|
|
|
|
|
|
|
x |
+ |
|
|
y |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y , y = |
|
|
|
|
|
|
||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
y′ |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
||||||
1/ 2 1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Учитывая приведенные выражения, приведем заданную квадра- |
|||||||||||||||||||||||||||||||||||||||||
тичную форму к каноническому виду |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
′2 |
|
|
|
|
|
′2 |
|
|
′ |
|
|
|
′ |
|
|
||||||
5x |
|
+ 6xy +5y |
|
−16x −16 y −16 =8x |
+ 2 y |
−16( |
|
2 x |
− |
|
|
2 |
|
− |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y ) |
||||||||||||||||||||||||||||||||
|
|
|
1 |
|
′ |
|
1 |
|
′ |
|
|
|
|
′ |
|
|
|
2 |
|
|
|
|
′2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
−16( |
2 x |
+ |
|
2 |
|
|
|
|
− |
2) |
|
+ 2 y |
−32 = 0, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
y ) −16 =8(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(x′− 2)2 |
+ |
y′2 |
=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Это есть каноническое уравнение эллипса в системе координат
′ |
′ |
, которая получается |
из исходной |
ее поворотом |
на угол |
||||||||||
x , y |
|
||||||||||||||
ϕ = π/ 4 и переносом начала координат в точку x0 |
= |
2, y0 |
= 0 . |
|
|||||||||||
Задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Записать матрицу квадратичной формы |
|
|
|
|
|
|
|
||||||||
5.1. 2x |
2 |
− x 2 |
+ 4x x ; |
5.2. x 2 |
+3x 2 |
− x x ; |
|
|
|
|
|||||
|
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
|
|
|
|
|
5.3. x 2 |
−2x 2 |
; |
|
5.4. x 2 |
−2x 2 |
+ x 2 |
−6x x ; |
|
|
||||||
|
|
1 |
|
2 |
|
|
1 |
2 |
3 |
|
1 |
3 |
|
|
|
5.5. 4x |
2 |
+ x 2 |
− 2x x ; |
5.6. 3x |
2 − x 2 |
+5x |
2 |
; |
|
|
|
|
|||
|
|
1 |
2 |
2 |
3 |
1 |
2 |
3 |
|
|
|
|
|
||
5.7. x x |
2 |
−2x x ; |
|
5.8. x 2 |
−2x 2 |
+3x |
2 |
+ 4x x |
− 2x x |
; |
|||||
|
|
1 |
1 |
3 |
|
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
||
36
5.9.3x12 +8x1x2 −3x22 + 4x32 −6x3 x4 − 4x42 ;
5.10.4x12 − 4x22 −8x2 x3 + 2x32 −4x3 x4 −5x42 ;
5.11.3x1x2 .
Найти ранг квадратичной формы
5.12.x12 + 4x22 + 4x1 x2 ;
5.13.x12 + 2x22 −6x1 x2 ;
5.14.x12 −2x22 −3x32 + 4x1 x2 + 6x1 x3 + 2x2 x3 ;
5.15.2x12 −3x22 −3x32 − 2x1 x2 + 2x1 x3 −8x2 x3 ;
5.16.2x12 − x22 +3x32 + x42 ;
5.17.2x12 +3x22 − x32 + 2x1 x2 + 2x1 x3 ;
5.18.2x12 +5x22 + 2x32 + 4x1 x2 + 4x1 x3 − 2x2 x3 ;
5.19.x12 + 2x1 x2 + x22 − 2x32 − 4x3 x4 − 2x42 ;
5.20.9x12 +5x22 +8x42 +5x32 +8x2 x3 − 4x3 x4 + 4x2 x4 .
Записать квадратичную форму в матричном виде
5.21.3x12 + 2x22 −6x1x2 ;
5.22.x22 +3x1x2 ;
5.23.2x22 − x12 ;
5.24.x12 −3x22 + x32 −4x2 x3 ;
5.25.5x12 + 2x1x3 − x2 x3 ;
5.26.x1x2 +3x1x3 −2x2 x3 ;
5.27.x12 −3x22 + x32 − 2x2 x1 −2x2 x3 ;
5.28.3x22 + x12 + 2x2 x1 −2x32 − 4x4 x3 − 2x42 ;
5.29.9x12 +5x22 +8x42 +5x32 +8x2 x3 −4x3 x4 + 4x2 x4 ;
5.30. 19x 2 |
+8x |
2 +5x 2 |
+12x x |
− 4x x |
+ 4x x . |
|
|
|
|||||
1 |
|
4 |
|
3 |
1 |
3 |
1 |
4 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
Записать квадратичную форму в виде ∑∑aij xi xj по заданной |
|||||||||||||
|
|
|
|
|
|
|
|
i=1 |
j=1 |
|
|
|
|
матрице |
|
|
|
|
|
|
|
|
|
|
|
|
|
5.31. A = |
|
1 −2 |
; |
|
|
|
|
|
0 |
1 |
; |
||
|
−2 |
|
|
|
5.32. A = |
1 |
|
||||||
|
|
3 |
|
|
|
|
|
|
|
−3 |
|
||
37
|
|
2 |
−2 0 |
|
|
|
|
3 0 2 |
|
|
|
||||||
5.33. A = |
|
−2 |
1 |
|
|
|
; |
|
5.34. A = |
|
0 |
−2 |
1 |
|
; |
|
|
|
|
−1 |
|
|
|
|
|
||||||||||
|
|
0 |
−1 0 |
|
|
|
|
|
2 1 1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
0 |
5 |
0 |
|
|
|
|
|
−1 |
3 |
0 |
|
1 |
|
||
|
|
|
|
|
|
3 |
0 |
4 |
|
0 |
|
|
|||||
5.35. A = |
|
5 |
−3 |
0 |
; |
|
|
|
5.36. A = |
|
; |
||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
4 |
2 |
|
5 |
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
0 |
5 |
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
−4 |
0 |
7 |
|
3 |
|
12 |
9 |
|
5 |
|
|
||||
|
|
0 |
2 |
5 |
|
8 |
|
|
|
|
|
||||||
5.37. А= |
|
; |
5.38. А= |
|
9 |
7 |
−2 |
; |
|
||||||||
|
|
7 |
5 |
9 |
−6 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
5 |
−2 |
|
4 |
|
|
|
||||||||
|
|
3 |
8 |
−6 |
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
6 |
3 |
|
−4 |
|
|
|
|
2 |
3 |
−7 |
|
5 |
|||
|
|
|
|
|
|
3 |
4 |
6 |
|
9 |
|
||||||
5.39. A = |
|
3 |
−4 |
|
7 |
|
; |
|
5.40. A = |
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
−7 |
6 |
3 |
|
4 |
|
|
|
|
−4 |
7 |
|
−2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
5 |
9 |
4 |
|
8 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Привести квадратичную форму к каноническому виду методом Лагранжа и записать соответствующее преобразование
5.41.x12 + 2x22 + 2x1x2 ;
5.42.x12 +5x22 + 2x32 + 2x1x2 + 2x1 x3 −2x2 x3 ;
5.43.4x12 + 2x22 +14x32 − 4x1 x2 −6x2 x3 ;
5.44.x12 −4x32 − 2x1x2 + 2x1 x3 ;
5.45.x22 + x32 + x1x3 −2x2 x3 ;
5.46.x1x2 − x1x3 ;
5.47.x12 + 2x22 + x42 + 4x1x2 + 4x1 x3 + 2x1 x4 + 2x2 x3 + 2x2 x4 ;
5.48.x1x2 + x1x3 + x1 x4 + x2 x3 + x2 x4 + x3 x4 ;
5.49.x1x2 + x2 x3 + x3 x1;
5.50.4x12 + x22 + x32 − 4x1 x2 + 4x1 x3 −3x2 x3 ;
5.51.x12 +5x22 − 4x32 + 2x1 x2 − 4x1 x3 ;
5.52.2x1 x2 + 4x1 x3 − x22 −8x32 .
38
Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и записать соответствующий канонический вид квадратичной формы
5.53. |
2x |
2 + 2x |
2 + 2x x |
; |
|
|
1 |
2 |
1 |
2 |
|
5.54. |
x 2 |
+ 2x 2 |
+ 2 6x x ; |
||
|
1 |
2 |
|
1 |
2 |
5.55.2x1x2 ;
5.56.3x12 +3x22 −2x1 x2 + 4x1 x3 + 4x2 x3 ;
5.57.7x12 +7x22 +7x32 + 2x1 x2 + 2x1 x3 + 2x2 x3 ;
5.58.2x1x2 + 2x1x3 ;
5.59.x12 + x22 + x32 − 2x1 x2 −2x1 x3 −2x2 x3 ;
5.60.6x12 +5x22 + 7x32 − 4x1x2 + 4x1 x3 ;
5.61.11x12 +5x22 + 2x32 +16x1x2 + 4x1 x3 −20x2 x3 ;
5.62.x12 + x22 +5x32 −6x1x2 −2x1 x3 + 2x2 x3 .
Записать данное уравнение второго порядка в матричном виде и определить, фигуру какого типа (эллиптического, гиперболического, параболического) оно определяет
5.63.x2 −3xy + 2 y2 −4x +5 = 0;
5.64.4x2 + 4xy + y2 − x +5y = 0;
5.65.3x2 − 2xy + y2 + 2x − y −1 = 0;
5.66.2 y2 + xy −3x + 4 y +3 = 0;
5.67.3x2 − 4xy −2 y2 +3x −12 y −7 = 0;
5.68.4x2 +5xy +3y2 − x +9 y −12 = 0;
5.69.x2 −6xy +9 y2 −12x +36 y + 20 = 0;
5.70.4x2 + 4xy + y2 −8x − 4 y − 21 = 0;
5.71.3x2 −6xy + 2 y2 − 4x + 2 y +1 = 0;
5.72.6x2 + 4xy + y2 + 4x − 2 y + 2 = 0;
5.73.2x2 +10xy +12 y2 −7x +18y −15 = 0;
5.74.3x2 −8xy +7 y2 +8x −15y + 20 = 0 .
39

Построить в прямоугольной системе координат Оху фигуру, определяемую данным уравнением, предварительно приведя его к каноническому виду
5.75. 3x2 − 2xy +3y2 −4x +12 y +10 = 0; 5.76. x2 +6xy + y2 + 4 2x +8 2 y −1 = 0;
5.77.5x2 +12xy +3 13x −36 = 0;
5.78.x2 −2xy + y2 + 4x −4 y + 4 = 0;
5.79. |
3x2 + 2 2xy + 4 y2 + 6x + 2 |
3y −1 = 0; |
5.80. |
x2 + 4xy + y2 +3 2x +3 2 y |
+ 6 = 0; |
5.81.9x2 −24xy +16 y2 −10x +55y = 0;
5.82.7x2 + 48xy −7 y2 −10x +10 y = 0;
5.83. x2 − 2xy + y2 + 2 2x + 2 y = 0;
5.84. 9x2 −24xy +16 y2 −15x + 20 y + 6 = 0 .
Каждую из квадратичных форм исследовать на знакоопределенность
5.85.x12 + 2x22 −2x1x2 ;
5.86.x12 + 2x22 −6x1x2 ;
5.87.x12 −3x22 +3x32 + 2x2 x3 − x1 x2 ;
5.88.6x12 +3x22 +5x32 + 2x1 x2 + 4x1 x3 − 2x2 x3 ;
5.89.−8x12 −5x22 −6x32 + 4x1x2 −2x1 x2 + 2x2 x3 ;
5.90.x12 −2x22 +3x32 − 4x42 + x1 x4 +6x2 x3 ;
5.91.2x12 +3x22 − x32 + 2x1x2 + 2x1 x3 ;
5.92.2x12 +5x22 + 2x32 + 4x1x2 + 4x1 x3 −2x2 x3 ;
5.93.5x12 +5x22 +5x32 +5x42 −10x1 x2 + 2x1 x3 + 6x1 x4 + 6x2 x3 ;
5.94.4x12 +3x22 + 6x32 −6x1 x2 −6x1 x3 + 2x2 x3 ;
5.95.−x12 + 2x1x2 − 4x22 ;
5.96.12x1x2 −12x1x3 + 6x2 x3 −11x12 −6x22 −6x32 .
40
