Алмаев Р.Х. и др. Линейная алгебра в примерах и задачах Часть II

в качестве минора, определяющего ранг матрицы. Тогда окаймляющие его миноры третьего порядка должны быть равны нулю. Один из них, т.е. определитель системы, уже равен нулю. Значит необходимо, чтобы выполнялось равенство

Откуда получаем

β1 −β2 −β3 = 0 .

ФСР этой системы состоит из двух линейно независимых решений

которые и составляют базис пространства образов. Таким образом,

ранг рассматриваемого оператора равен 2, а Im f ={λ1 e1′ +λ2 eG2′} .

Задачи

4.26. Найти ядро и область значений линейного оператора f: X→X, заданного в некотором базисе e1 , e2 , e3 матрицей

4.27. Найти ядро и область значений тождественного оператора. 4.28. Найти ядро и область значений линейного оператора f:

X→X, если x X f(x) = 0.

4.29. В пространстве E2 дан линейный оператор f, ортогонально

проектирующий всякий вектор а этого пространства на ось Ox. Найти ядро и область значений оператора f.

4.30.В каком случае ядро линейного оператора f линейного пространства X состоит только из нулевого вектора?

4.31.В пространстве E3 дан линейный оператор f, ортогонально

проектирующий всякий вектор а этого пространства на плоскость Oxy. Найти ядро, область значений, ранг и дефект оператора f.

11

4.32. Пусть a – фиксированный ненулевой вектор евклидова пространства E3 . Найти ядро, область значений, ранг и дефект

оператора f: E3 → E3 , если x E3 : а) f(x) = (x,a) a; б) f(x) = [x, a]. 4.33. Найти ядро, область значений, ранг и дефект линейного

оператора f: X→X, матрица которого равна A, если

4.34. Найти ядро, область значений, ранг и дефект линейного оператора f: E3 → E3 , если x E3 f(x) = kx, где k ≠ 0.

4.4. Действия с линейными операторами

Пусть f и g – линейные операторы, действующие в пространстве X. Определение. Операторы f и g считаются равными, если f(x)= g(x)

для любого x X.

Определение. Суммой двух линейных операторов f и g называется оператор h = f + g, действующий по правилу h(x) = (f + g) (x) = = f(x) + g(x) для любого x X.

Определение. Произведением линейного оператора f на число λ называется оператор h = λf, действующий по правилу h(x) = (λf) (x) = = λf(x).

Определение. Произведением линейных операторов f и g называется оператор, обозначаемый f•g или fg и определяемый равенством fg(x) = f(g(x)) для любого x X.

При сложении линейных операторов их матрицы складываются, при умножении линейного оператора на число соответствующая ему матрица тоже умножается на это число, при умножении линейных операторов соответствующие им матрицы перемножаются.

Определение. Линейный оператор называется невырожденным, если его матрица невырожденная.

Определение. Оператор g называется обратным оператору f, если fg = gf = I, где I – тождественный оператор.

12

Найти матрицу оператора

а) f + g в базисе e1′, e2′ ; б) fg в базисе e1 , e2 .

4.36. Даны линейные операторы f, g, h. Доказать, что

а) f + g = g + f; б) (f + g) + h = f + (g + h); в) f(g + h) = fg +fh; г) f(gh) = (fg)h. 4.37. Пусть в пространстве E2 даны прямые l1 иl2 , пересекаю-

щиеся под углом α, f – оператор симметрии относительно l1 , g – оператор симметрии относительно l2 . Доказать, что fg – оператор

поворота на угол 2α.

4.38. Даны линейные операторы f и g соответственно с матрицами

этом же базисе матрицу оператора а) f + g; б) fg; в) gf.

Найти матрицу оператора

а) f + g в базисе e1, e2 ; б) f + g в базисе e1′, e2′ ; в) fg в базисе e1, e2 ; г) gf в базисе e1′, e2′ .

4.40. Пусть в пространстве E2 f –оператор поворота на угол α≠0,

g– симметрия относительно оси Oy. Равны ли между собой операторы fg и gf ?

4.41. Пусть в пространствеE2 f – симметрия относительно оси Ох; g – симметрия относительно оси Oy; h – симметрия относительно биссектрисы первого и третьего координатных углов; ϕ –

13

поворот на угол α. По данному вектору а построить вектор b и найти матрицу указанного оператора в базисе i, j, если

а) b = fg(a); б) b = gf (a); в) b = fh(a); г) b = gϕ(a); д) b = ϕg(a); е) b = (ϕg) f (a).

4.42. Пусть в пространстве E3 f – симметрия относительно

плоскости Охy; h – оператор, ортогонально проектирующий всякий вектор на плоскость Oyz; g – оператор, переводящий всякий вектор x в вектор λx, где λ R. В базисе i, j, k, найти матрицу оператора

вкотором даны координаты всех векторов.

4.45.Являетсялиневырожденнымлинейныйоператорf: X→X, если а) существует ненулевой вектор x X, для которого f(x) = 0;

б) ff = I, где I – тождественный оператор; в) f(x) = 0 только в том случае, если x = 0.

4.46.Является ли невырожденным линейный оператор f: Е3→Е3,

если для фиксированного ненулевого вектора a E3 и x E3

а) f(x) = [x, a]; б) f(x) = (x, a) a.

4.47. В пространстве E2 найти оператор f −1 , обратный оператору f, если

а) f – симметрия относительно оси Ох; б) f – поворот на угол α. 4.48. Являются ли операторы f и g взаимно обратными, если из-

вестно, что fg = I, где I – тождественный оператор?

14

4.49. В некотором базисе пространства X задана матрица A линейного оператора. Выяснить, существует ли оператор, обратный данному, и если существует, найти его матрицу в том же базисе, если

4.5. Собственные векторы линейного оператора

Определение. Вектор x линейного пространства называется собственным вектором линейного оператора f этого пространства, если этот вектор ненулевой и существует число λ, такое, что f(x) =λx. При этом λ вещественное, если линейное пространство вещественное, и комплексное, если пространство комплексное. Число λ называется собственным значением оператора f.

Определение. Совокупность всех собственных значений линейного оператора называется его спектром.

Определение. Характеристическим уравнением линейного оператора называется уравнение det(A −λE) = 0 , где А – матрица это-

го оператора в некотором базисе, Е – единичная матрица того же порядка, что и матрица А.

Для того, чтобы найти собственные значения линейного оператора с матрицей А, нужно найти корни характеристического уравнения det( A −λE) = 0 . В случае комплексного пространства все

найденные корни являются собственными значениями; в случае вещественного пространства собственными значениями являются только вещественные корни.

Чтобы найти собственные векторы оператора f , находим собственные значения этого оператора. Для каждого собственного значения λ находим собственные векторы. Для этого решаем систему (А– λЕ) х= 0, где х – вектор-столбец, координаты которого являются координатами искомых собственных векторов. Любое ненулевое решение этой системы определяет собственный вектор, отвечающий собственному значению λ.

15

Примеры

1. Найти собственные значения и собственные векторы линейного оператора, заданного в некотором базисе матрицей

Решение. Найдем сначала собственные значения оператора. Ха-

(3 −λ) [(4 −λ)(2 −λ) −3] = 0.

Откуда получаем три собственных значения: λ1 =1,λ2 = 3,λ3 = 5 .

Определим теперь соответствующие собственные векторы линейного оператора. Уравнение для собственного вектора, отвечающего собственному значению λ1 , имеет следующий вид:

Откуда получаем систему уравнений для переменных α1 ,α2 ,α3 :

3α1 +α2 + 2α3 = 0, α1 +α2 = 0

Ранг матрицы данной системы равен 2, ФСР состоит из одного решения. Принимая за главные переменные α2 ,α3 , имеем:

α2 = −α1, α3 = −α1 . Таким образом, в качестве собственного вектора оператора А отвечающего собственному значению λ1 =1 , можно

1

выбрать, например, вектор xG1 = −1 .

−1

16

По аналогии для собственного вектора, отвечающего собственному значению λ2 = 3 , имеем

Откуда ясно, что переменная β3 может принимать любое значение, а для переменных β1 ,β2 получаем систему уравнений:

β1 +3β2 = 0, β1 −β2 = 0 .

Следовательно, в качестве собственного вектора оператора А, отвечающего собственному значению λ2 = 3 , можно выбрать век-

0 тор xG2 = 0 .

1

И наконец, для собственного вектора, отвечающего собственному значению λ3 = 5 , имеем

Откуда получаем систему уравнений для переменных γ1 , γ2 , γ3 :

γ1 −3γ2 = 0, 3γ1 + γ2 −2γ3 = 0 .

Принимая за главные переменные γ1 , γ2 , имеем γ1 = 53 γ3 , γ2 = γ53 .

В качестве собственного вектора оператора A , отвечающего собственному значению λ3 = 5 , можно выбрать вектор

17

3 xG3 = 1 .

5

Задачи

4.50.Дать геометрическую интерпретацию собственного вектора линейного оператора f: Е3→Е3.

4.51.Найти собственные значения и собственные векторы ли-

нейного оператора f: Е2→Е2, если

а) f – симметрия относительно оси Ох; б) f – симметрия относительно оси Оу;

в) f(x) = k x;

г) f – оператор, ортогонально проектирующий x E2 на ось Ох. 4.52. Пусть x – собственный вектор линейных операторов f и g с собственными значениями соответственно λ1 и λ2 .Доказать, что x является собственным вектором операторов fg и f + g с собственны-

ми значениями соответственно λ1 λ2 и λ1 +λ2 .

4.53. Пусть x1 , x2 – неколлинеарные собственные векторы линейного оператора f с собственными значениями соответственно λ1 и λ2 ( λ 1 ≠ λ 2 ). Является ли вектор x1 + x2 собственным вектором

оператора f.

4.54. Найти собственные значения линейного оператора вещественного линейного пространства, заданного матрицей А в некотором базисе, если

4.55.Доказать, что матрицы A и AT имеют одинаковые собственные значения.

4.56.Может ли невырожденный линейный оператор иметь собственное значение, равное нулю?

4.57.Доказать, что если λ является собственным значением

матрицы А, то λ −μ – собственное значение матрицы A −μE .

18

4.58.Доказать, что если λ ≠ 0 является собственным значением матрицы А, то 1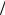λ – собственное значение матрицы A−1 .

4.59.Найти матрицу А, если известны ее собственные значения

λ1 иλ2 и собственные векторы x1 и x2 :

4.60.Доказать, что собственные векторы линейного оператора, отвечающие различным собственным значениям, линейно независимы.

4.61.Доказать, что множество собственных векторов, отвечающих одному и тому же собственному значению, вместе с нулевым вектором образуют линейное подпространство.

4.62.Найти собственные векторы линейного оператора, заданного в некотором базисе матрицей А, если

4.63. Найти собственные векторы линейного оператора f, если a) f (e1 ) = −e1 , f (e2 ) = −2e1 + 4e2 +5e3 , f (e3 ) =12e1 +3e2 +6e3 ; б) f (e1 ) = 5e1 −3e2 +12e3 , f (e2 ) = −7e1 + e2 + 6e3 , f (e3 ) = −3e3 ; в) f (e1 ) = e1 , f (e2 ) =8e1 +5e2 +3e3 , f (e3 ) = 23e1 + 7e2 + e3 .

4.64. Найти собственные значения и собственные векторы линейного оператора, заданного в некотором базисе матрицей А, если

19

4.6. Оператор простой структуры

Определение. Линейный оператор называется оператором простой структуры, если он обладает базисом из собственных векторов.

Матрица линейного оператора в базисе из собственных векторов имеет диагональную форму, в которой по главной диагонали стоят собственные значения линейного оператора.

Теорема. Для того, чтобы существовал базис из собственных векторов оператора, необходимо и достаточно, чтобы каждому собственному значению соответствовало столько линейно независимых собственных векторов, какова его кратность.

Задачи

4.65. Выяснить, приводится ли в вещественном пространстве матрица к диагональному виду (в случае приводимости записать диагональный вид матрицы с точностью до расположения диагональных элементов)

20