
4689
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Воронежская государственная лесотехническая академия»
МАТЕМАТИКА Вариационное исчисление и оптимальное управление
Методические указания к практическим занятиям для студентов специальности
190601 – Автомобили и автомобильное хозяйство
Воронеж 2011
2
УДК 517.97
Курина, Г. А. Математика. Вариационное исчисление и оптимальное управление [Текст] : методические указания к практическим занятиям для студентов специальности 190601 – Автомобили и автомобильное хозяйство / Г. А. Курина, Ю. А. Саломатова ; М-во образования и науки РФ, ФГБОУ ВПО «ВГЛТА». – Воронеж, 2011. – 27 с.
Печатается по решению учебно-методического совета ГОУ ВПО «ВГЛТА» (протокол № 7 от 24 июня 2011 г.)
Рецензент заведующий кафедрой нелинейных колебаний ВГУ д-р физ.-мат. наук, проф. В.Г. Задорожний
3
Оглавление
Введение………………………………………………………………………4
1.Вариационное исчисление………………………………………..……….5
1.1.Теоретическая часть… ……………… ……………………………6
1.2. Практическая часть……………………......................................... |
13 |
1.3.Задачи для самостоятельного решения ………………………....16
1.4.Вопросы для самоконтроля и повторения………………………17
2.Оптимальное управление…..…………….……………………………....18
2.1.Теоретическая часть…..…………….……………………………....18
2.2.Практическая часть..………………… …………..……………...20
2.3.Задачи для самостоятельного решения …………………..........26
2.4.Вопросы для самоконтроля и повторения…………………........26
Библиографический список…………….…………………......……………27
4
Введение
Наряду с задачами, в которых необходимо определить максимальные и минимальные значения (экстремумы) некоторой числовой функции y  f (x) , в инженерной практике нередко возникает необходимость найти экстремумы величин особого рода, называемых функционалами.
f (x) , в инженерной практике нередко возникает необходимость найти экстремумы величин особого рода, называемых функционалами. Функционалами называются числовые функции, значения которых определяются выбором одной или нескольких функций. То есть, при задании функционала Φ Φ( x ) число Φ соответствует функции x(t) , в то время как в случае задания функции y
Функционалами называются числовые функции, значения которых определяются выбором одной или нескольких функций. То есть, при задании функционала Φ Φ( x ) число Φ соответствует функции x(t) , в то время как в случае задания функции y  f (x) число y соответствовало числу x .
f (x) число y соответствовало числу x .
Примером функционала является длина l дуги кривой, соединяющей две заданные точки, так как эта величина определяется выбором функции, графиком которой является кривая. Как известно, величина l может быть вычислена,
если задано уравнение кривой x |
x(t), t |
t0 ,t1 |
: |
|
|
|
|
t1 |
|
|
|
l |
l(x) |
1 |
x t 2 dt. |
||
t0
Методы, позволяющие находить экстремумы интегральных функциона-
лов
t1
x
t0
F t, x t , x t
t  dt,
dt,
изучаются в разделе математики, называемом «вариационное исчисление». Задачи, в которых требуется исследовать функционал на экстремум, называются вариационными задачами.
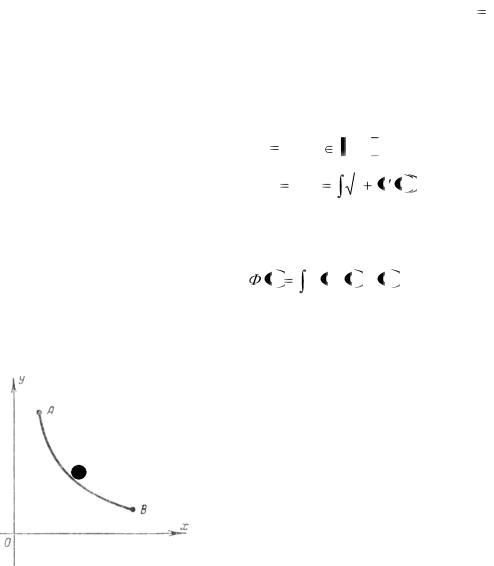
Годом рождения вариационного исчисления принято считать 1696 год, когда И. Бернулли опубликовал постановку так называемой задачи о брахистохроне (кривой наискорейшего спуска). В этой задаче требуется определить кривую, соединяющую две заданные точки А и В, не лежащие на одной вертикальной прямой, и обладающую тем свойст-
Рис. 1 |
вом, что материальная точка под действием силы |
|
тяжести скатится по этой кривой из точки А в точку В за кратчайшее время (см. рис. 1). Решение задачи о брахистохроне было дано И. Бернулли, Я. Бернулли, Г. Лейбницем, И. Ньютоном и Г. Лопиталем. Оказалось, что линией быстрейшего спуска является циклоида.
Первая часть методических указаний посвящена основным понятиям вариационного исчисления. Выводится необходимое условие экстремума функционалов – уравнение Эйлера.
5
Физические процессы, имеющие место в технике, как правило, управляемы, т.е. могут осуществляться различными способами в зависимости от воли человека. В связи с этим возникает вопрос о нахождении наилучшего в том или другом смысле или, как говорят, оптимального управления процессом. Речь может идти, например, об оптимальности в смысле быстродействия, т.е. о достижении цели процесса за кратчайшее время, о достижении этой цели с минимальной затратой энергии и т. п.
Для решения задачи оптимального управления строится математическая модель управляемого объекта или процесса, описывающая его поведение с течением времени под влиянием управляющих воздействий и собственного текущего состояния. Создание математической модели для задачи оптимального управления включает в себя:
- формулировку цели управления, выраженную через критерий качества управления;
-определение дифференциальных уравнений, описывающих возможные способы движения объекта управления;
-определение ограничений на управление.
Основным инструментом анализа задач оптимального управления в непрерывном времени является открытый в 1956 году академиком Л. С. Понтрягиным принцип максимума, носящий теперь его имя (см. Л. С. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е. Ф. Мищенко. Математическая теория оптимальных процессов, М., «Наука», Главная редакция физико-математической литературы, изд. 3–е, 1976).
Во второй части методических указаний рассматривается один класс задач оптимального управления, а именно, задачи об оптимальном быстродействии. Формулируется принцип максимума Понтрягина, приводится пример решения задачи при помощи этого принципа.
1. Вариационное исчисление
Цель: Познакомить с основными понятиями вариационного исчисления и уравнением Эйлера. Научить использовать это уравнение при определении экстремума функционала.

6
1.1. Теоретическая часть
1.1.1. Вариация и ее свойства. Методы решения вариационных задач, т.е. задач на исследование функционалов на экстремум, сходны с методами исследования на экстремум функций. Поэтому целесообразно напомнить кратко теорию экстремума функций и параллельно ввести аналогичные понятия и рассмотреть сходные теоремы для функционалов.
1. Переменная величина y называется функцией переменной величины x , что обозначается так: y y( x ), если каждому значению x из некоторой области вещественных чисел соответствует вещественное число y , т. е. имеет место соответствие: числу x соответствует число y .
2. Приращением x аргумента функции y(x) называется разность между двумя значениями этой пе-
ременной x и x0 : |
x x x0 . |
3. Функция y(x) |
называется не- |
прерывной, если малому изменению x соответствует малое изменение функции y(x) .
I. Переменная величина называется функционалом, зависящим от функ-
ции x(t) , что обозначается так: |
x , если каждой функции x(t) из |
некоторого класса функций соответствует вещественное число , т. е. имеет место соответствие: функции
x(t) соответствует число . |
|
|
|||
II. Приращением |
или |
вариацией |
x |
||
аргумента x(t) функционала |
x |
на- |
|||
зывается |
разность |
между |
двумя |
||
функциями x(t) и x0 t : |
|
|
|
||
x t |
x(t) x0 (t) . |
|
|
||
III. Функционал |
x |
называется не- |
|||
прерывным, если малому изменению функции соответствует малое изменение функционала x .
Последнее определение нуждается в уточнении и разъяснении, так как сейчас же возникает вопрос, какие изменения функции , являющейся аргументом функционала, называются малыми или, что то же самое, какие кривые x(t) и x0 (t) считаются мало отличающимися или близкими.
Определения: |
|
|
|
|
|
|
Кривые x |
x t |
и x0 |
x0 t |
близки в смысле близости нулевого порядка, ес- |
||
ли модуль разности |
x(t) |
x0 |
t |
мал для всех значений t , при которых заданы |
||
функции x t и x0 |
t , т. е., считаются близкими кривые, близкие по ординатам. |
|||||
Кривые x |
x t |
и x0 |
x0 t близки в смысле близости первого порядка, ес- |
|||
ли модули разностей x(t) |
x0 |
t |
и x (t) x0 |
t малы для всех значений t , при ко- |
||
торых заданы функции x(t) |
и x0 (t) , т. е., |
считаются близкими кривые, близкие |
||||
по ординатам и по направлениям касательных в соответствующих точках.
|
|
|
7 |
Кривые x x t и |
x0 |
x0 t близки в смысле близости k-го порядка, если |
|
модули разностей x(t) |
x0 t |
, x (t) x0 |
t ,…, x k (t) x0k t малы для всех значений |
t , при которых заданы функции x t |
и x0 t . |
||
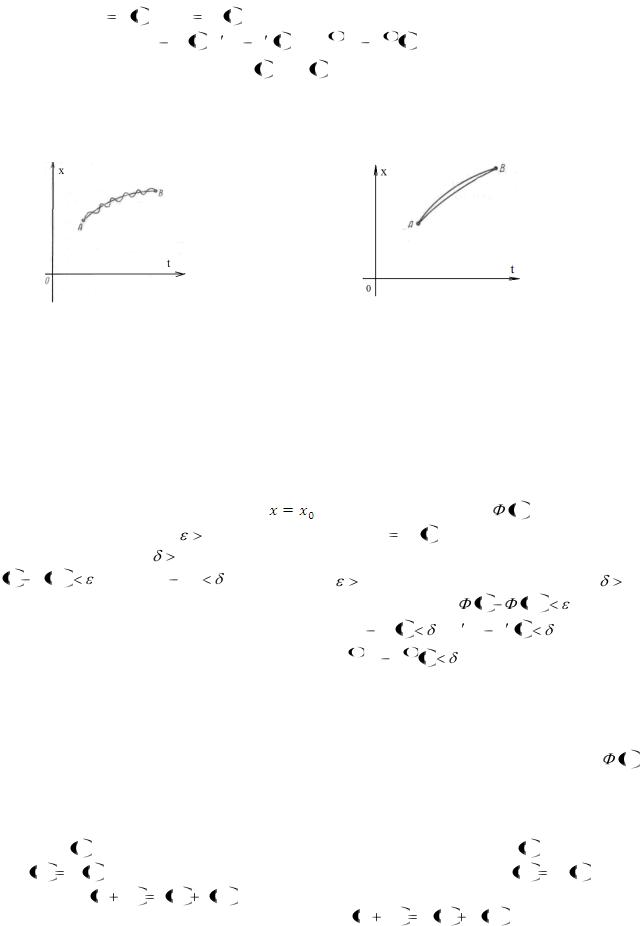
Из определений следует, что если кривые близки в смысле близости k-го порядка, то они близки в смысле близости любого меньшего порядка.
Рис. 1.1 |
Рис. 1.2 |
На рисунке 1.1 изображены кривые, близкие в смысле близости нулевого порядка, но не близкие в смысле близости первого порядка, так как ординаты у них близки, а направления касательных не близки. На рисунке 1.2 изображены
кривые, близкие в смысле близости первого порядка. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Теперь мы можем уточнить понятие непрерывности функционала. |
|
|||||||||||||||||||||
3'. Функция y(x) непрерывна при |
, |
III'. |
Функционал |
x |
непрерывен |
||||||||||||||||||
если для любого числа |
0 |
можно по- |
при x0 |
x0 |
t |
в смысле близости k - го |
|||||||||||||||||
добрать |
число |
0 |
|
такое, |
что |
порядка, |
если для |
любого |
числа |
||||||||||||||
|
y x y x0 |
, если |
x |
x0 |
|
. При этом |
0 |
|
можно подобрать число |
0 |
|||||||||||||
подразумевается, что x принимает зна- |
такое, |
что |
|
|
|
x |
x0 |
|
, |
если |
|||||||||||||
|
|
|
|
||||||||||||||||||||
чения, при которых функция y(x) |
опре- |
|
x(t) |
x0 |
t |
|
|
|
, |
|
x (t) x0 |
t |
|
|
,…, |
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||||||
делена. |
|
|
|
|
|
|
|
x k (t) |
x0k |
t |
|
|
|
|
для всех значений t , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
при которых заданы функции x(t) и |
|||||||||||||||
|
|
|
|
|
|
|
|
|
x0 (t) . При этом подразумевается, что |
||||||||||||||
|
|
|
|
|
|
|
|
функция x(t) |
берется из класса функ- |
||||||||||||||
|
|
|
|
|
|
|
|
ций, на которых функционал |
x |
||||||||||||||
|
|
|
|
|
|
|
|
определен. |
|
|
|
|
|
|
|
|
|
||||||
4.Линейной функцией называется IV. Линейным функционалом назы-
функция l x , удовлетворяющая услови- |
вается |
функционал |
L x , |
удовлетво- |
||
ям: l cx cl x , |
где |
c - произвольная по- |
ряющий условиям: |
L cx |
cL x , где |
|
стоянная, и l x1 |
x2 |
l x1 l x2 . |
c - произвольная постоянная, и |
|||
|
|
|
L x1 x2 |
L x1 L x2 . |
|
|
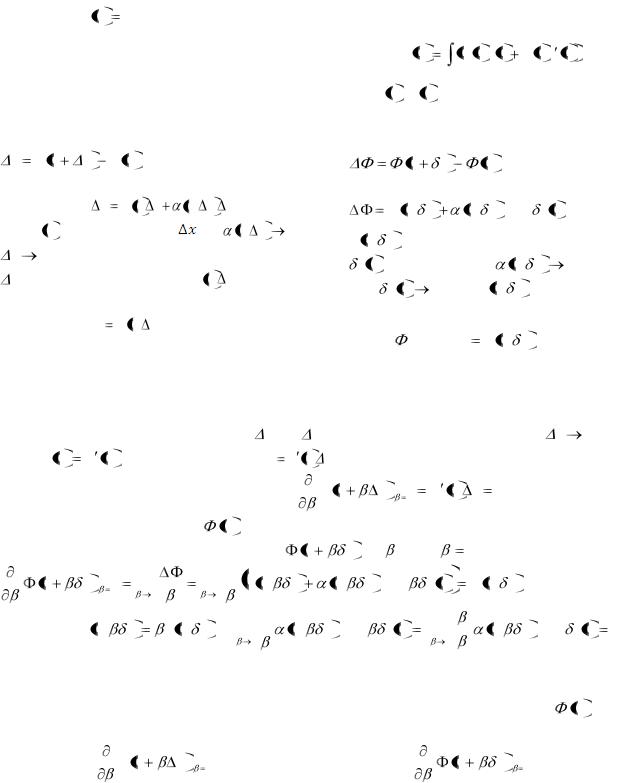
8 |
|
Линейная функция одной переменной |
Примером линейного функционала |
имеет вид l x k x, где k - постоянная. |
является |
5. |
Если |
приращение |
функции |
||||
y |
y x |
x |
y x можно |
представить |
в |
||
виде |
|
|
|
|
|
|
|
|
|
|
y A x x |
x, |
x |
x., |
|
где A x |
не зависит от |
, |
а |
x, x 0 при |
|||
x |
0, |
то |
линейная |
по |
отношению |
к |
|
x часть приращения |
A x |
x называется |
|||||
дифференциалом функции и обозначает-
ся dy , т. е., dy A x x.
x.
|
t1 |
|
|
|
L x |
p t x t q t x t dt, |
|||
|
t0 |
|
|
|
где p t , q t |
- известные функции. |
|||
V. Если приращение функционала |
||||
x |
x |
x можно предста- |
||
вить в виде |
|
|
|
|
|
|
|
, где |
|
L x, x |
x, |
x max |
x t |
|
|
|
t |
|
|
L x, x - линейный по отношению к
x t |
|
функционал, |
x, |
x 0 при |
||
max |
|
x t |
|
0 , то L x, |
x |
называется |
|
|
|||||
t |
|
|
|
|
|
|
вариацией функционала и обознача-
ется 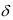 , т.е.
, т.е. 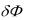 L x, x .
L x, x .
Можно дать другое, почти эквивалентное определение дифференциала функции и функционала.
|
|
Разделив выражение для |
|
y на |
x и переходя к пределу при x |
0, |
полу- |
|||||||||||||||||||||||||||||||
чим A x |
y |
x , |
следовательно, |
|
dy |
y x |
|
x. Далее, используя правило дифферен- |
||||||||||||||||||||||||||||||
цирования сложной функции, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x dy . |
|
|
|
|
|||||||||||||||||||
|
|
y x |
|
x |
|
0 |
y x |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
Пусть функционал |
x имеет вариацию в смысле главной линейной части |
|||||||||||||||||||||||||||||||||||
приращения. Найдем производную |
|
x |
|
x |
по |
при |
0 . Имеем |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x , т. к. в силу ли- |
|||||||||
|
|
x |
x |
0 |
|
lim |
|
|
|
lim |
L x, |
x |
|
x, |
x max |
|
x t |
|
|
|
|
|
L x, |
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
нейности L x, |
0 |
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
t |
|
|
lim |
|
|
|
|
x, |
|
x max |
|
x t |
|
0. |
||||||||
x |
L x, |
x , а lim |
|
x, |
|
x max |
|
x t |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Запишем новые определения: |
0 |
|
|
|
|
|
t |
|
|
|
|
|
0 |
|
|
|
|
|
|
t |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
6. Дифференциал функции y(x) ра- |
|
VI. Вариация функционала |
|
x рав- |
|||||||||||||||||||||||||||||||||
|
вен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
y x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
0 . |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Второе определение вариации несколько шире первого, так как существуют примеры функционалов, из приращения которых нельзя выделить главной линейной части, но вариация в смысле второго определения существует.

|
|
|
9 |
|
|
|
|
|
Определение. Функционал |
x |
достигает на |
кривой |
x0 (t) максимума |
||||
(минимума), если значения функционала |
x на любой близкой к x0 (t) кривой |
|||||||
x(t) не больше (не меньше), чем |
x0 т. е. |
x |
x0 |
0 |
0 . |
|||
Если |
0 ( 0 ), причем |
|
0 только при x |
x0 t |
, то говорят, что на |
|||
кривой x0 (t) достигается строгий максимум (минимум). |
|
|
|
|||||
Если функционал |
x достигает на кривой x0 (t) экстремума по отноше- |
|||||||
нию ко всем кривым, близким к x0 (t) |
в смысле близости нулевого порядка, то |
|||||||
экстремум называется сильным. |
|
|
|
|
|
|
||
Если же функционал |
x достигает на кривой x0 (t) |
экстремума лишь по |
||||||
отношению к кривым, близким к |
x0 (t) в смысле близости первого порядка, то |
|||||||
экстремум называется слабым. |
|
|
|
|
|
|
||
Очевидно, |
что если на кривой |
x0 (t) |
достигается сильный экстремум, то |
|||||
достигается и слабый, так как если кривая близка к x0 (t) в смысле близости пер-
вого порядка, то она близка и в смысле близости нулевого порядка. Однако возможно, что на кривой x0 (t) достигается слабый максимум (минимум) и не дости-
гается сильный максимум (минимум), т. е. среди кривых x(t) , близких к x0 (t) как
по ординатам, так и по направлению касательных, может не быть таких, для которых x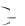 x0
x0  0 (в случае минимума x
0 (в случае минимума x x0
x0  0 ), а среди кривых x t ,
0 ), а среди кривых x t ,
близких только по ординатам, но не близких по направлению касательных, могут найтись и такие, для которых x x0
x0  0 (для минимума x
0 (для минимума x x0
x0  0 ).
0 ).
Различие между сильным и слабым экстремумом не имеет существенного значения при выводе основного необходимого условия экстремума, но оно весьма существенно при изучении достаточных условий экстремума.
7. Теорема 1.1 (необходимое условие экстремума функции). Если дифференцируемая функция y(x) достигает экстремума во внутренней точке x x0 об-
ласти определения функции, то в этой точке
dy 0.
VII. Теорема 1.1' (необходимое условие экстремума функционала). Ес-
ли функционал |
x , имеющий ва- |
риацию, достигает |
экстремума при |
x0 (t) , где x0 (t) - внутренняя точка об-
ласти определения функционала, то при x x0 t 
0.
Доказательство теоремы 1.1': При фиксированных x0 |
и |
x t рассмотрим число- |
||||||||
вую функцию от : x0 |
x |
, которая при |
0 , |
по условию, |
достигает |
|||||
экстремума. Следовательно, |
ее производная |
0 0 , |
т.е. |
|
|
x0 |
x |
|
0 0 . В |
|
|
|
|
||||||||
|
|
|||||||||
силу определения VI при x |
x0 t |
вариация |
0 . |
|
|
|
|
|
|
|
10
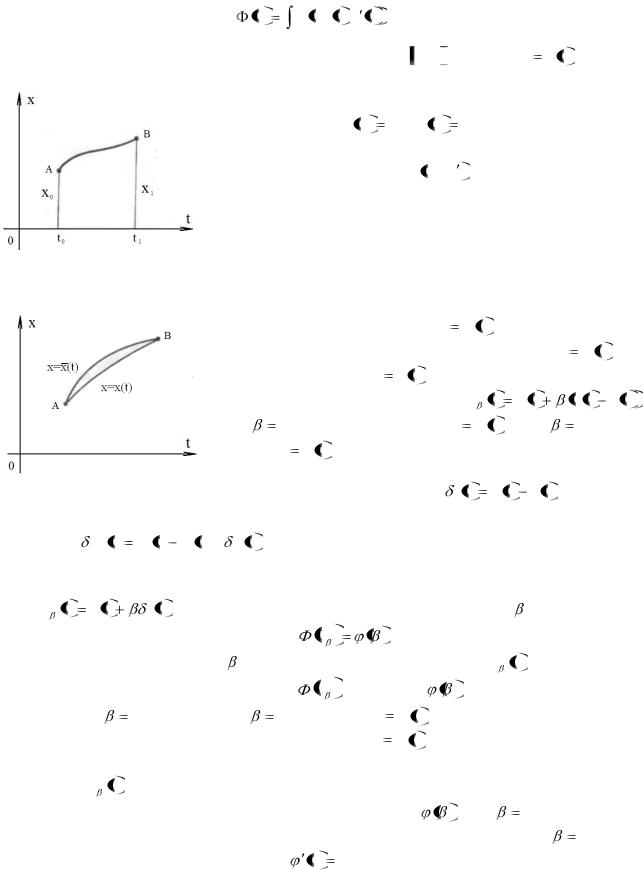
1.1.2. Уравнение Эйлера. Исследуем на экстремум функционал
|
|
t1 |
|
|
|
|
|
x |
F t, x t , x t |
dt |
|
(1.1) |
|
|
|
t0 |
|
|
|
|
на множестве непрерывно дифференцируемых на t0 , t1 функций x |
x t , удовле- |
|||||
|
творяющих условиям: |
|
|
|||
|
|
x t0 |
x0 , x t1 |
x1 , |
(1.2) |
|
|
т.е. граничные точки допустимых кривых закреплены |
|||||
|
(см. рис. 1.3). Функцию F t, x, x |
будем считать триж- |
||||
|
ды дифференцируемой. |
|
|
|||
|
В силу теоремы 1.1' необходимым условием |
|||||
|
экстремума является обращение в нуль вариации |
|||||
Рис. 1.3 |
функционала. Покажем теперь, как применяется эта |
|||||
основная теорема к рассматриваемому функционалу. |
||||||
|
||||||
|
Предположим, что экстремум достигается на дважды |
|||||
|
дифференцируемой кривой x |
x t . |
|
|||
|
Возьмем какую-нибудь близкую к |
x x t |
до- |
|||
пустимую кривую x x t |
и рассмотрим |
однопара- |
||||
метрическое семейство кривых x |
t |
x t |
x t |
x t . |
||
При |
0 получаем кривую x |
x t , |
при |
1 имеем |
||
кривую x x t (см. рис.1. 4). |
|
|
|
|
||
Рис.1. 4 |
Вариация функции |
x t |
x t |
x t |
является |
|
функцией t . Эту функцию можно дифференцировать один или несколько раз, причем,  x
x t
t  x
x 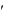 t
t  x
x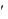 t
t  x
x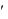 t , т. е. производная вариации равна вариации производной.
t , т. е. производная вариации равна вариации производной.
Если рассматривать значения функционала (1.1) только на кривых семей-
ства x t x t |
x t , то функционал превращается в функцию |
: |
|||
|
|
x |
, |
|
|
так как значение параметра |
определяет кривую семейства x |
t и тем самым |
|||
определяет и значение функционала x . Функция |
достигает своего экс- |
||||
тремума при |
0 , так как при |
0 получаем x |
x t |
, а функционал, по пред- |
|
положению, достигает экстремума на кривой x |
x t |
по сравнению с любой |
|||
близкой допустимой кривой и, в частности, по сравнению с близкими кривыми семейства x t .
Необходимым условием экстремума функции |
при |
0 , как извест- |
|
но из курса анализа, является обращение в нуль ее производной при |
0 : |
||
0 0 . |
|
|
|
