Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

4689

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

1.38 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 33

	Алгоритм решения задачи 2
1.	Записать матрицу A и ее транспонированную AT .
2.	Записать и решить сопряженное уравнение	dψ	AT ψ .
2.	Записать и решить сопряженное уравнение	dt	AT ψ .
		dt

3.Записать функцию ψ, Bv для найденной функции ψ .

4.Найти u(t) , доставляющее максимум по v 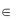функции ψ t , Bv .

5.Записать систему (2.4) для каждого из найденных значений оптимального управления. Найти соответствующие траектории.

6.Найти оптимальное управление в виде функции от фазовой точки.

Пример оформления отчета по практическому занятию

Пример 2.1. По прямой из заданного начального состояния движется по инерции точка. Требуется наискорейшим образом остановить движение этой точки в заданном месте прямой применением силы, направленной вдоль прямой и ограниченной по модулю единицей.

Решение. Сначала запишем уравнение движения точки под действием

применяемой силы – управления u u(t) :
x u .	(2.7)

Точку остановки примем за начало координат. Начальное состояние обозначим через x 0 , начальную скорость - через x 0 , время остановки – через T .

Введем новые переменные - фазовые координаты:

x ,

x . Тогда

уравнение (2.7) перепишется в виде следующей системы:

dx1

x2 ,

(2.8)

dx2

Из условия задачи следует, что x1 (0) x 0 , x 2 (0) x 0 , x1 (T )

0 ,

x 2 (T )

0 ,

1;1 ,

т.е.

u(t)

Следовательно, мы имеем линейную задачу быстродействия. Найдем решение этой задачи, используя алгоритм решения задачи 2.

1. Запишем последнюю систему в виде (2.4):

						d	x1		0	1	x1	0	u.
						dt	x 2		0	0	x 2	1	u.
Здесь x	x1	, A	0	1	, B	0	.
Здесь x	x 2	, A	0	0	, B	1	.
	x 2		0	0		1
Запишем транспонированную к A матрицу: AT													0	0 .
													1	0
2. Сопряженное уравнение								dψ		AT ψ имеет вид
2. Сопряженное уравнение								dt		AT ψ имеет вид
								dt

			d	1
			d		0,
1
1	, т. е.		dt
			dt
2		d	2
		d		1.

			dt
			dt

Найдем решение последней системы:	1	c1,	2	c1t c2 , где c1 , c	2 – произ-
	1		2

вольные постоянные.

3. Запишем функцию ψ, Bv :

	1		0
ψ, Bv	2	,	0	v	2 v.
	2		1
			1

Учитывая найденное выражение для	2 , имеем
ψ(t), Bv	c1t c2 v.
4. Найдем u(t) , доставляющее максимум по v		1;1 линейной по v функции

ψ(t), B v . Этот максимум достигается на одном из концов отрезка 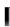1;1 в зави-

симости от знака выражения с1t	c2 . Поэтому
u(t)	sign( с1t c2 ).
Итак, каждое оптимальное управление u		u(t), t	0;T , является кусочно-
постоянной функцией, принимающей значения		1 и имеющей не более 2-х ин-
тервалов постоянства (так как линейная функция с1t			c2 не более одного раза
меняет знак на отрезке 0;T ).

5. Запишем систему (2.8) для u 1:

dx1
	x2	,

dt

dx2 1. dt

Путем интегрирования сначала второго уравнения системы, а затем – первого,

найдем решение этой системы: x1												t 2	c t	c		,	x2 t c			, где	c , c		– произволь-
найдем решение этой системы: x1													c t	c	2	,	x2 t c			, где	c , c	2	– произволь-
											2		1		2			1			1	2
											2
ные постоянные.
		Выделим в выражении для x1									полный квадрат:
x1	1	(t c )2			c 2														c 2
			c		1	.	Введя обозначение							c		c		1
			c	2		.	Введя обозначение							c		c	2
	2	1		2	2												2	2
	2				2													2
и учитывая выражение для x 2 , имеем
						x1		1	(x2 )2	c.								(2.9)
						x1	2		(x2 )2	c.								(2.9)
							2

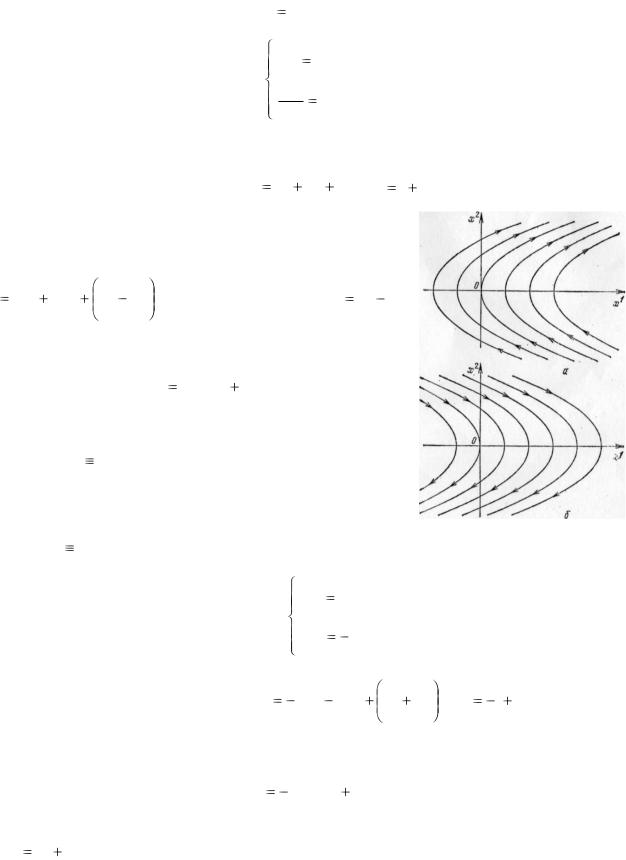
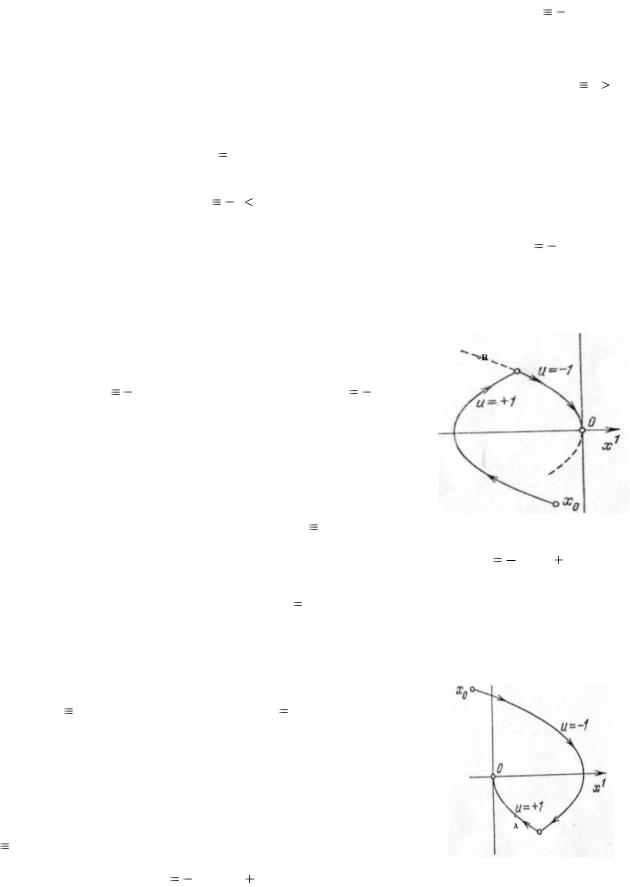
Следовательно, кусок фазовой траектории, соответствующий u 1, представляет собой дугу параболы

(2.9) (см. рис. 2.1 а).

Аналогичным образом для отрезка времени, на

Рис. 2. 1

котором u -1, имеем систему:

				dx1			x 2	,
					dt		x 2	,
					dt
				dx2			1.
					dt		1.
					dt
Решением этой системы является x1			1			(t s )2 s				s 2	, x 2 t s
										1		, где	s	, s		–
									2			, где	s	, s	2	–
			2				1		2	2	1		1		2
			2							2
произвольные постоянные. Откуда получаем
		x1	1		(x2 )2			s,					(2.10)
		x1	2		(x2 )2			s,					(2.10)
			2
	s 2
где s s2	1	.
где s s2	2	.
	2

Следовательно, кусок фазовой траектории, соответствующий u	1 ,
представляет собой дугу параболы (2.10) (см. рис. 2.1 б).
По параболам (2.9) фазовые точки движутся снизу вверх (ибо	dx2	1 0,
По параболам (2.9) фазовые точки движутся снизу вверх (ибо	dt	1 0,
	dt

то есть x 2 возрастает),	в начало координат из этого семейства парабол ведет
единственная траектория x1			1	(x2 )2 . По параболам (2.10) фазовые точки дви-
единственная траектория x1			2	(x2 )2 . По параболам (2.10) фазовые точки дви-
			2
жутся сверху вниз (ибо		dx2	1	0, то есть x 2 убывает), в начало координат по
жутся сверху вниз (ибо		dt	1	0, то есть x 2 убывает), в начало координат по
		dt
параболам из этого семейства можно попасть только по параболе x1					1	(x 2 )2 .
					2	(x 2 )2 .
					2

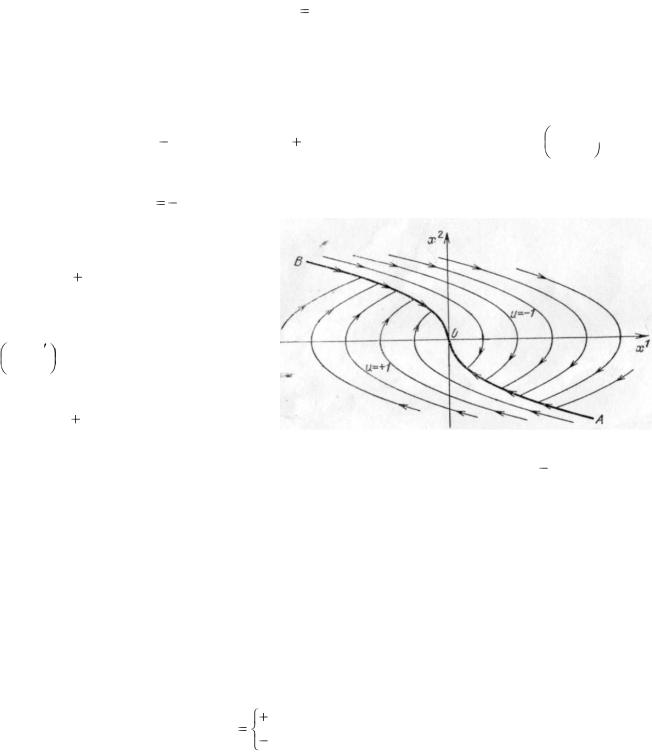
6. Построим оптимальное управление в виде функции от положения фазовой точки.

Случай 1: Пусть в точку (0,0) мы попали с

управлением u 1, то есть по параболе x1	1	(x 2 )2
	2

из второго семейства, ведущей в начало координат. Если процесс происходил без переключений, то в нуль можно попасть только по этой параболе. Если же процесс происходил с переключением, то предпоследнее значение оптимального управления u 1. При этом

управлении движение было возможно лишь по параболам

Рис. 2. 2 a

x1 12 (x 2 )2 c снизу

вверх до пересечения с параболой x1			1	(x2 )2 , расположенной в верхней полу-
вверх до пересечения с параболой x1		2		(x2 )2 , расположенной в верхней полу-
		2
плоскости (см. рис. 2.2 а).
Случай 2: Пусть в точку (0,0) мы попали с управ-
лением u 1, т. е. по траектории x1	1	(x 2 )2 из первого
лением u 1, т. е. по траектории x1	2	(x 2 )2 из первого
	2

семейства. Если процесс происходил без переключений, то в нуль можно попасть только по этой параболе. Если же процесс происходил с переключением, то предпоследнее значение оптимального управления u -1. При этом управлении движение было возможно

лишь по параболам x1	1	(x2 )2	s сверху вниз до пере-	Рис. 2. 2 б

	2

25
сечения с AO – дугой параболы x1	1	(x 2 )2	, расположенной в нижней полу-

2
плоскости (см. рис. 2.2.б).

На рисунке 2.3 изображено семейство полученных таким образом фазовых траекторий. Кривая АОВ является линией переключения. Выше этой ли-

нии управление u 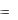1, а ниже - u 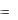1. Если начальное состояние x0 , x0 рас-

положено выше линии АОВ, то фазовая точка должна двигаться под воздейст-

вием управления u		1 до тех пор, пока она не попадет на дугу АО; в момент
попадания на дугу АО значение
u переключается и		становится
равным	1 вплоть до момента
попадания в начало координат.
Если же начальное		состояние
x0 , x0	расположено	ниже ли-
нии АОВ, то u должно быть
равным	1 до момента попада-
ния на дугу ВО, в момент попа-			Рис. 2. 3

дания на дугу ВО значение u переключается и становится равным 1 вплоть до момента попадания в начало координат (см. рис. 2.3).

Итак, согласно принципу максимума, только описанные траектории могут быть оптимальными. Из приведенного построения видно, что через каждую точку фазовой плоскости проходит одна и только одна траектория описанного вида. В теории оптимального управления доказывается, что все полученные траектории оптимальны. Других оптимальных траекторий, ведущих в начало координат, не существует.

Полученное здесь оптимальное управление можно записать следующим

образом:	u(x)	1	ниже	линии	АОВ	и	на	дуге	АО,
		1	выше	линии	АОВ	и	на	дуге	ВО.

Определение. Решение задачи, дающее оптимальное управление в виде функции от фазовой точки, называется синтезом оптимального управления.

2.3. Задачи для самостоятельного решения

Найдите оптимальное управление u(t) , которое переводит систему из состояния x 0 в начало координат за кратчайшее время при условиях:

1.	x 1	x 2 u,	1 u t 2.	6.	x 1	3u,	0 u t 1.
	x 2	u,			x 2	x 1 ,

2.	x 1		u,		u, 0 u t 1.				7.
	x 2	x 1
3.	x 1	x 2			2u,	1	u t	1.	8.
	x 2		u,

4.	x 1		u,			2	u t	1.	9.
	x 2	x 1			u,

5.	x 1	x 2	,	0	u t		2.		10.
	x 2	u,

x 1	u,		1	u t	3.
x 2	x 1	u,

x 1	x 2	u,	1	u t	1.
x 2	2u,

x 1	u,	1 u t		0.
x 2	x 1 ,

x 1	x 2	u,	1	u t	1.
x 2 2u,

2.4.Вопросы для самоконтроля и повторения

1.Сформулируйте задачу оптимального управления.

2.Сформулируйте задачу об оптимальном быстродействии.

3.Сформулируйте принцип максимума Понтрягина для задачи быстродействия.

4.Сформулируйте принцип максимума Понтрягина для линейной задачи быстродействия.

Библиографический список

Основная литература

1. Владимирский, Б. М. Математика. Общий курс [Текст] : учеб. / Б. М. Владимирский, А. Б. Горстко, Я. М. Ерусалимский. – СПб., 2008. – 960 с.

Дополнительная литература

2. Эльсгольц, Л. Э. Вариационное исчисление [Текст] / Л. Э. Эльсгольц. –

М., 1958. – 164 с.

Галина Алексеевна Курина Юлия Александровна Саломатова

МАТЕМАТИКА Вариационное исчисление и оптимальное управление

Методические указания к практическим занятиям для студентов специальности

190601 – Автомобили и автомобильное хозяйство

Редактор С.Ю. Крохотина Подписано в печать 27.12.2011. Формат 60х90 /16. Объем 1,7 п. л.

Усл. печ. л. 1,7. Уч.-изд. л. 1,9. Тираж 100 экз. Заказ ФГБОУ ВПО «Воронежская государственная лесотехническая академия»

РИО ФГБОУ ВПО «ВГЛТА». 394087, г. Воронеж, ул. Тимирязева, 8 Отпечатано в УОП ФГБОУ ВПО «ВГЛТА»

394087, г. Воронеж, ул. Докучаева, 10

7-00

<<< < Предыдущая 1 23 / 33

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.20211.37 Mб84684.pdf
#
08.01.20211.37 Mб14685.pdf
#
08.01.20211.37 Mб24686.pdf
#
08.01.20211.37 Mб14687.pdf
#
08.01.20211.38 Mб44688.pdf
#
08.01.20211.38 Mб14689.pdf
#
08.01.2021201.43 Кб0469.pdf
#
08.01.20211.38 Mб14690.pdf
#
08.01.20211.39 Mб34693.pdf
#
08.01.20211.4 Mб164695.pdf
#
08.01.20211.4 Mб24697.pdf