
2655
.pdfМинистерство образования Российской Федерации
Воронежская государственная лесотехническая академия
МОДЕЛИРОВАНИЕ ЭКОСИСТЕМ
Методические указания к выполнению лабораторных работ по разделу "Регрессионный анализ"
для студентов специальностей 260400 - Лесное хозяйство и 260500 - Лесопарковое и ландшафтное строительство
Воронеж 2002
УДК 630*5
Смольянов А.Н. Моделирование экосистем: Методические указания к выполнению лабораторных работ по разделу «Регрессионный анализ» для студентов специальностей 260400 - Лесное хозяйство и 260500 - Лесопарковое и ландшафтное строительство/ А.Н. Смольянов, А.В. Мироненко – Воронеж: ВГЛТА, 2002 - 28 с.
Печатается по решению редакционно-издательского совета ВГЛТА Научный редактор д-р с.-х. наук, проф. В.А. Бугаев Рецензент главный инженер «Воронежлеспроект» А.П. Кабанцов
3
Введение
Исследование различных лесохозяйственных взаимосвязанных признаков и процессов может быть выполнено путем моделирования.
По своей форме различают три типа моделей: графические, табличные и аналитические (математические).
Внастоящих методических указаниях рассматривается получение одномерных эмпирических моделей (с двумя переменными величинами – Х, Y). В конечном итоге полученная модель должна отражать значения зависимого, обычно известного, признака. В указанном смысле процесс моделирования можно именовать выравниванием наблюдений. Основное внимание в настоящих методических указаниях уделяется аналитическому выравниванию.
Впервой части методических указаний описано получение регрессионных уравнений с использованием ручного счета на простейшей вычислительной технике (микрокалькуляторы, логарифмическая линейка). На конкретном примере показано получение четырех регрессионных уравнений линейного (прямая) и нелинейного (парабола 2-го порядка) типа с использованием методов координат избранных точек и наименьших квадратов. Указываются различные критерии оценки адекватности уравнений.
Во второй части методических указаний рассматривается вопрос получения регрессионных уравнений на ЭВМ согласно программе STADIA. На том же примере, что и в первой части методических указаний, вычисляются 23 вида различных уравнений. Объясняется техника выбора оптимального уравнения (модели).
1 Общие положения
1.1 Выбор вида моделирования. Основы графического выравнивания
Перед началом моделирования и выбором вида модели (графический, табличный, аналитический) прежде всего необходимо установить наличие корреляционной взаимосвязи между сравниваемыми признаками. С этой целью исходные данные отображаются на графике, по которому в результате визуального осмотра делают заключение о наличии или отсутствии корреляции [1].

4
Рассмотрим особенности графического выравнивания зависимости между двумя сопряженными признаками при малой и большой выборке.
При малой выборке (N < 25…30) на графике откладываются конкретные значения отдельных наблюдений (не объединенных в классы), то есть строится так называемый точечный график. Результирующая линия проводится между точками с таким расчетом, чтобы разделить их общее количество на две приблизительно равные части. При этом необходимо стремиться к такому положению, чтобы расстояние между линией и исходными точками было кратчайшим. Для облегчения техники выравнивания и увеличения его точности можно рекомендовать следующий прием. Соединить все выравниваемые точки и постараться провести плановую выравнивающую линию по возможности ближе к этим серединам.
В результате выравнивания в нашем примере (рис.1.1), где N=16, над выравнивающей прямой расположено шесть точек, под ней семь точек и три находятся непосредственно на выравнивающей линии.
На рис.1.2 показан пример выравнивания при большой выборке, когда результаты наблюдений группируются в классы. В этом случае выравниваемые значения Y по классам Х представляют собой средние значения, полученные как среднеарифметическое из нескольких наблюдений в классе, а именно:
N
H = ∑Yi / N
i=1
где Yi – данные относительных наблюдений; H – среднеарифмитическое значение из всех наблюдений; N – число наблюдений.
Рассмотрим два способа выравнивания: без учета веса наблюдений и при учете их веса.
В случае выравнивания без учета веса наблюдений необходимо руководствоваться принципом выравнивания при малой выборке. При этом условно допускается, что все выравниваемые значения Y по классам Х имеют одинаковый “вес”, приравненный к единице.
Показанная на рисунке выравнивающая кривая (сплошная линия) разделяет исходные точки на две приблизительно равные части: четыре точки над кривой и три точки под ней. Этот способ выравнивания следует применять
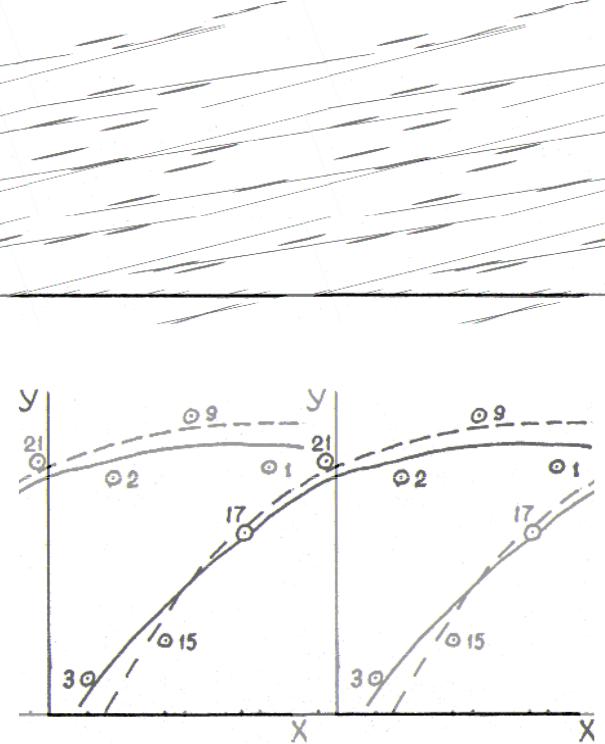
5
в тех случаях, когда во всех классах имеется равное или близкое число наблюдений.
Рис. 1.1 Графическое выравнивание взаимосвязи при малой выборке
Рис. 1.2 Графическое выравнивание взаимосвязи при большой выборке: —— без учета веса наблюдений;
- - - - с учетом веса наблюдений; о 2 число наблюдений в классе
6
Рассмотрим пример, когда в отдельных классах имеется явно различное число наблюдений, а именно:
№ классов |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
|
Число наблюдений |
3 |
15 |
17 |
21 |
2 |
9 |
1 |
|
|
|
|
|
|
|
|
Учитывая вес наблюдений, необходимо проводить выравнивающую кривую, принимая во внимание главным образом те точки, которые представлены сравнительно большим числом наблюдений. В нашем примере – классы 2, 3, 4, 6. В отличие от кривой, проведенной без учета веса наблюдений, в данном случае в начальных классах получилась более круто восходящая линия, что вызвано большим весом частот в классе 2, где n=15, и в классе 3, где n=17. Более высокое положение выравнивающей кривой в последующих классах 4 (n=21) и 6 (n=9) в сравнении с малым весом классов 5 (n=2) и 7 (n=1).
Таким образом, в результате применения любого из методов получается выравнивающая линия, которая и является графической моделью корреляционной зависимости.
Если же с полученной кривой снять значения Y по классам Х, можно получить выравненные числовые значения зависимого признака, то есть табличную модель.
Следовательно, полученные описанными способами результаты графического выравнивания могут быть использованы в двух направлениях:
1)для решения вопроса о наличии корреляционной связи, а следовательно, выяснения возможности дальнейшего аналитического (математического) моделирования;
2)как готовая графическая или табличная модель.
При выборе одного из указанных направлений необходимо учитывать, что путь графического выравнивания позволяет получить результаты сравнительно быстро, но с невысокой точностью, что объясняется невозможностью устранить субъективизм исследователя при проведении выравнивающих линий.
Аналитическое выравнивание гораздо более трудоемко, но исключает субъективность в оценках, обеспечивая получение более точных данных в виде конкретных уравнений связи двух признаков.
7
1.2 Общий подход к аналитическому выравниванию
Целью аналитического выравнивания является получение конкретного уравнения связи между двумя признаками: Х, Y. Наиболее трудным и важным вопросом в этом случае является выбор вида уравнения, намечаемого для выравнивания. С этой целью прежде всего с помощью графика решается вопрос о характере связи Х/Y: линейная или нелинейная. В случае установления линейной связи выбор модели однозначен – принимается уравнение прямой линии. Заметим, что для уверенной констатации линейной необходимо использовать данные (в случае их наличия) полного корреляционного анализа [1], [2] с получением меры линейности (Z) и ее ошибки (mz). Напомним, что имеющиеся в этом случае данные позволяют получить сразу (минуя выравнивание) конкретные уравнения корреляционной связи.
Если связь нелинейная, выбор уравнения представляет определенные трудности. В качестве модели могут быть выбраны самые различные уравнения: парабола различных порядков, гипербола, логарифмическая как показательная функция и др. При выборе необходимо значение особенностей моделируемой зависимости и математических свойств уравнений [3], [4], [5].
Допустим, что точечный график, построенный по значениям Х/Y, не позволяет сделать определенного заключения о характере связи (линейная или нелинейная). Это обуславливает необходимость производства моделирования путем вычисления регрессионных уравнений как линейной, так и нелинейной связи с последующим выбором оптимального.
В настоящих методических указаниях моделирование связи Х/Y производится с помощью уравнений различных видов. При описании техники выравнивания, выполняемого с помощью ручного счета (раздел 2), используются только два вида уравнений: прямая и парабола 2-го порядка. Получение конкретных уравнений описывается двумя способами – координат избранных точек и наименьших квадратов. При моделировании с помощью ЭВМ (раздел 3) выравнивание опытных данных производится с помощью 23 функций, полученных с использованием метода наименьших квадратов.
2Техника и способы регрессионного анализа
Вкачестве примера для аналитического выравнивания используются данные взаимосвязи двух сопряженных признаков: диаметров (Д),
8
принимаемых за Х, и высот деревьев (Н), принимаемых за Y.
Таблица 2.1 Взаимосвязь диаметров и высот (невыравненные данные)
№ классов |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Д(X), см |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
44 |
H (Y), м |
16,00 |
18,00 |
20,15 |
22,14 |
23,48 |
23,65 |
24,62 |
26,00 |
27,00 |
2.1 Выравнивание по уравнению прямой линии Аналитическое выравнивание имеет своей конечной цепью получение
конкретного уравнения связи между двумя сопряженными признаками.
Как известно, уравнение линейной зависимости общего вида будет иметь вид Y=а+b.X.
Вычисление конкретного уравнения сводится к определению числовых значений коэффициентов а, b, для получения которых существует несколько способов. Рассмотрим два, наиболее широко применяемых способа, характеризующихся различной точностью и трудоемкостью:
а) способ наименьших квадратов, позволяющий получить достаточно точные результаты путем использования координат всех выравниваемых точек (наблюдений);
б) способ координат двух избранных точек, обеспечивающий получение менее точных результатов, но гораздо более простым путем.
Остановимся на технике работ при вычислении конкретного уравнения методом координат избранных точек. В этом случае исходные данные изображаются на графике и производится предварительное выравнивание. С полученной прямой линии снимаем координаты двух любых точек исходных данных, выбирая их из числа наиболее близко расположенных по отношению к предварительно проведенной прямой. Если число наблюдений в классах известно, то следует отдать предпочтение точкам, обеспеченным наибольшим числом наблюдений. В нашем примере в качестве избранных использованы координаты точек классов № 2 и № 6.
X2=16; Y2=18,00; X6=32; Y6=23,65.
Система двух конкретных уравнений приобретет вид
Y2 =a+b.Х2
Y6 =a+b.Х6 .
После подстановки координат избранных точек
9
18,00=a+b.1623,65=a+b.32 .
После решения системы относительно a и b, получим: a=12,4; b=0,35
Следовательно, полученное конкретное уравнение связи Х/Y (Д/Н) будет иметь вид
Y= 12,4+0,35.Х . |
(1) |
Для краткости изложения в последующем тексте полученным уравнениям присвоены определенные номера: уравнение, вычисленное методом координат точек, получает номер I, а уравнение, полученное методом наименьших квадратов – номер II.
Пределы «работы» полученного уравнения по диаметру от 10 см до 46
см.
Рассмотрим технику вычислений при использовании способа наименьших квадратов. Для получения конкретного уравнения в этом случае используются координаты всех точек, которые подставляются в следующую систему уравнений
∑Y=an+b∑X ∑XY=a∑X+b∑X .
Для удобства вычислений числовых значений указанной системы составляется вспомогательная таблица.
Таблица 2.2 Вспомогательные расчеты для вычисления конкретного уравнения
прямой линии
Исходные данные |
ХY |
Х |
|
Х |
Y |
|
|
|
|
|
|
12 |
16,00 |
192,00 |
144 |
|
|
|
|
16 |
18,00 |
288,00 |
256 |
|
|
|
|
20 |
20,15 |
403,00 |
400 |
|
|
|
|
24 |
22,14 |
531,36 |
576 |
|
|
|
|
28 |
23,48 |
657,64 |
784 |
|
|
|
|
32 |
23,65 |
756,80 |
1024 |
|
|
|
|
36 |
24,62 |
886,32 |
1296 |
|
|
|
|
40 |
26,00 |
1040,00 |
1600 |
|
|
|
|
44 |
27,00 |
1188,00 |
1936 |
|
|
|
|
∑252 |
∑201,04 |
∑ 5943,12 |
∑ 8016 |
|
|
|
|
10
Подставим итоговые данные в систему уравнений и вычислим коэффициенты a, b, имея в виду, что значение «n» соответствует числу классов по Х:
201, 04 = a . 9 |
+ |
b . 252 |
|
5942 = a . 252 |
+ |
b . 8016, |
|
а=13,1; |
|
b=0,33. |
|
Следовательно, конкретное уравнение будет иметь вид |
|
||
Y=13,1+0,33.Х . |
(II) |
||
2.2 Выравнивание по уравнению параболы Используя прежний исходный материал (табл. 2.1), проделаем
выравнивание опытных данных по уравнению параболы второго порядка: Y=a+b.Х+c.Х2.
Получение конкретного уравнения указанного вида сводится, как известно, к определению числовых значений трех коэффициентов (a, b, c).
Вслучае применения способа координат избранных точек, это может быть достигнуто путем использования координат трех точек, подставленных в систему из трех уравнений. Выбор точек и составление системы уравнений выполняется аналогично вышеописываемому выравниванию по уравнению прямой линии (раздел 2.1).
Внастоящем примере воспользуемся данными (из табл. 2.1) точек № 1, 3, 8, а именно:
Х1 =12, У1 =16,0; Х 3=20, У3=20,15; Х8 =40, У8 =26,0. Составим систему из трех уравнений сначала в общем виде:
Y1 = a + b.X1 +c.X12Y3 = a + b.X3 +c.X32
Y8 = a + b.X8 +c.X82 .
азатем введем конкретное значение Х,Y:
16,0 = |
а + 12.b + 144.c |
2015 = |
a + 20.b + 400.c |
26,00 = a + 40.b +1600.c .
Врезультате решения системы получим следующее конкретное уравнение:
Y=7,8+0,77.Х - 0,008.Х2 . (II) Рассмотрим из уравнений общего вида получение конкретного
уравнения способом наименьших квадратов.
