Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2187.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

3.84 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1812 13 14 15 16 17 18 > Следующая >>>

Отсюда получаем, что	f (b) f (a)	=	f (x0)	.

(b) (a)			(x0)

§ 6. Дифференциал функции (видео 4)

Пусть функция в точке x0 имеет производную. По определению,

f (x 0) lim

, поэтому по свойствам предела

= f(x0) + (x),

x 0

где – бесконечно малая при x 0. Отсюда

y = f (x0) x + x.

Второе слагаемое

равенстве x является бесконечно малой

высшего порядка по

с x: lim

= lim (x)

= 0,

сравнению

x 0

поэтому y

f (x0) x – эквивалентные

бесконечно малые

[при

f (x0) 0].

, приращение функции y состоит из двух сла-

Таким

образом

гаемых, из которых первое f (x0) x

является главной частью при-

ращения y, линейной относительно x [при f (x0) 0].

Дифференциалом функции f (x) в точке x0							называется главная
линейная часть приращения функции и обозначается dy или d f (x0).
Следовательно,	А

		d f (x0) = f (x0) x.
Пример				Д
Найти дифференциал функции d y и приращение функции y
для функции y = x 2 при:
1) произвольных x и x;				2) при x0 = 20;		x = 0,1.
Решение.	2	2	2		2	2	2

					И
1) y = (x + x) – x = x + 2x x + ( x) – x							= 2x x + ( x) ;
			dy = 2x x;
2) если x0 = 20; x = 0,1, то				y = 40 0,1 + (0,1)2 = 4,01;

139

d y = 40 0,1= 4.

Запишем равенство y =

f (x0) x + x

в виде

y = dy + x.

Приращение y отличается от дифференциала dy на бесконечно

малую высшего порядка по сравнению с x, поэтому в приближен-

ных выч слен ях пользуются приближенным равенством

y dy;

y f (x0),

x достаточно мало.

еслиУч тывая, что y = f (x0 +

x) – f (x0), получаем формулу для

приближенных выч слений

f(x0 + x)

f(x0) + dy.

Или

f (x x0 ) f (x0 ) f

(x0 ) x.

бА

Пример

Вычислить приближенно

4,1.

Решение. Рассмотрим функцию

f (x) =

; x0 = 4; x = 0,1,

тогда

4,1 = f(x0 + x). Используя формулу приближенных вычисле-

ний,

получим

= f(x0

+ x) f(x0) + dy;

4,1

f(x0) =

4=2;

dy = f'(x0) x =

0,1 =

0,1

= 0,025.

140

Значит,

4,1 2,025.

дифференциала df (x0)

Геометрический смысл

y = f(x)

x0 x x

Проведем к графику функции y = f(x) касательную в точке M0

(x0, f (x0)), пусть – угол между касательной KM0 и осью Ox (рис. 44).

Тогда f ' (x0) = tg .

Из M0NP

ДРис. 44

	PN = tg x = f'(x0) x = d f(x0).
Но PN является приращением ординаты касательной при изме-
нении x от x0	до x0 + x. Следовательно, дифференциалИфункции f(x) в
точке x0 равен приращению ординаты касательной.
Найдем	дифференциал функции y= x. Так как (x)' = 1, то

dx = 1 x = x. Получили: дифференциал независимой переменной x равен ее приращению, то есть

141

d x = x.

Если x – произвольное число, то из равенства df (x) = f (x)

получаем

d f(x) = f (x) dx,

откуда

шению

(x) =

df (x)

или

f (x) =

Так м образом,

производная для функции y = f(x) равна отно-

бА

ее д фференц ала к дифференциалу аргумента.

Свойства дифференциала функции

Если u (x), v (x) – дифференцируемые функции, то справедливы сле-

дующиеформулы:

1. d (u + v) = du + dv.

2. d (u v) = u dv

+ v du.

3. d

= du v u dv

(v 0).

Иx

4. Инвариантность вида дифференциала.

y = f(x),

Рассмотрим дифференциал

сложной

функции

где

x = (t), то есть y = f ( (t)).

Тогда d y =

yt d t, но

так как yt

= yxxt,

поэтому d y = yxxt dt.

Учитывая, что

= d x,

получаем

d y =

d x = f

(x) d x.

Таким образом, дифференциал сложной функции

y = f (x),

где

x = (t), имеет вид dy = f (x) d x,

такой же, как в том случае, когда x

является независимой переменной. Это свойство называется инвари-

антностью формы дифференциала.

142

§ 7. Производные и дифференциалы высших порядков

Пусть функция f (x) определена и дифференцируема на некотором промежутке X, тогда ее производная f (x) также является функцией от x на этом промежутке. Если f (x) имеет производную на промежутке X, то эта производная называется производной второго порядка функции y = f (x) и обозначается y'' или f (x).

Итак, f (x) = ( f (x))'.

Вообще про зводной n-го порядка называется производная от

(n – 1)-го порядка и обозначается y(n) или f (n) (x). Итак,

(n) (x) = (f

(n-1) (x))'.

Про зводные y'', y''',

... называются производными высших по-

рядков.

производной

Пр меры

1. f (x) =

x . Найти f (x) и f (4).

Решение.

Вычисляем производные

1/2

(x) = x

;

бА

f (x) = –

x 3/2 ;

(x) =

5/2

При x = 4 получаем

(4) =

8 25 =

256.

8 45

2. Найти производную n-го порядка для функции y e3x.

Решение.

y 3e3x ;

y 3 3e3x

3 2e3x ; y''' =3 3e3x.

143

По аналогии находим y(n) = 3 ne3x.

Механический смысл второй производной

Пусть путь S, пройденный телом по прямой за время t, выражается формулой S = f(t). Известно, что при этом скорость V в момент


времени t равна производной от пути по времени: V = S (t). В момент
времени t + t скорость получит приращение
С	V			V = V(t + t) – V(t).

			называется средним ускорением за время t.
Отношен е
	t
Ускорен ем a в данный момент времени называется предел среднего
ускорен я, когда t		0:
и
a =			lim	V , т.е. a = V'(t) = (S(t))' = S''(t).
		t 0		t
Следовательно, ускорение при прямолинейном движении равно
второй производной от пути по времени:
				a = S'' (t).
бА
Перейдем к рассмотрению дифференциалов высших порядков.
Пусть y = f (x);			x X. Дифференциал этой функции y = f '(x) d x
является функцией от x; d x – приращение аргумента x не зависит от
x.
Дифференциал от дифференциалаДфункции называется диффе-
ренциалом второго порядка и обозначается d 2y или d 2f(x).
Итак,					И
				d 2y = d (dy),

но

dy= f (x)dx,

поэтому

144

d 2y = d ( f (x)dx) = ( f (x)dx)dx = f (x)(dx)2.

Будем вместо (dx)2 писать dx2.

Дифференциалом n-го порядка называется дифференциал от

дифференциала (n –1)-го порядка
С
d ny = d (d n – 1 y) = d (f (n – 1) (x)dxn – 1) = f (n)(x) dx n.
Итак,
и
Отсюда	d ny = f (n)( x) dx n.
	(n)	dn y
бА
f	(x) =	dxn .

Пр меры

1. Найти d 3y для функции y = cos2x.

Решение. d 3y = y''' dx 3. Вычислим y''', находя последовательно y', y'', y''':

y' = (cos2x)' = –2cosxsinx = –sin2x; y'' = (–sin2Дx)' = –2cos2x;

y''' = 4sin2x.

Следовательно, d 3y = 4sin2x dx 3. И

2. Вычислить с помощью дифференциала приближённое значение выражения 531.

Решение. Используем приближённое равенство

f (x) df (x) f (x) x,

верное при малых значениях x . Откуда

145

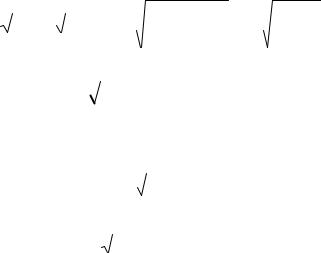
f (x0 x) f (x0 ) f (x0 ) x.

Преобразуем сначала исходное выражение

		5					5							5				32(1				1			)		25					1					1			.
				31							32 1											1															1
				31							32 1
																					32													32
						f (x) 5								;		x0					x							1				. Производная равна
	Полож м											x						1;										1
	Полож м											x						1;
Сf (x)																											32
																1				;	f (1)						1.

															55			x4
	б																А																									15
	б																А
Окончательно меем												5 31 2(1 1 (															1			))					31			1							.
Окончательно меем												5 31 2(1 1 (															32			))								1							.
и																											32							16 16
3. Найти вторую производную функции y																																							x				.
3. Найти вторую производную функции y																																											.
																																				x2 1
Решение. Сначала находим первую производную:
		y									x						x2 1 2x2														1 x2										.

										2							(x		2	1)			2						(x			2	1)						2
							x				1						(x			1)									(x				1)
Теперь вычисляем вторую производную:
	1 x2												2x(x2 1)2 4x(1 x2)(x2																															1)
	1 x2												2x(x2 1)2 4x(1 x2)(x2																															1)
	y																											И
		(x			2	1)			2															2							4
		(x				1)											Д(x 1)
	2x(x2	1) 4x(1 x2)															2x3				2x 4x 4x3																							2x3				2x		.

	(x		2			1)		3													(x			2		1)					3													(x		2	1)		3
			2					3																2							3															2			3

4. Для параметрически заданной функции																																		x a(t sint);
4. Для параметрически заданной функции																																																		най-
																																		y a(1 cost)

тивторую производную y .

Решение. Вычислим первую производную данной функции.

146

Имеем

yt = a sin t;

= a (1 – cost);

asint

sint

a(1 cost)

(1 cost)

Итак, про зводная первого порядка имеет вид

a(t sint);

sin t

(7)

1 cos t

бА

Теперь выч сляем производную от функции, заданной форму-

лой (7).

= a (1 – cost);

sint

cos x

1 cos x sin x sin x

y =

(1 cost)

1 cos x

cos x cos2 x sin2

cos x

1 cos x 2

cos x 1

Итак, вторая производная от параметрически заданной функции

это параметрически заданная функция вида

x a(t sint);

cos t 1

Задачи для самостоятельного решения

1. Вычислить с помощью дифференциала приближённые значения выражений:

147

a) sin 46о;

б) 5

;

в) 4

;

г) cos 89о.

2. Найти вторую производную функций:

;

б)

y 3sin

;

x2 1

в)

cos(xy) 1 y2;

г)

xcos2(x y) xln y;

2 arccos 3t;

3t3

4ее 7;

Сд) y y esin t;

е) y

3t 12.

y t

§ 8.

Пр менен

е дифференциального

исчисления

киисследован ю функций

I. Необход

мое

достаточное

условия

возрастания

функции

Функция f (x)

называется монотонно возрастающей на проме-

жутке X, если x1 x2

: x1 ,x2 X выполнено условие f (x1) f (x2 ).

Функция f (x) называется монотонно убывающей на X, если

: x ,x X

выполнено условие

f (x ) f (x

1бА2 1

Теорема (необходимое условие монотонности функции)

а) Если дифференцируемая функция f (x) монотонно возрастает

на

промежутке

производная

(x) существует на

X , то

f (x) 0; x X .

б) Если дифференцируемая функция

f (x) монотонно убывает

на

промежутке

производная

f (x) существует на

X , то

f (x) 0; x X .

Доказательство

а) Выберем две точки x и x x из промежутка X . Будем счи-

тать, что x 0. Тогда x x x и, поскольку, по условию, функция

f (x) монотонно возрастает на промежутке X , то

f x x f x .

148

Значит,

приращение

функции

положительно:

y f x x f x 0.

f x x f

Рассмотрим

теперь отношение

которое положительно, как отношение двух положительных функций.

Предел положительной функции не может быть отрицательным, по-

этому

lim

f x x f x

x 0 0 x

x 0 0

Поскольку

про зводная

равна

пределу отношения

вида и

(x) lim

предел не зависит от способа стремления xк ну-

x 0

лю, то

бА

(x) lim

x x

lim

x 0 x

x 0

x 0 0 x

lim

x 0 0 x

Итак, если функция монотонно возрастает на некотором проме-

жутке

и дифференцируема в

каждой

точке этого

промежутка, то

(x) 0 на этом промежутке.

Утверждение б) доказывается аналогично.

Теорема (достаточное условие монотонности функции)

а) Если

– дифференцируемая на

f (x)

функция и

(x) 0;

x X , то f (x)

монотонно возрастает на X .

f (x) 0;

б) Если f (x)

– дифференцируемая на

функция и

x X , то f (x)

монотонно убывает на X .

Доказательство

а) Пусть f

(x) 0

во всех точках промежутка

X . Возьмем две

произвольные точки x1

и x2

из X . Считаем,

что

x1 x2,

то есть

x2 x1

0. Запишем для отрезка x1 ; x2 формулу Лагранжа

x2 x1

f x2 f x1 f c

149

где с x1 ; x2 X . Так				как	с X , то	f			по	условию,
где с x1 ; x2 X . Так				как	с X , то	f		c 0,	по	условию,
x2 x1 0	–	по	выбору	точек, поэтому			f	x2 f	x1 0, или
f x2 f	x1	при условии		x2	x1, что, по определению,					означает
возрастание функции на X .
Утверждение б) доказывается аналогично.
С			Геометрический смысл
			Геометрический смысл
и
					Рис. 45
Касательная к графику монотонно возрастающей функции обра-
					Д
зует с положительным направлением оси абсцисс острый угол или
параллельнабАей (см. рис. 45).
Касательная к графику монотонно убывающей функции образу-
ет с положительным направлением оси абсцисс тупой угол или па-
раллельна ей (см. рис. 45).					И
Пример					И
Пример
Определить			промежутки		возрастания	и		убывания		функции

y 2 x2 x.

Решение. Функция определена при любых значениях переменной x. Для нахождения промежутков возрастания и убывания функции найдем ее производную:

y 4x 1.

Находим, при каких x производная положительна и отрицательна:

150

y 4x 1 0 при x 1 ; 4

y 4x 1 0 при x 1 . 4

С	1
Итак, функция возрастает на интервале	4	;	, функция
	4

		1
убывает на нтервале ;			.
убывает на нтервале ;		4	.
		4
если
II. Локальный экстремум
Пусть функц я f (x) определена на промежутке X и c X .
Говорят, что в точке c	функция f (x) имеет локальный максимум,

существует такая окрестность точки c, что для любой точки x из этой окрестности выполняется неравенство f (x) < f (c) (рис. 46, а).

Точка c называется точкой локального минимума, если существует такая окрестность точки c, что для любого значения x из этой окрестности верно условие f (x) > f(c) (рис. 46, б).

Точки локального максимума и минимума называются точками

экстремума.	Д
Замечание. Точки экстремума всегда являются внутренними
точками промежуткабА, то есть не могут совпадать с его концами.
	И
f c f x	f c f x
а	б
	Рис. 46

151

Точки локальных максимумов и локальных минимумов имеют общее название экстремумы.

Теорема (необходимое условие экстремума). Если дифферен-

цируемая в точке x c функция	y f (x) имеет экстремум в этой
точке, то f (c) 0.

Доказательство. По условию, функция y f (x) имеет в точке x c экстремум. По определению экстремума, это значит, что у точки

с существует окрестность, для всех точек которой

f c является наи-

больш м

ли на меньшим. Применим теорему Ферма к этой окрест-

ности.

По услов ю,

так как производная в точке с существует, то

f (c) 0.

Замечан я

1. Обратное

неверно. То есть производная функции

в некоторой точке может равняться нулю, но эта точка может не быть

точкой экстремума.

утверждение

Пр мер

Функц я y x3

экстремумов не имеет, однако ее производная

y 3 x2

равна нулю при x 0.

2. Функция может иметь экстремум и

в точке, в которой произ-

водная не определена или равна

есконечности.

Пример

Функция y

имеет локальный минимум при x 0. При этом

в точке x

бА

ействительно,

производная функции не определена.

0 x

y 0 lim

x 0

Точка x c называется критической точкой 1-го рода при вы-

полнении одного из условий:

(c)

или f

(c)

не существует.

Теорема (достаточное условие экстремума). Пусть функция y f (x) непрерывна, дифференцируема во всех точках некоторого интервала, содержащего точку x c, за исключением, возможно, самой точки c. Если при переходе аргумента через критическую точку с

152

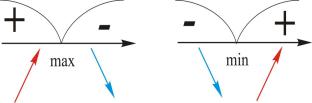
первая производная меняет знак, то данная критическая точка 1-го рода является точкой экстремума.

Если f (c) при переходе аргумента слева направо через крити-

ческую точку 1-го рода x c меняет знак с плюса на минус, то функ-
ция в этой точке имеет локальный максимум, а при перемене знака с
С		локальный минимум (рис. 47).
минуса на плюс –
Знак	f (c)
и
Поведен е
функц	y f (x)
бА
			Рис. 47
Доказательство теоремы использует признак монотонности.
Пр мер
Исследовать		на монотонность и экстремумы функцию

f (x) x2e x .

Решение. Данная функция определена и непрерывна на всей чи-

словой оси.

Найдем производную:

f (x) 2xe

(2 x).

Тогда

f (x) 0 при x1 = 0 и x2 = 2. То есть x1 , x2– критические

точки 1-го рода. Эти точки разбивают всю числовую ось на три ин-

тервала: (– ; 0), (0; 2), (2; + ). Составим табл. 1, в первой строке

которой поместим указанные точки и интервалы, во второй строчке –

сведения о знаках и нулях производной

f (x) в критических точках

и на интервалах, а в третьей – информацию о возрастании, убывании,

экстремумах данной функции f (x).

Таблица 1

( , 0)

x1 = 0

(0, 2)

x2 = 0

(2, )

f (x)

f (x) < 0

f (x) > 0

f (x) < 0

ymin (0) 0

f (x)

Убывает

Возрастает

ymax(2)

Убывает

153

Делаем выводы о поведении функции f (x):

на интервалах (– ; 0), (2; + ) функция f (x) убывает;

на интервале (0; 2) – возрастает;

x1 = 0 является точкой минимума, причем ymin(0) 0;

С						4
	x2	= 2 – точка максимума и			ymax(2)		0,54.
						e2
Теорема (достаточный признак существования экстремума,
основанный на второй производной). Пусть x c – критическая
симума					f (c) 0. Тогда
точка для функц				y f (x), причем
а) если		f	(c) 0, то x c – точка локального минимума;
б) если		f (c) 0, то x c – точка локального максимума.
Доказательство. По условию,					f (c) 0. Пусть для определен-
ности	бА
	f (c) 0. Покажем, что x c является точкой локального мак-

По определен ю второй производной, имеем равенство

f (c) lim	f c x f c		lim	f c x		.
	x
x 0			x 0		x
Так как f (c) 0, то предел lim		f	c x		0, поэтому су-

	Д
	x 0		x

ществует некоторая окрестность точки x c, во всех точках которой

верно неравенство f c x 0.

Из этого неравенства получаем, что если x 0, то f (c x) 0, что означает, что слева от точки с функция y f (x) имеет положительную производную, то есть функция возрастает.

Если x 0, то f (c x) 0, что означает, что справа от точ-

ки с функция y f (x) имеет отрицательную производную, то есть
функция убывает.	И
Получили, что при переходе через точку c слева направо знак
первой производной меняется с + на – . По признаку существования
экстремума это означает, что в точке	x c функция y f (x) имеет
локальный максимум.

154

Примеры (видео 5)

1.Найти точки экстремумов функции y 4 x2 x 4.

Решение. Функция не определена при x = 1. Найдем критические точки 1-го рода:

			4 x2 x 4							8x 1 x 1 1							4 x2 x 4
			4 x2 x 4							8x 1 x 1 1							4 x2 x 4
	y
	y															2
						x 1										2
						x 1										x 1
и																			4
				2
С4 x 8 x 5								.
				x 1 2				.
	Первая про зводная равна нулю при x2 2x																		5	0, то есть при
	Первая про зводная равна нулю при x2 2x																			0, то есть при
										x		5	;	x		1.
										x			;	x		1.
									1		2				2	2
	Найдем теперь вторую производную:
													Д
					4 x2		8 x 5				8x 8 x 1 2						4x2	8x 5			2 x 1
	y				бА
	y						2											4
						x 1											x 1
		18				.
		x 1 3				.
	Определим знаки второй производной в критических точках:
5				18										5
							0,	поэтому x								является точкой локального ми-

y			5		3									2
2			5		3									2			И
					1
			2

нимума.

155

	1				18					1
								0, поэтому x			является точкой локального

y	2				1	3				2
	2				1	3				2
						1
						1
					2
максимума.
С									x3	2x2 3x 1 на экстремум с
	2.		Исследовать функцию y							2x2 3x 1 на экстремум с
								3
помощью второй про зводной.
	Решен е. Найдём первую производную данной функции
условие
y x2		4x			3		реш м уравнение y x2 4x 3 0. Корни этого
уравнен			я x1 1; x2					3 – критические точки 1-го рода, в которых мо-
гут быть экстремумы функции, так как в них выполнено необходимое
			экстремума.
				бА
	Найдём вторую производную данной функции y 2x 4. Про-

верим, выполнены ли достаточные условия экстремума, то есть определим знак второй про зводной в критических точках: y (1) 2 0;

y (3) 2 0. Это позволяет сделать вывод, что				x1 1 – точка мак-
симума;	x2 3 – точка минимума. Вычислим значения функции в
точках экстремума:
	ymax y 1 21;	ymin y 3 1.
	Д
	2
III.	Выпуклость и вогнутость графика функции. Точки пе-
региба
График дифференцируемой функции			f (x) называется выпук-
лым (выпуклым вверх) на Х, если он расположен ниже любой своей
касательной на Х(рис. 48).			f (x) называется вогну-
График дифференцируемой функции
тым (выпуклым вниз) на Х, если он расположен выше любой своей
касательной на Х (см. рис. 48).			И

На интервалах выпуклости и вогнутости касательные, проведенные к графику, не пересекают график функции.

156

фик	Рис. 48
С

Точка x с называется точкой перегиба, если в этой точке граменяет направлен е выпуклости.

Касательная, проведенная к графику функции в точке перегиба, пересекает граф к функции в точке касания. На рис. 48 это точка А.

Теорема. Пусть функция		y f (x) определена на некотором
промежутке Х, производная	f	(x) определена во всех внутренних
точках Х. б
Тогда функция y f (x)	выпукла вверх (вниз) на Х, если и толь-

ко если производная f (x) у ывает (возрастает) во всех внутренних

точках Х.
Следствие (правилоАопределения направления выпуклости
графика функции).
	Если f (x) 0 во всех внутренних точках Х, то функция
y f (x)	выпукла вверх на Х;	И
	Если f (x) 0 во всехДвнутренних точках Х, то функция
y f (x)	выпукла вниз на Х (рис. 49).

Знак f (c)

Выпуклость функции y f (x)

Рис. 49

157

Теорема (необходимое условие точек перегиба). Пусть график

функции y f (x) имеет перегиб в точке с. Если функция y f (x)

имеет непрерывную вторую производную, то f (c) 0.

Доказательство. По условию,

функция y f (x) в точке с ме-

няет направление выпуклости, то есть слева и справа от точки пере-

(x) имеет разные знаки. По условию,

гиба с вторая производная

вторая производная

f (x) непрерывна, поэтому, по теореме Коши о

промежуточных

значениях

непрерывной

функции, получаем, что

перегиФункц я y x

ов не имеет, но при этом вторая произ-

Замечан я

что в некоторой точке с выполняется условие

1. Возможно,

f (c) 0. При этом точка с не о язательно является точкой перегиба.

Пр мер

водная равна нулю при x 0:

12 x2

при x 0.

y x4

4 x3

2. Функция y f (x) может иметь перегиб и в точке, в которой

вторая производная не определена.

ПримербА

Функция y 3

определена на всей числовой оси. Вторая про-

изводная y

не определена при x 0,

Дx

но при этом вторая производная слева и справа от x 0 принимает

разные знаки, то есть имеет разные направления выпуклости. Получа-

ем, что точка x	0 является точкой перегиба.
Точка x с	называется критической точкой 2-го рода, если
имеет место одно из условий:
f (c)	0; f (c) или	f (c) не существует.
Точки перегиба следует искать		среди критических точек 2-го
рода.

158

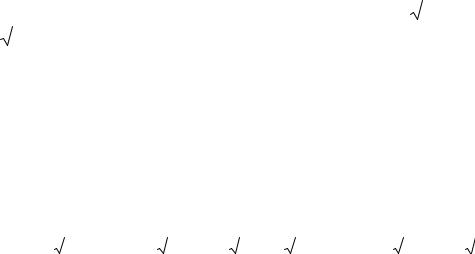
Теорема (достаточное условие существования точки переги-

ба). Пусть функция y f (x) непрерывна, дважды дифференцируема во всех точках некоторого интервала, содержащего точку x c, за ис-

ключением, возможно, самой точки c. Пусть x c – критическая точ-

ка 2-го рода. Если при переходе аргумента через точку с вторая про-

изводная функции меняет знак, то данная критическая точка 2-го рода

является точкой перегиба.

Пр мер

числим

Определ ть

нтервалы выпуклости, вогнутости и точки переги-

ба граф ка функц

y = x2 e –x.

Решен е.

Функц я определена при всех действительных x. Вы-

вторую про зводную функции f (x) = x 2 e –x:

бА

f ' (x) = 2 x e –x – x 2 e –x;

f '' (x) = 2e–x – 2xe–x – 2xe–x + x2e–x = e–x (2 – 4x + x2).

Найдем значения x, при которых f (x) = 0 и интервалы знако-

постоянства второй производной

f (c) :

f (x) = 0, e–x (2 – 4x + x2)= 0.

Найдем

корни этого

2 0,58 и

уравнения:

x1= 2 –

x2 = 2 +

3,41.

Значения функции f (x) в точках x1, x2:

y1 = f (x1) 0,34

и y2 = f (x2) 0,38.

Результаты исследования внесем в табл. 2.

Таблица 2

( , 2

x1 2

x2 2

2, )

f (x)

f (x) > 0

f (x ) =0

f (x) < 0

f (x

) =0

f (x) > 0

f (x)

Кривая

M1(x1, y1) –

Кривая

M2(x2, y2) –

Кривая

вогнутая

точка

выпуклая

точка

вогнутая

перегиба

159

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1812 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20213.77 Mб62182.pdf
#
07.01.20213.79 Mб02183.pdf
#
07.01.20213.8 Mб182184.pdf
#
07.01.20213.8 Mб2952185.pdf
#
07.01.20213.82 Mб172186.pdf
#
07.01.20213.84 Mб72187.pdf
#
07.01.20213.85 Mб12188.pdf
#
07.01.20213.85 Mб162189.pdf
#
07.01.2021356.57 Кб0219.pdf
#
07.01.20213.86 Mб112190.pdf
#
07.01.20213.86 Mб152191.pdf