Линейные отображения

Подобно теориям других алгебраических структур, линейная алгебра изучает отображения между векторными пространствами, которые сохраняют структуру векторного пространства. Линейное отображение (линейное преобразование, линейный оператор) произвольных векторных пространств над одним полем  — отображение, сохраняющее линейность:

,

.

Когда между двумя векторными пространствами существует взаимно-однозначное отображение, являющееся линейным, то эти пространства называютсяизоморфными; многие свойства векторных пространств сохраняются при изоморфных преобразованиях (инвариантны относительно изоморфизма).

Над классом всех линейных отображений данных векторных пространств можно определить структуру векторного пространства. Линейные отображения конечномерных векторных пространств могут быть записаны в матричной форме и их свойства уже изучаются средствами матриц^[⇨].

Собственные векторы и собственные числа

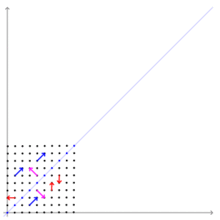
Синие и сиреневые векторы, сохраняющие направление при линейном преобразовании — собственные, красные — нет

В общем случае действие линейных отображений может быть довольно сложным. Важной и распространённой задачей является нахождение такого базиса векторного пространства , в котором матрица данного линейного отображения  имеет наиболее простой вид. При решении этой задачи ключевую роль играют инвариантные подпространствалинейного отображения  — подпространства, образ которых при отображении  вложен в себя. Если найдены инвариантные подпространства ненулевой размерности  (то есть, выполнено ), прямая суммакоторых составляет всё пространство , то матрица отображения  имеет блочно-диагональный вид с блоками порядков , на главной диагонали, если выбрать базис состоящим из  групп векторов, где -ая группа является базисом в подпространстве .

Простейшим случаем инвариантного подпространства является одномерное инвариантное подпространство , которое можно задать с помощью одного (любого) ненулевого вектора . В этом случае условие вложенности образа подпространства в себя принимает вид  с некоторым числом ; такая конструкция приводит к определению собственного вектора и собственного числа: если для некоторого вектора  и числа  выполнено равенство , то  называется собственным числом отображения , а вектор  называется его собственным вектором. Собственные числа линейного отображения определены однозначно, а собственные векторы — с точностью до пропорциональности, то есть до умножения на произвольное ненулевое число.

В случае, если отображение имеет набор  линейно независимых собственных векторов, число которых  равно размерности пространства , из них можно составить базис (называемый собственным базисом данного отображения), в котором матрица отображения диагональна, при этом на главной диагонали стоят собственные числа. Такие линейные отображения называются диагонализируемыми. Достаточным (но не необходимым) условием диагонализируемости является наличие  различных собственных чисел.

Применение

Решение систем линейных алгебраических уравнений

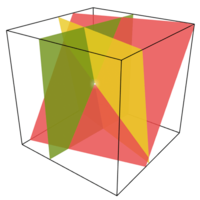
Система линейных уравнений от трёх переменных определяет набор плоскостей. Точка пересечения является решением.

Система m линейных алгебраических уравнений с n неизвестными — это система уравнений вида

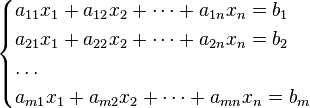
Она может быть представлена в матричной форме как:

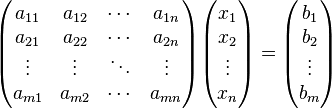
или:

.