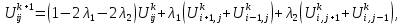Неявная схема для волнового уравнения.
Иногда удобнее использовать неявные схемы. Это схемы обычно абсолютно устойчивы, то есть не имеют ограничений на величину шага. Однако алгоритм сложнее.
|
|
|
Отсюда можно
получить:
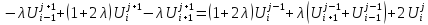 ,
где
,
где
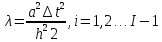 .
.
Эту систему можно
решать методом прогонки. Разностная
схема устойчива и сходится со скоростью
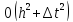 .
К этой системе нужно добавить разностные
начальные и граничные условия.
.
К этой системе нужно добавить разностные
начальные и граничные условия.
Отметим, что здесь как и выше две частных производных второго порядка, поэтому четыре краевых условия, которые записаны выше.
При наличии двух или трех независимых пространственных переменных волновые уравнения соответственно имеют вид:
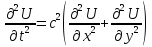

Теперь можно аппроксимировать производные по трем переменным, что усложняет алгоритм и требует больше памяти. Двумерный случай рассмотрим на примере уравнения теплопроводности.
Уравнение
теплопроводности.
Запишем его для случая двух пространственных
переменных. Положим

 .
В отличие от волнового уравнения,
требующего два начальных условия, в
уравнение теплопроводности входит
только первая производная по
.
В отличие от волнового уравнения,
требующего два начальных условия, в
уравнение теплопроводности входит
только первая производная по
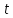 ,
поэтому необходимо задавать одно
начальное условие:
,
поэтому необходимо задавать одно
начальное условие:
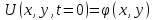 .
.
Теперь сформулируем
граничные условия. Пусть переменные
меняются в следующих пределах:
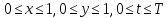 .
То есть область изменения параллелепипед.
.
То есть область изменения параллелепипед.
|
|
|
Граничные условия задаются на больших ребрах, а начальные условия на нижней грани. |
Введем трехмерную
сетку по осям
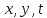 :
:
 .
Значения сеточной функции в узлах
трехмерной сетки
.
Значения сеточной функции в узлах
трехмерной сетки
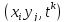 обозначим символом
обозначим символом
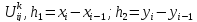 .
.
Построим явную разностную схему по следующему шаблону:
|
|
Отсюда
можно найти явное выражение для
естественной функции на слое
|
Условие устойчивости
имеет вид:

При
 ;
получается особенно простой вид схемы:
;
получается особенно простой вид схемы:
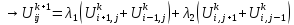 .
.
Полученная схема
сходится со скоростью
 .
.
То есть мы имеем
рекуррентные соотношения, с помощью
которых последовательно вычисляются
значения сеточной функции во внутренних
узлах слоев в
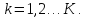 На нулевом слое используются выше
написанное начальное условие, которое
записывается в виде:
На нулевом слое используются выше
написанное начальное условие, которое
записывается в виде:
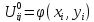 .
Здесь нельзя как __________
.
Здесь нельзя как __________
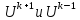 так как нет начального условия производной.
так как нет начального условия производной.
Значения
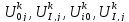 в граничных узлах вычисляется с помощью
граничных условий:
в граничных узлах вычисляется с помощью
граничных условий:
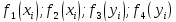 .
.
Неявную абсолютно устойчивую схему для данной задачи можно построить следующим образом:

Это уравнение можно записать в виде системы линейных алгебраических уравнений относительно значений сеточной функции на каждом слое:


Граничные условия
задаются значениями сеточной функции
в граничных узлах (то есть при
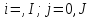 ).
Начальное условие задает значениями
сеточной функции на нулевом _______.
).
Начальное условие задает значениями
сеточной функции на нулевом _______.
Алгоритм решения,
конечно, более сложный, но существуют
______зная абсолютно устойчивые неявные
схемы, позволяющие провести расчеты со
сравнительно большим шагом по времени .
.
(то есть здесь
всё-таки
 ,
а первая неявная схема абсолютно
устойчива)
,
а первая неявная схема абсолютно
устойчива)
Основой построения
таких схем является разбиение расчета
на одном шаге по времени (то есть при
переходе от
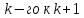 )
на отдельные этапы. Такие схемы называются
схемами
расщепления
или схемами дробных
шагов.
)
на отдельные этапы. Такие схемы называются
схемами
расщепления
или схемами дробных
шагов.
Они объединяют
преимущества явных схем (простой
вычислительный алгоритм) и преимущество
неявных (возможность счета с большими
шагами по времени)
 .
.
Одна из таких схем (используется при наличии двух пространственных переменных) – это схема направлена или может называться продольно-поперечная.
Суть схемы: шаг
 делится на два полушага. На первом
полушаге вторая производная по одной
из коэффициентов
делится на два полушага. На первом
полушаге вторая производная по одной
из коэффициентов
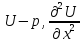 аппроксимируют неявно на слое
аппроксимируют неявно на слое
 , а другая вторая производная, в данном
случае ,
, а другая вторая производная, в данном
случае ,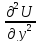 ,
аппроксимируют на слое
,
аппроксимируют на слое
 явно. На втором полушаге, наоборот,
неявная аппроксимация используется
только по направлению
явно. На втором полушаге, наоборот,
неявная аппроксимация используется
только по направлению
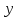 .
.
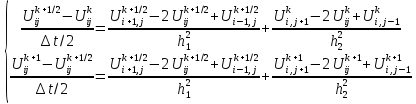
Эти уравнения
можно записать в виде систем линейных
алгебраических уравнений относительно
искомых функций соответственно в узлах
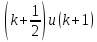 слоев:
слоев:
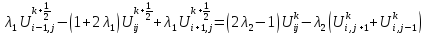
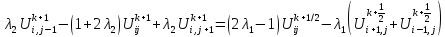
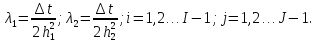
К этим системам
необходимо добавить начальное условие
 и граничные условия на каждом из этих
дробных по времени шагов.
и граничные условия на каждом из этих
дробных по времени шагов.
Матрицы этих систем
уже трехдиагональны. Здесь может быть
использован метод прогонки. При этом
вначале рассчитываются значения для
слоя
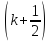 ,
а затем
,
а затем
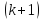 .
Видно, что диагональные элементы матрицы
преобладают, поэтому обеспечиваются
условия устойчивости прогонки. Это
также обеспечивает существование и
единственность решения. Приведенная
схема, безусловно, устойчива и сходится
со скоростью
.
Видно, что диагональные элементы матрицы
преобладают, поэтому обеспечиваются
условия устойчивости прогонки. Это
также обеспечивает существование и
единственность решения. Приведенная
схема, безусловно, устойчива и сходится
со скоростью
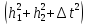 .
Для случая трех и более пространственных
переменных она не обобщается.
.
Для случая трех и более пространственных
переменных она не обобщается.
Здесь на каждом шаге по времени вводятся промежуточные этапы, на каждом этапе записывается одномерная аппроксимация по одному из пространственных направлений. То есть многомерная задача расщепляется на последовательность одномерных задач по каждой из координат. Такие схемы называются схемы с расщеплением.
В таких схемах отсутствует аппроксимация на промежуточных этапах, так как используемые одномерные разностные схемы не аппроксимируют исходное уравнение.
Однако здесь имеет место суммарная аппроксимация на слоях с целыми номерами, такая суммарная аппроксимация называется аддитивной.
Схема расщепления для двумерного уравнения теплопроводности.


Схема, безусловно,
устойчива и сходится со скоростью
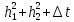 .
.
Эта схема легко обобщается на случай произвольного числа переменных. Естественно каждая новая переменная требует введения одного промежуточного этапа на каждом шаге по времени.
Это схема фактически
представляет собой двукратную неявную
схему для одномерного уравнения
теплопроводности. На первом этапе
находятся вспомогательные значения
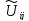 ,
а на втором искомые значения функции
,
а на втором искомые значения функции
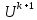 .
.

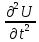 аппроксимируем
по трех точечному шаблону на слоях
аппроксимируем
по трех точечному шаблону на слоях
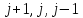
 заменяем полу
суммой аппроксимаций на
заменяем полу
суммой аппроксимаций на
 слоях. Получаем:
слоях. Получаем: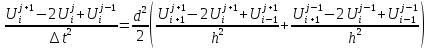
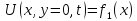
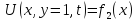
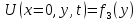
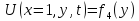
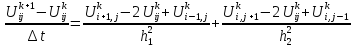
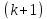 :
: