
Справедлива теорема:
Если дифференциальная задача (1) поставлена корректно, если разностная схема (2) также является корректной и аппроксимирует исходную задачу (1) – тогда решение разностной задачи (2) сходится к решению исходной задачи (1), причем порядок точности совпадает с порядком аппроксимации.
Значение этой теоремы в том, что она позволяет разделить изучение сходимости на два отдельных этапа: доказательство аппроксимации и доказательство устойчивости.
Последнее является более сложным этапом.
Как уже отмечалось,
если
 аппроксимирует LU,
то возникает погрешность (невязка) δ
аппроксимирует LU,
то возникает погрешность (невязка) δ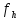 =LU
-
=LU
-
 ,
которая стремится к нулю при h->0.
,
которая стремится к нулю при h->0.
LU = f(x);
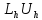 =
=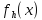 ;
LU -
;
LU -
 =
=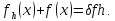
В случае аппроксимации
можно считать, что уравнение (2) которому
удовлетворяет
 получается из уравнения LU
= f,(1)
путем прибавления некоторой малой(при
помощи h)
добавки
получается из уравнения LU
= f,(1)
путем прибавления некоторой малой(при
помощи h)
добавки
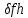 .
Следовательно если решение уравнения
устойчиво относительно возмущения
правой части, то есть мало изменяется
при малом изменении правой части, то
решение уравнения (1) и (2) будут отличаться
мало, так что из аппроксимации
.
Следовательно если решение уравнения
устойчиво относительно возмущения
правой части, то есть мало изменяется
при малом изменении правой части, то
решение уравнения (1) и (2) будут отличаться
мало, так что из аппроксимации
 следует сходимость
следует сходимость
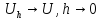 .
.
Таким образом трудный вопрос сходимости разбивается на два более простых: 1) Имеет ли место аппроксимация задачи (2) задачей (1); 2)Устойчива ли задача 2).
Отсюда вывод – нужно выбирать такие разностные вычислительные схемы (из множества возможных способов аппроксимации), которые являются устойчивыми.
То есть условие аппроксимации: уменьшение ошибок при h->0 LUh - > U – недостаточно, нужно еще устойчивость разностной схемы.
Эллиптические уравнения(например Пуассона).
Здесь нет времени, нет эволюции. Метод гармоник не используется, так как он использует слоистый по времени характер задачи и в конечном счете изучает эволюцию начального возмущения во времени.
В эллиптических уравнениях непосредственно проверяется
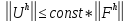
Здесь вводится вспомогательная функция R и доказывается, что разностная схема(2-го порядка аппроксимации производных) по каждой переменной устойчива.
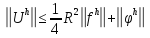 .
.
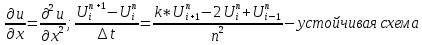
U =
U(t)
U =
U(t,x) -> U =
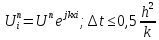

δ
Каждая гармоника:
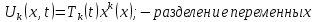
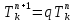 ;
;
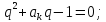 один из корней по модулю >1 поэтому при
достаточно больших n
в решении могут присутствовать сколь
угодно большие гармоники.
один из корней по модулю >1 поэтому при
достаточно больших n
в решении могут присутствовать сколь
угодно большие гармоники.
Устойчивость разностных схем.
Устойчивость линейных разностных схем:
 =
=
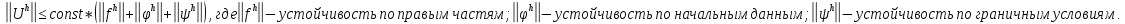
Метод гармоник (для эволюционных, то есть зависящих от времени задач)
Упрощения: а) правые части равны нулю;
б) отвлекаемся от краевых условий;
В этих условиях: частные решения разностных уравнений имеют вид гармоник

Условие устойчивости сводится к требованию ограниченности амплитуды этих гармоник.
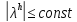 (10.7)
(10.7)
Для каждой схемы будет естественно своя зависимость λ = λ (∆t,h,ωh)
Проверка
условия (10.7) эквивалентна проверке
условия ( ):
):
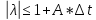 ,
где A=const
– условие Неймана устойчивости разностных
схем для эволюционных задач.
,
где A=const
– условие Неймана устойчивости разностных
схем для эволюционных задач.
По существу это проверка устойчивости по начальным (что является определяющим большей частью для эволюционных задач). Кстати для них получается
∆t
≤ 0,5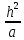
Мерой
малости погрешности аппроксимации
служит порядок разностной схемы. Порядок
«p»
означает, что при малых ∆t
погрешность аппроксимации пропорциональна
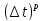 .
.
Устойчивость
связана с
изменением ошибки в процессе счета. От
разностной схемы будет мало пользы,
если даже малые погрешности аппроксимации
и округления будут быстро нарастать с
количеством шагов во времени. Это
нарастание может исказить решение.
«Численный метод устойчив, если на любой
стадии вычислительного процесса малая
ошибка приводит к меньшей конечной
ошибке». Пусть величина ошибки на n
– м шаге
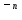 ,
а на (n+1)
-
,
а на (n+1)
-
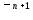 ,
тогда должно быть
,
тогда должно быть
 ,
то есть если
,
то есть если
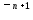 =g
=g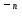 ,
то должно быть:
,
то должно быть:
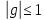 .
.
В принципе задачи могут иметь нарастающие решения (например по экспоненте). В этом случае можно допустить неограниченное нарастание ошибки, при условии, что последняя меньше растущего решения. Этот случай носит частный характер, и мы его в дальнейшем исключим.
Эффективность – характеризуется полным числом арифметических, логических и обменных операций, выполняемых центральным процессором для получения решения. Здесь могут быть компромиссы – например, между точностью решения и эффективностью.
__________________________________для уравнения в частных производных(на примере уравнения диффузии).
Уравнения в частных производных.
Абстрактные понятия сплошных сред и непрерывных полей находят широкое применение в физике:
- В классической электродинамике уравнения Максвелла формируются с помощью определения непрерывных функций источника;
- твердое тело часто для простоты трактуется как сплошное;
- разнообразные среды(жидкости, газы, плазма, галактическое вещество) – можно трактовать как сплошные среды.
Исходя из этих представлений, в пространстве и времени определяют непрерывные функции(которые описывают свойства среды), и применяя количественные законы физики (часто законы сохранения – импульса, заряда массы) получают уравнения в частных производных, связывающие свойства среды в пространстве и времени.
Уравнения в частных производных, вытекающие из этих идей называют консервативными.
Уравнение диффузии часто появляются при описании переноса частицы, импульса или энергии. В частности, оно описывает распределение температуры в твердом теле, где в классическом случае энергия переносится посредством теплопроводности.
По закону сохранения энергии скорость изменения в объеме V должна равняться потоку энергии q через поверхность S данного объема V:
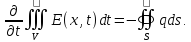
Применяя теорему -Гаусса к правой части получим
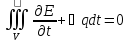
Пусть плотность энергии E пропорциональна температуре Е, получим уравнение диффузии:
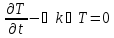 ,
k
– коэффициент теплопроводности.
,
k
– коэффициент теплопроводности.
В одномерном случае
 ,
где U
может быть
,
где U
может быть
В момент времени
t=o
начальные условия определяют зависимую
переменную на пространственной сетке
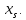
Допустим мы используем простейший путь – явный метод первого порядка – аналогичный методу Эйлера для обыкновенных дифференциальных уравнений. Пусть шаг по времени равен ∆t, в пространстве h. Тогда
 .
.
Здесь верхний индекс относится к шагу по времени, а нижний индекс i относится к шагу в пространстве. Пространство – временная сетка имеет вид:
То есть пространственная производная относится к определенному моменту времени (n). Рассмотрим точность, устойчивость и эффективность данной схемы, используя идеи, развитые для обыкновенных дифференциальных уравнений, добавив представление о фурье - модах или фурье – гармониках. Дело в том, что уравнения в частных производных связывают точки в пространстве и времени и простые линейные свойства уравнений в частных производных или их систем можно установить, исследуя поведение волны в пространстве и времени.
Считаем, что фурье
мода имеет вид: U(x,t)
=
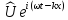 ,
где ω
– частота, k
=
,
где ω
– частота, k
=
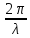 ,
λ
– длина волны – удовлетворяет уравнению
в частных производных. Частота ω
– может быть действительной (тогда
колебательный или волновой процесс), ω
– может быть комплексной, тогда затухающий
или нарастающий волновой процесс.
,
λ
– длина волны – удовлетворяет уравнению
в частных производных. Частота ω
– может быть действительной (тогда
колебательный или волновой процесс), ω
– может быть комплексной, тогда затухающий
или нарастающий волновой процесс.
В разностном решении задачи с начальными условиями нас интересуют временные масштабы задачи и их зависимость от длины волны, для различных физических процессов.
следуя общему подходу к анализу устойчивости схем, найдем множитель q (перехода) (или в более сложных случаях матрицу перехода) для фурье – моды:
U
=
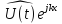 .
.
Подставим в разностное уравнение
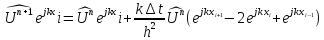
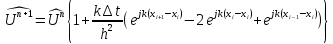
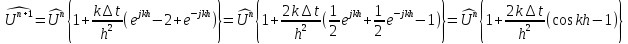 .
.
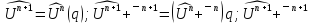 =
=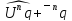 ;
;
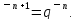
q
=
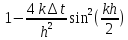
должно
быть
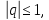 то есть
то есть
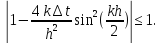 Выбираем максимальное значение sin
и тогда
Выбираем максимальное значение sin
и тогда
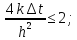
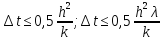
То есть связь временного шага ____________.
Этот
результат можно пояснить физически.
Максимальный допустимый шаг по времени
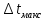 равен времени диффузии на характерной
длине h.
равен времени диффузии на характерной
длине h.
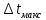 -
время распространения и _______ вдоль длины
h.
И если сходимость распространения
______ очень мала =
-
время распространения и _______ вдоль длины
h.
И если сходимость распространения
______ очень мала =
 то
можно ожидать катастрофических
результатов.
то
можно ожидать катастрофических
результатов.
Для определения
точности метода получают дисперсионное
соотношение для фурье – моды, для
разностной схемы и для дифференциального
уравнения. В
пределе при ∆t
->0 и больших
длинах волн они должны совпадать.
Интересно, что для уравнения переноса
 анализ, с использованием фурье – моды
приводит к комплексному q
и оказывается, что разностная схема(схема
первого порядка) неустойчива
при любых ∆t!!
анализ, с использованием фурье – моды
приводит к комплексному q
и оказывается, что разностная схема(схема
первого порядка) неустойчива
при любых ∆t!!
У Поттера приведены схемы и результаты анализа их устойчивости.
