Вариационные исчисления

Для функционала

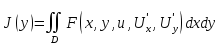
Уравнение Эйлера имеет вид:

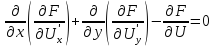
Существует и обратный переход на основе следующей теоремы:

Пусть L-симметричный оператор, определенный и положительный, в классе непрерывных в некоторой области функций, имеющих непрерывные производные, а Ф(U) – функционального вида:

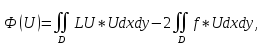
где f – правая часть уравнения (8)

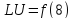
краевые условия

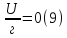
Если краевая задача (8), (9) с однородными граничными условиями имеет решение, то решение дает min функционалу Ф(U).

Обратно: Если существует функция, дающая минимум функционалу Ф(U), то эта функция является решением (5)

Вариационные методы

Это приближенные методы решения дифференциальных уравнений. Известно, что состояние многих физических объектов управляются так называемыми минимальными принципами. Например, постоянная равновесия механической системы есть положение, отвечающее минимальной потенциальной энергии.

В связи с этим проблема решения краевой задачи для дифференциального уравнения данной механической системы оказывается в общем эквивалентной проблеме нахождения функции, дающей минимум 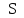, которым выражается потенциальная энергия системы.

Математически проблема решения краевой задачи для дифференциального уравнения эквивалентна задаче вариационного исчисления о минимуме интеграла, для которого данное дифференциальное уравнение служит уравнением Эйлера-Лагранжа. Рассмотрим это доказательство:

Итак, ознакомимся с основными идеями вариационного исчисления, а также формулами, которые пригодятся в дальнейшем.

Рассмотрим интеграл

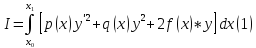
Он получает для каждой функции 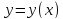, заданной для 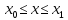какое-то определенное значение. В таких случаях говорят, что величина интеграла представляет функционал (то есть зависит от функции).

Поставим задачу: Найти кривую 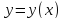, проходящую через заданные точк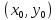и и 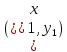и дающую минимальное значение .

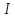Пусть есть уравнения 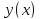, дающая минимальное значение . Пусть 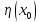- производная функция, непрерывная со своей производной и обращенная в 0 на концах x: .

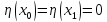Тогда функция 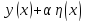удовлетворяет в точках и тем же условиям, что 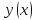и и при сколь угодно близка к .

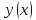При этом так как 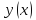дает минимальное значение при будет:

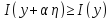
Таким образом интеграл как функция α, при имеет минимум, а поэтому

Найдем эту производную:

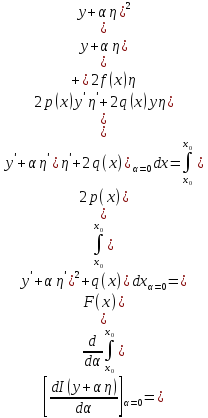
То есть последнее выражение должно быть =0 при любом 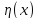удовлетворяющей нулю на границах.

Выражение 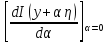называют вариацией интеграла и обозначают .

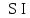Теперь можно сказать: для того, чтобы функция давала минимальное значение 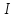, необходимо, чтобы его вариация равнялась нулю: 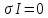при любой .

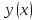Возьмемся за выражение

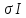
Проинтегрируем по частям первое слагаемое интеграла (3):

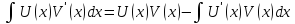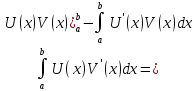– для неопределенного интеграла

– для определенного интеграла

В итоге примет вид:

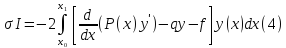
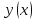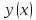Это выражение должно быть = 0 для любой . Это возможно лишь в том случае, если функция удовлетворяет дифференциальному уравнению:

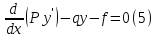
Уравнение, которому удовлетворяют экстремальные кривые, называется уравнением Эйлера для данной вариационной проблемы.

В данном случае для задачи минимума интеграла (1) уравнением Эйлера служит уравнение (5), то есть так называемое сопряженное уравнение второго порядка.

Общее решение уравнения (5) содержит в своем составе две производных постоянных.

Метод, с помощью которого мы получили уравнение Эйлера для интеграла (1) является общим и с незначительными изменениями применим к различным другим задачам.

Так, для так называемой простейшей задачи вариационного исчисления о минимуме интеграла 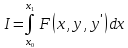, получим уравнение Эйлера:

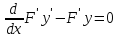
Вариационные задачи, приводящие к уравнению Лапласа и Пуассона.

Рассмотрим задачу с минимальным значением :

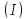, где D ограничен контуром Г.

Формулировка задачи: Найти функцию 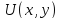, непрерывную в D внести с частными производными первого и второго порядка, принимающую на контуре Г заданные значения: 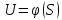на Г и дающую 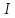минимальное значение.

Найдем опять необходимые условия

Пусть 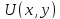дает минимальное значение 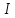. Рассмотрим функцию , где 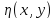- равна нулю по Г и непрерывна в месте с производными первого и второго порядков.

Как и ранее убеждаемся, что в таком случае вариация должна быть равна нулю.

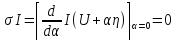
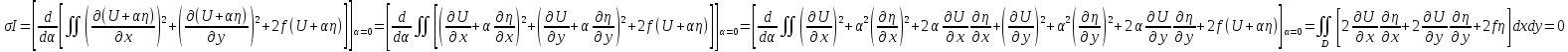
или же

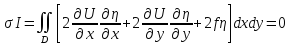
В выражении для 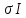преобразуем первое для члена с помощью формулы Грина:

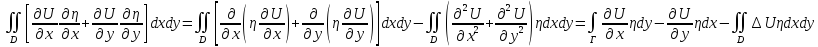
Так как по предположению 𝜂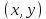 на Г равен нулю, то остается только второй интеграл и тогда для получим

.

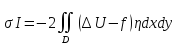Так как должно быть при любом 𝜂, то это значит

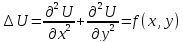
Таким образом, уравнением Эйлера в данном случае оказалось уравнение Пуассона.

Мы видим, что решение граничных задач для различных типов уравнений обыкновенных и в частных производных будет найдено, если будет решена задача о минимуме того или иного интеграла.

Для решения этой последней задачи были предложены в 1908 году метод Ритца, а в 1915 году метод Галеркина ( ещё более универсальный )

Основная идея метода Ритца

Рассмотрим общую задачу о минимуме двойного интеграла

,

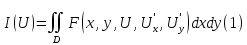при условии 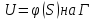, где Г – контур D (2)

Пусть 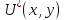– есть точное решение задачи, а 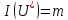значение минимума

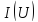
Для нахождения функции дающее не точное, а приближенное значение 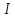близкое к 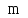предложен такой метод

Эти соображения верны и в других задачах.

Так, для общей задачи о минимуме SS:

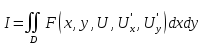
При заданных граничных условиях 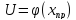- всегда можно свести к нулевому.

Получаем уравнение Эйлера в виде:

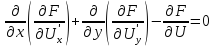
Задача о минимуме интеграла

имеет уравнением Эйлера самосопряженное уравнение эллиптического типа:

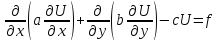
содержащее как частный случай уравнение Пуассона

Рассмотрим семейство функций, зависящих от нескольких параметров

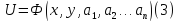
и такое, что при всех значениях параметров удовлетворяет условию (2).

Найдем среди семейства такую функцию, которая дает минимум интегралу . Это уже более легкая задача. Для этого подставив в (1) вместо 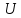, выражение (3) и выполнив необходимые дифференцирования и интегрирования, увидим, что 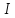превратится в функцию 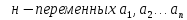. 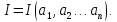Чтобы получить минимум, числа 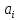должны удовлетворять системе уравнений

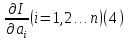
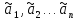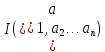Пусть решения этой системы, эти значения и дадут – абсолютный минимум.

Таким образом, мы получим требуемое приближенное решение. Причем практически его получить достаточно легко, то есть, обычно в интеграле 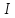подынтегральное выражение – многочлен второй степени относительно 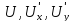; а семейство (3) обычно берется линейно зависящим от 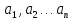, поэтому уравнение (4) обычно первой степени, при этом невелико: 2,3,4,5, а часто .

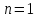Как теперь получить сколь угодно близкое приближенное к действительному минимуму m.

Для этой цели нужно рассмотреть ряд семейств функций 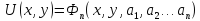. Каждое из которых шире предыдущего в результате добавления дополнительного параметра. Так же доказывается, что с ростом и минимум не убывает.

Идея основная метода Галеркина

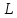Пусть ищется решение уравнения где - некоторый дифференциальный оператор с двумя переменными. Решение должно удовлетворять однородным граничным условиям.

Приближенное решение имеем в виде:

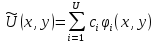
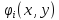
где 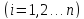- некоторая система заранее выбранных функций, удовлетворяющих тем же граничным условиям, а 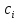- неопределенные коэффициенты.

Полнота системы семейств (6) состоит в том, что любая ______ функция может быть сколь угодно точно аппроксимирована вместе с частными производными посредством функций из данных семейств. Полнота - если к семейству функций нельзя добавить отличную от нуля функцию, которая была бы ортогональна ко всем функциям семейства.

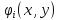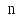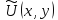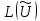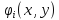
Можно считать всегда, что функции линейно-независимы и представляют первые функций некоторой системы функций полной в данной области. Для того, что точное решение _______ чтобы тождественна, а это равносильно требованию ортогональности выражения ко всем функциям системы 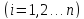. Имея в своем распоряжении только 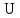постоянных 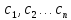мы можем, вообще удовлетворить лишь условиям ортогональности. Записав эти условия, приходим к системе уравнений:

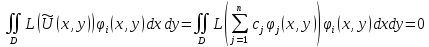
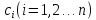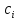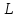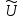Которая служит для определения коэффициентов . Найдя из этой линейной системы (в случае линейного оператора ) и подставляя их в получим требуемое решение

Метод Галеркина является универсальным, он применим к 1) эллиптическим, гиперболическим, параболическим уравнениям; 2) не связанным с вариационными проблемами. Однако, для задач, связанных с вариационными проблемами он в ряде случаев эквивалентен методу Ритца. Дает тоже приближенные решения, только быстрее.

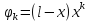,(k=1,2,…n)

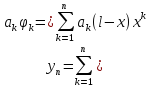Пусть k=4.

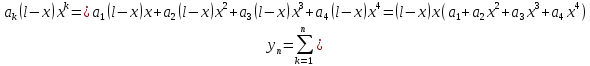
Применение методов Ритца и Галеркина к обыкновенным дифференциальным уравнениям.

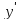Рассмотрим уравнение: L(y) = (p)-qy – f=0 (9)

При условиях 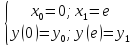(10)

Эта задача как мы видели может быть заменена задачей о ___ S:

I(y) = 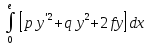(11)

при тех же условиях.

Удобнее в дальнейшем считать, что предельные условия однородны:

y(0)=y(e)=0 ()

Если бы это было не так, то мы добились бы этого вводя в уравнение (9) вместо y новую z:

y=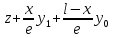; z=

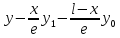
при x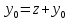=0: , z=0;

при x=e: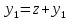, z=0;

Будем предполагать, что в промежутке (0≤x≤e): p(x)>0; q(x)>0. Зададимся теперь системой конкретных функций 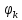(x) (k=1,2,…n), непрерывных в 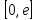вместе с первой производной, линейно независимых и удовлетворяющих условиям (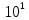). В качестве таких функций можно взять:

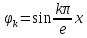или 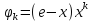, (k=1,2,…n)

По методу Ритца приближенное решение ищем в виде:

Подставим это выражение в интеграл (11):

I(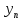) = 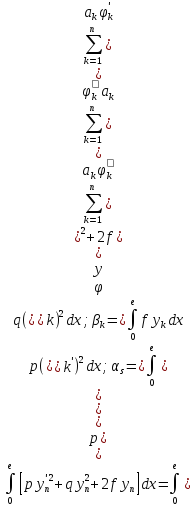(14)

s=1,2,…n

Дифференцируя (14) по as получаем:

=0

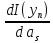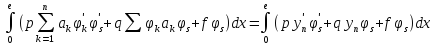=, s=1,2,…n.

Предадим этой системе другой вид, интегрируя первый член по частям и используя равенство 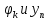нулю на концах

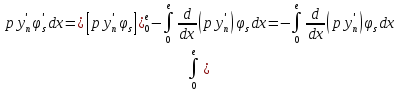
Тогда 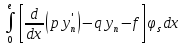=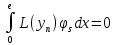, s=1,2,…n.

Видно, что эти уравнения не что иное как уравнения метода Галеркина.

Применение метода Ритца и Галеркина для решения уравнения в частных производных.

Рассмотрим задачу о решении уравнения Пуассона

L(u)=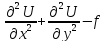=0 (28)

при условии u = 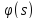на Г. (29)

Всегда можно это условие заменить на более простое

U=0 на Г. ()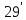

Для этого нужно построить любую функцию h(x, y), обращающуюся в 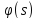на Г и тогда вводя вместо u правую неизвестную функцию z, определяемую формулой

u= z+ h(x, y); z= u-h(x, y)

Для функции z получим уже условие вида ()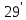

z=0 на Г.

Функция z. Также будет удовлетворять уравнению Пуассона лишь с другим свободным членом.

Итак наша задача равносильна задаче о минимуме интеграла

L(u)=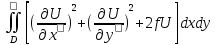 (30)

при нулевом условии u=0 на Г.

Для применения Ритца и Галеркина нужно иметь систему функций 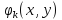; обращающихся в ноль на Г и полную в области D, то есть такую, что с помощью их линейных комбинаций можно приблизить любую функцию u(x, y) непрерывную с частными производными, удовлетворяющую условию ().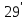

Если такая система избрана, то приближение по методу Ритца

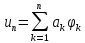
Подставляя это выражение вместо «n» в (30), получим:

I(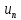)= 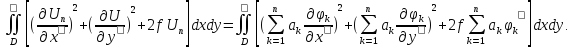Отсюда система, определяющая 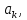может быть написана в виде

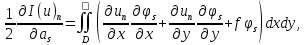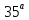() s=1,2,…n.

Придадим этой системе уравнений другой вид можно показать, что

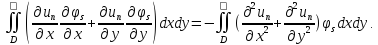
Применив это к правой части выражения (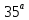), получим

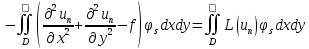
В качестве основной системы функций можно принять систему, составленную из произведений ω на различные степени x и y:

;; ; ;

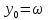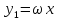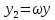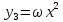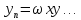
В некоторых случаях функция 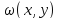определяется весьма просто. Например, для прямоугольника 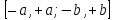можно принять 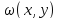=(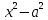)()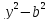; для окружности радиуса R с центром в начале .

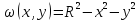Есть общие правила:

1. Если контур, ограниченный D допускает уравнение вида F(x, y)=0, где F- непрерывна вместе с частными производными, то .

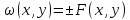2. Для случая выпуклого многоугольника, уравнения сторон которого 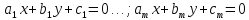можно принять:

=±()…….().

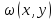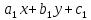Рассмотрим пример решения уравнения Пуассона методом Галеркина.

Дано: ∆u = -2, то есть f(x, y) = -2, u=0 на контуре Г. Это так называемая задача о кручении призматического стержня. Начало в центре прямоугольника. Прямоугольник – это сечение стержня.

Выбираем ω(x, y) = (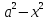)()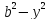. Решение ищем в виде u(x, y) = (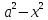)()(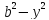)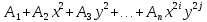. Пусть n=1, то есть U(x, y)= ()().

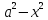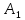Составим уравнение для определения

=

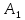
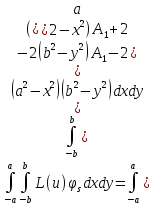
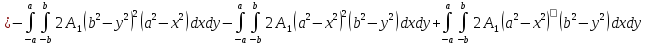
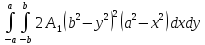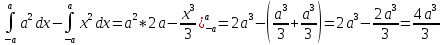
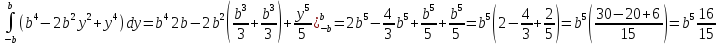
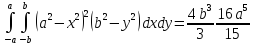
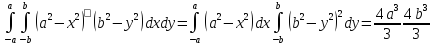
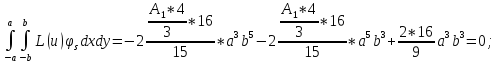
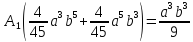
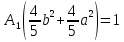
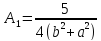
U=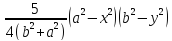

Главные особенности методов(Ритца и Галеркина).

1. Показывается, что краевую задачу, то есть включающую в себя обычное дифференциальное уравнение или дифференциальное уравнение в частных производных и некоторые граничные условия – можно свести к задаче поиска минимального определенного интеграла, для которого данное уравнение является уравнением Эйлера – Лагранжа;

2. Показывается, что при этом если краевая задача имеет отличные от нуля граничные условия, то всегда ее можно свести к задаче с нулевыми граничными условиями. При этом дифференциальный оператор не изменится, то есть вид левой части сохранится, а изменится только свободный член, то есть функция f(x, y), но это не имеет значения, то есть общность подхода сохранится;

3. Задача о поиске минимального интеграла оказывается более легкой, если воспользоваться методами Ритца и Галеркина.

Основные понятия теории разностных схем (аппроксимация, сходимость, устойчивость)

Здесь дается изложение основных понятий для линейных разностных схем самого общего вида (безотносительно к конкретной структуре исходного дифференциального уравнения и аппроксимацией его разностной схемы)

Пусть дана исходная дифференциальная задача:

LU(x)=f(x), (1)

где x ϵ G, G – область m- мерного пространства, L – линейный дифференциальный оператор. Граничные и начальные условия учтены в L и f(x). В общем случае (1) может быть многомерным и нестационарным, но L – всегда линейно. Вводится сетка - с шагом h.

После введения сетки 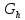следует заменить в (1) дифференциальный оператор L разностным оператором 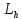, а f(x) сеточной функцией 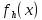. В результате получим систему разностных уравнений

(2)

Переходя от уравнения (1) к системе уравнений (2) мы по сути перешли от дифференциальной задачи – к дискретной разностной задаче. Иными словами мы аппроксимировали дифференциальную задачу дискретной разностной задачей. Но отсюда, вообще говоря, еще не следует близость решений этих двух задач.

Рассмотрим погрешности такого перехода (аппроксимации).

1)-я погрешность здесь возникает при переходе:

.

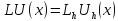-это погрешность аппроксимации дифференциального оператора

2)-я погрешность возникает при переходе:

f(x)->.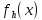

Дело в том, что поскольку разностный оператор не точно соответствует дифференциальному, то и в правой части (2) должно стоять не 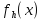, а другое значение, которое нам неизвестно.

Сумму погрешностей 1)+2) будем называть погрешностью аппроксимации дифференциальной задачи – разностной задачей.

Говорят, что разностная задача аппроксимирует исходную дифференциальную задачу, если при h>0 сумма погрешностей 1) и также стремится к нулю.

Разностная задача(схема) называется корректной,

1. если ее решение существует и единственно при любых правых частях (2), соответствующих заданному пространству (области);

2. если она устойчива.(устойчивость- означает непрерывную зависимость решения разностной задачи от ее правой части).

Главный вопрос для нас это – сходится ли решение разностной задачи к решению дифференциальной задачи.