
- •Оглавление
- •Высказывания. Примеры высказываний. Пропозициональные переменные. Определения основных логических операций.
- •Теорема о подстановке ппф вместо пропозициональной переменной в тождественно истинной формуле.
- •Теорема о существовании эквивалентной днф
- •Теорема о существовании эквивалентной кнф
- •Теоремы о виде тождественно ложной днф, тождественно истинной кнф
- •Понятия сднф, скнф. Построение сднф, скнф по таблице истинности данной формулы.
- •Построение сднф по данной днф.
- •Построение скнф по данной кнф
- •Условия существования скнф, сднф
- •Понятие логического следствия в ав. Содержательный пример.
- •Непротиворечивые (выполнимые) и противоречивые (невыполнимые) множества посылок. Примеры.
- •Установление факта логического следствия из данного множества посылок по таблице истинности.
- •Установление факта логического следствия из данного множества посылок путем определения совместности соответствующей системы логических уравнений.
- •Понятие алгебраической системы данной сигнатуры
- •Характерные черты алгоритма
- •Элементы модели алгоритма
- •Основные предположения об элементах модели алгоритма
- •Устройство машины Тьюринга
- •Комбинации машин Тьюринга: композиция
- •Комбинации машин Тьюринга: разветвление
- •Комбинации машин Тьюринга: разветвление с циклом.
- •Вычислимые по Тьюрингу функции.
- •Разрешимые (рекурсивные) множества. Пример. Рекурсивно перечислимые множества. Пример.
- •Алгоритмически неразрешимые проблемы. Пример. Тезис Тьюринга.
Понятие алгебраической системы данной сигнатуры
Алгебраической
системой
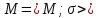 сигнатуры
сигнатуры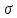 назовем алгебраическую систему
назовем алгебраическую систему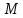 ,
в которой:
,
в которой:
Каждому n-местному предикатному символу из
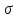 сопоставленn-местный
предикат из
сопоставленn-местный
предикат из ,
заданный на М.
,
заданный на М.Каждому n-местному функциональному символу из
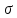 сопоставленаn-местная
функция из
сопоставленаn-местная
функция из ,
заданная на М.
,
заданная на М.Каждой предметной константе
 из
из сопоставлен элемент
сопоставлен элемент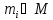
Свободные и связанные переменные. Термы, свободные для данной переменной в данной формуле.
Переменная называется свободной в ппф, если имеются свободные вхождения этой переменной в этой ппф.
Переменная называется связанной в ппф, если имеются связанные вхождения этой переменной в этой ппф.
Все свободные и связанные переменные обозначаются разными буквами.
Терм
 свободен для переменной
свободен для переменной в формуле
в формуле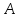 если никакое свободное вхождение
если никакое свободное вхождение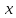 в
в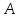 не находится в области действия никакого
квантора
не находится в области действия никакого
квантора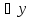 или
или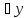 ,
где
,
где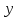 – переменная, входящая в
– переменная, входящая в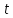 .
.
Значение терма данной сигнатуры в алгебраической системе той же сигнатуры. Пример.
Определим
значение терма
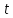 системы
системы ,
все предметные переменные которого
содержатся в наборе
,
все предметные переменные которого
содержатся в наборе в алгебраической системе
в алгебраической системе при значениях переменных
при значениях переменных соответственно следующим образом:
соответственно следующим образом:
Если
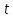 есть константа
есть константа ,
то значение
,
то значение есть значение
есть значение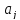
Если
 есть переменная
есть переменная ,
то значение
,
то значение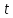 есть
есть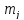
Если
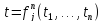 ,
а
,
а соответственно, то
соответственно, то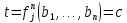 согласно функции
согласно функции
Пример:
Пусть
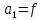 ,
тогда
,
тогда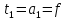
Значение ппф АП данной сигнатуры в алгебраической системе той же сигнатуры
Значение
 в алгебраической системе
в алгебраической системе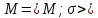 при
при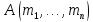 определим следующим образом:
определим следующим образом:
Если
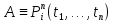 ,
то
,
то только если
только если
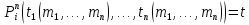 в
в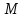 ,
иначе
,
иначе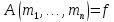
Если
 ,
то
,
то только если
только если и
и ,
иначе
,
иначе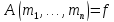
Если
 ,
то
,
то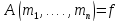 только если
только если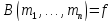 и
и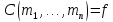 иначе
иначе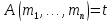
Если
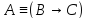 ,
то
,
то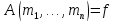 только если
только если и
и иначе
иначе
Если
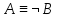 ,
то
,
то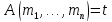 только если
только если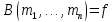 и наоборот.
и наоборот.Если
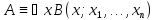 ,
то
,
то только если
только если для всех
для всех ,
иначе
,
иначе
Если
 ,
то
,
то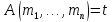 только если
только если хотя бы для одного
хотя бы для одного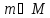 ,
иначе
,
иначе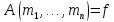
Кванторы
 и
и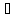 как обобщения логических связок & и
как обобщения логических связок & и .
.
Если М –
конечное основное множество алгебраической
системы
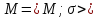 сигнатуры
сигнатуры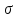 ,
,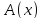 – ппф данной сигнатуры, то предложения
– ппф данной сигнатуры, то предложения и
и ,
где
,
где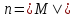 ,
имеют одно и то же значение.
,
имеют одно и то же значение.
Если М –
конечное основное множество алгебраической
системы
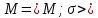 сигнатуры
сигнатуры ,
,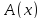 – ппф данной сигнатуры, то предложения
– ппф данной сигнатуры, то предложения и
и имеют
одно и то же значение.
имеют
одно и то же значение.
Выполнимые формулы АП. Пример.
Ппф
 сигнатуры
сигнатуры назовем выполнимой, если существует
такая алгебраическая система
назовем выполнимой, если существует
такая алгебраическая система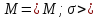 ,
что
,
что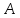 истинна в
истинна в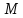 при некоторых значениях свободных
предметных переменных.
при некоторых значениях свободных
предметных переменных.
Пример:
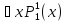 выполнима.
выполнима.
Тождественно истинные формулы АП. Пример доказательства тождественной истинности.
Ппф
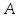 сигнатуры
сигнатуры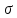 назовем тождественно истинной, если
назовем тождественно истинной, если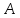 истинна в любой алгебраической системе
сигнатуры
истинна в любой алгебраической системе
сигнатуры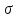 при любых значениях свободных предметных
переменных.
при любых значениях свободных предметных
переменных.
Пример:
 – тождественно истинная.
– тождественно истинная.
Доказательство производится методом от противного, тоесть
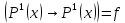 такое возможно лишь при
такое возможно лишь при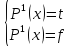 ,
что невозможно.
,
что невозможно.
Эквивалентные формулы АП. Пример.
Две ппф
алгебры предикатов
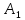 и
и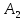 сигнатуры
сигнатуры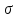 называются эквивалентными, если они
принимают одинаковые значения (tилиf) в любых алгебраических
системах данной сигнатуры. Факт
эквивалентности ппф
называются эквивалентными, если они
принимают одинаковые значения (tилиf) в любых алгебраических
системах данной сигнатуры. Факт
эквивалентности ппф и
и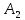 записывается в виде
записывается в виде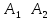 .
.
Если они
эквивалентны только в какой-то
алгебраической системе
 ,
то факт эквивалентности записывается
как
,
то факт эквивалентности записывается
как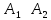 (а
внизу такая хуевинка
(а
внизу такая хуевинка
Пример:
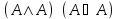 в любой алгебраической системе
в любой алгебраической системе
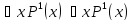 эквивалентны лишь в системе с одноместной
базой (вместоxТОЛЬКОtили ТОЛЬКОf)
эквивалентны лишь в системе с одноместной
базой (вместоxТОЛЬКОtили ТОЛЬКОf)
Теорема о замене подформулы на эквивалентную подформулу в ппф алгебры предикатов.
Пусть
 – подформула
– подформула ,
, ,
тогда
,
тогда
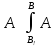
Теорема о подстановке ппф вместо атомной формулы в эквивалентные ппф алгебры предикатов
Пусть
 - ппф сигнатуры
- ппф сигнатуры ,
, – атомная формула, тогда если
– атомная формула, тогда если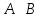

Пренексные нормальные формы. Теорема о существовании эквивалентной пнф: алгоритм получения эквивалентной пнф.
Пусть Qобозначает некоторый квантор или
или .
Тогда ппф вида
.
Тогда ппф вида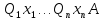 ,
где
,
где – бескванторная формула, называетсяпренексной нормальной формой.
– бескванторная формула, называетсяпренексной нормальной формой.
Теорема о существовании:
Для любой ппф алгебры предикатов существует эквивалентная ей пренексная форма.
Алгоритм получения:
Исключаем
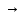
Продвигаем
 до атома.
до атома.Переименовываем связанные переменные
Вынесим кванторы
Сколемовская стандартная форма (ссф): основная теорема, функции Сколема.
Пренексная
форма вида
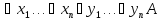 называется сколемовской.
называется сколемовской.
Основная теорема:
Пусть
предложение
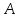 сигнатуры
сигнатуры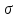 имеет вид
имеет вид

Также пусть
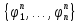 –nместные функциональные
символы.
–nместные функциональные
символы.
Пусть
предложение
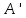 сигнатуры
сигнатуры имеет вид
имеет вид
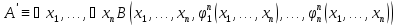
Тогда для
любой алгебраической системы
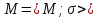 существует алгебраическая система
существует алгебраическая система такая, что значение
такая, что значение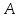 в
в совпадает со значением
совпадает со значением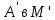 .
.
 - обогащение
- обогащение ,
а
,
а – обеднение
– обеднение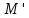 .
Функции
.
Функции ,
вводимые вместо кванторов
,
вводимые вместо кванторов ,
называются функциями Сколема.
,
называются функциями Сколема.
Сколемовская стандартная форма (ссф): следствие основной теоремы.
Пренексная
форма вида
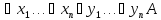 называется сколемовской.
называется сколемовской.
Следствие:
Для любого
предложения
 сигнатуры
сигнатуры существует некоторое
существует некоторое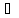 предложение
предложение расширенной сигнатуры
расширенной сигнатуры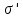 ,
полученное добавлением к
,
полученное добавлением к новых функциональных символов, и
обладающее свойством: для любой
алгебраической системы
новых функциональных символов, и
обладающее свойством: для любой
алгебраической системы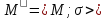 существует обогащение
существует обогащение такое, что значение
такое, что значение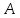 в
в совпадает со значением
совпадает со значением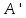 в
в .
.
Сколемовская стандартная форма(ссф): процедура построения, алгоритм Сколема.
Алгоритм Сколема:
Представить исходное предложение
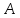 в виде пнф
в виде пнфНайти квантор

Если квантор
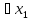 самый первый, то заменить все вхождения
самый первый, то заменить все вхождения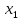 на
на
Если нет, то заменить все вхождения
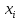 на
на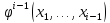
Повторять до усеру.
Понятие логического следствия в АП. Пример.
Ппф
 сигнатуры
сигнатуры называется логическим следствием
множества формул
называется логическим следствием
множества формул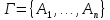 той же сигнатуры в алгебре предикатов,
если в любой алгебраической системе
той же сигнатуры в алгебре предикатов,
если в любой алгебраической системе ппф
ппф получает значениеtкаждый
раз, как каждая ппф ппф
получает значениеtкаждый
раз, как каждая ппф ппф принимает значениеtв
этой системе.
принимает значениеtв
этой системе.
Пример:
Пусть
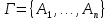 ,
, .
.
Рассмотрим
произвольную алгебраическую модель
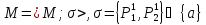 .
Пусть в этой модели
.
Пусть в этой модели ,
тогда
,
тогда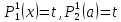 ,
значит
,
значит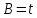 .
Значит
.
Значит .
.
Выполнимые и невыполнимые множества посылок в АП
Множество
посылок
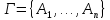 выполнимо в алгебре предикатов, если
найдется алгебраическая система
соответствующей сигнатуры такая, что
в базе этой системы существует набор
значений свободных переменных, на
котором все формулы из
выполнимо в алгебре предикатов, если
найдется алгебраическая система
соответствующей сигнатуры такая, что
в базе этой системы существует набор
значений свободных переменных, на
котором все формулы из принимают значениеt.
принимают значениеt.
Множество
посылок
 невыполнимо в АП, если в любой алгебраической
системе соответствующей сигнатуры для
любого набора значений свободных
предметных переменных найдется ппф
невыполнимо в АП, если в любой алгебраической
системе соответствующей сигнатуры для
любого набора значений свободных
предметных переменных найдется ппф ,
значение которой =f.
,
значение которой =f.
Понятие резольвенты в АВ. Пример.
Пусть
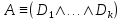 – кнф,
– кнф, – элементарные дизъюнкции (дизъюнкты).
– элементарные дизъюнкции (дизъюнкты).
Резольвентой
дизъюнктов
 назовем дизъюнкт
назовем дизъюнкт
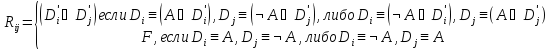
Теорема о свойстве резольвенты.
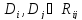 или
или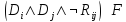
Основная теорема
Кнф
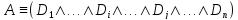 тождественно ложно тогда и только тогда,
когда тождественно ложна кнф
тождественно ложно тогда и только тогда,
когда тождественно ложна кнф
Формулировка принципа резолюции в АВ
Пусть
 - некоторое множество дизъюнктов и
пусть для
- некоторое множество дизъюнктов и
пусть для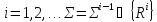 ,
где
,
где – резольвента некоторой пары дизъюнктов
из
– резольвента некоторой пары дизъюнктов
из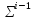 .
Тогда, если для некоторогоi
.
Тогда, если для некоторогоi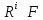 ,
то кнф
,
то кнф .
.
Схема применения принципа резолюции для доказательства факта логического следствия в АВ. Пример применения принципа резолюции для доказательства факта логического следствия.
Необходимо
определить, имеет ли место факт логического
следствия

Образуем ппф

Для
 строим эквивалентную ей кнф
строим эквивалентную ей кнф
Образуем
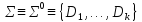 и применяем принцип резолюции. Если на
каком-то шагеi-1 получаем
«пустой дизъюнкт» - тождественно ложную
резольвенту
и применяем принцип резолюции. Если на
каком-то шагеi-1 получаем
«пустой дизъюнкт» - тождественно ложную
резольвенту ,
то
,
то
Пример:
Проверим
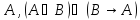
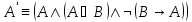

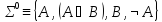 видим что
видим что образуют контрарную пару литер и дают
образуют контрарную пару литер и дают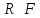 ,
значит
,
значит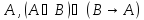
Схема построения модели алгоритма
Выделение основных свойств (характерных черт, присущих алгоритму)
Определение основных элементов модели, исходя из выделенных характерных черт.
Принятие основных предположений об элементах модели (установление основных ограничений)
В рамках принятых предположений построение и анализ конкретных моделей алгоритмов
Установление взаимосвязи между различными моделями алгоритмов.
