Министерство образования Республики Беларусь

Учреждение образования

«Белорусский государственный университет информатики и радиоэлектроники»

Факультет заочного обучения

Контрольная работа по дисциплине

«Дискретная математика»

Студента группы

Фамилия

Имя

Отчество

Зачётная книжка

Вариант 31

Проверил

Минск 2010

Вариант 31

1. В графе, представленном следующей матрицей смежности, найти все максимальные независимые множества

1 2 3 4 5 6 7 8

0 1 0 1 1 1 0 0 1

1 0 1 1 0 1 0 1 2

0 1 0 0 1 0 1 0 3

1 1 0 0 0 0 0 1 4

1 0 1 0 0 1 1 0 5

1 1 0 0 1 0 1 1 6

0 0 1 0 1 1 0 0 7

0 1 0 1 0 1 0 0 8

Решение

Независимое множество вершин - множество вершин графа такое, что любые две вершины в нем не смежны (никакая пара вершин не соединена ребром).

Воспользуемся матрицей смежности. К примеру, на пересечении 1-ой строки и 3-го столбца стоит число 0, значит, вершины 1 и 3 не смежны, т.е. образуют независимое множество вершин. Наоборот, на пересечении 1-ой строки и 2-го столбца стоит число 1, значит, вершины 1 и 2 смежны, т.е. не образуют независимое множество.

Таким же образом, пользуясь матрицей смежности и правилом лексикографического перебора, выпишем для данного графа все независимые множества:

{1,3}, {1,7}, {1,8}, {2,5}, {2,7}, {3,4}, {3,6}, {3,8}, {4,5}, {4,6}, {4,7}, {5,8}, {7,8}, {1,3,8}, {1,7,8}, {3,4,6}.

Независимое множество называется максимальным, когда нет другого независимого множества, в которое оно бы входило.

Выберем теперь из всех независимых множеств максимальные и запишем их:

{2,5}, {2,7}, {4,5}, {4,7}, {5,8}, {1,3,8}, {1,7,8}, {3,4,6}.

2. Получить минимальную систему ДНФ для следующей системы полностью определенных булевых функций:

, .

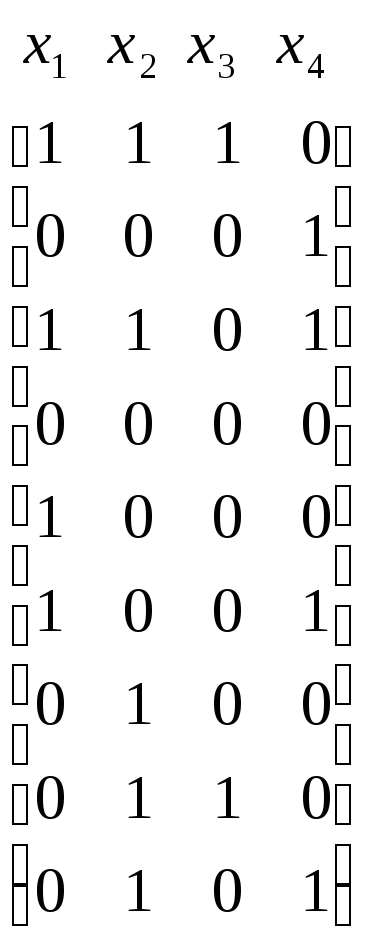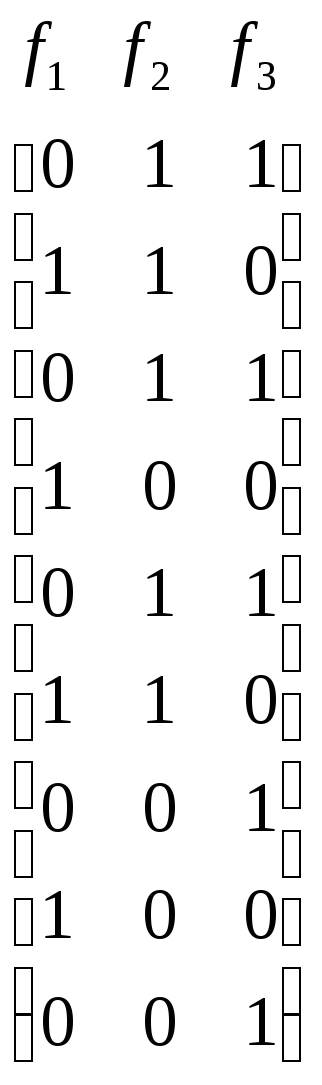Решение

Задача минимизации системы ДНФ формулируется следующим образом: для заданной системы булевых функций получить такую систему ДНФ, в которой общее число различных элементарных конъюнкций было бы минимальным.

Применим метод Квайна-МакКласки.

Для начала вспомним сведения из теории.

Пусть F – некоторая система булевых функций. Элементарная конъюнкция является обобщенной простой импликантой для множества булевых функций F  F, если она является импликантой для любой функции из F и перестает быть импликантой при удалении из нее любого литерала и не является импликантой ни для какой функции, не принадлежащей F.

Процесс минимизации системы ДНФ по данному методу состоит из двух этапов: 1) нахождение множества всех обобщенных простых импликант для заданной системы; 2) выделение из этого множества минимального подмножества, удовлетворяющего условию, что для всякой функции, принадлежащей заданной системе, можно из этого подмножества получить задающую ее ДНФ.

Исходная система булевых функций представлена в виде системы совершенных ДНФ, которая задана парой булевых матриц. Это матрица аргументов и матрица функций. Строки матрицы аргументов представляют конъюнкции максимального ранга, являющиеся членами заданных ДНФ. Другими словами, эти строки являются элементами булева пространства, на каждом из которых хотя бы одна функция заданной системы имеет значение 1. Столбцы матрицы функций соответствуют заданным функциям, и единицы в них показывают, какие конъюнкции принадлежат ДНФ соответствующей функции. То есть любая строка этой матрицы задает множество функций, имеющих значение 1 на наборе значений аргументов, представляемым одноименной строкой матрицы аргументов.

Первый этап выполняется с помощью простого склеивания. При этом учитываются характеристики импликант. Под характеристикой понимается множество функций, для которого данная конъюнкция является импликантой. Начальные значения характеристик задаются строками матрицы функций. Результату склеивания приписывается в качестве характеристики пересечение характеристик склеиваемых конъюнкций, которое получается поразрядной конъюнкцией соответствующих векторов. Естественно, что если результатом поразрядной конъюнкции является вектор, все компоненты которого нули, то результат склеивания не рассматривается.

Склеиваемым конъюнкциям приписывается знак «*», но приписывается он только тем конъюнкциям, характеристика которых совпадает с характеристикой результата склеивания.

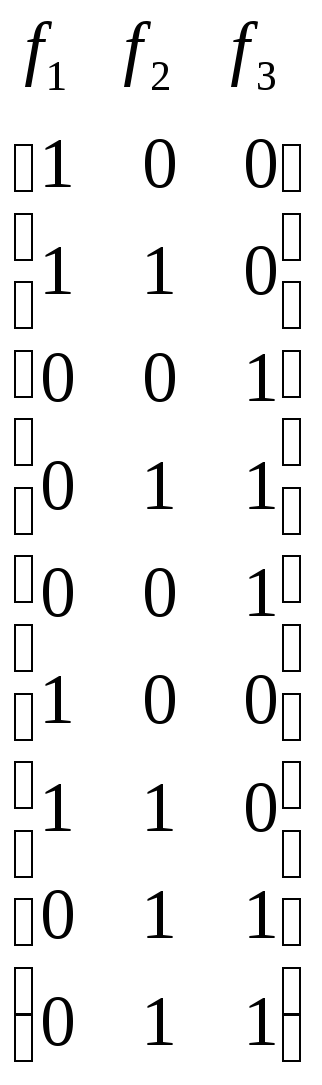
Для удобства сгруппируем исходные булевы векторы матрицы аргументов (и соответствующие им булевы векторы матрицы функций) в подмножества, состоящие из векторов, имеющих одинаковое число единиц, и упорядочим эти подмножества по возрастанию (или убыванию) числа единиц в векторе.

Получим

, .

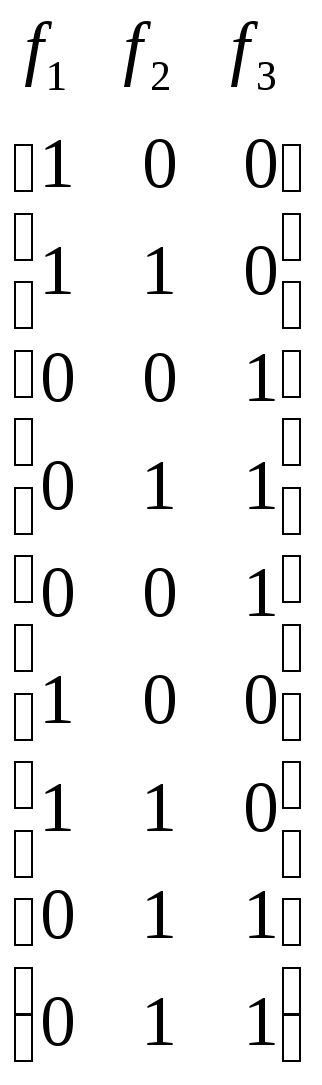Выполняем процесс простого склеивания, получаем следующую последовательность пар матриц:

; .

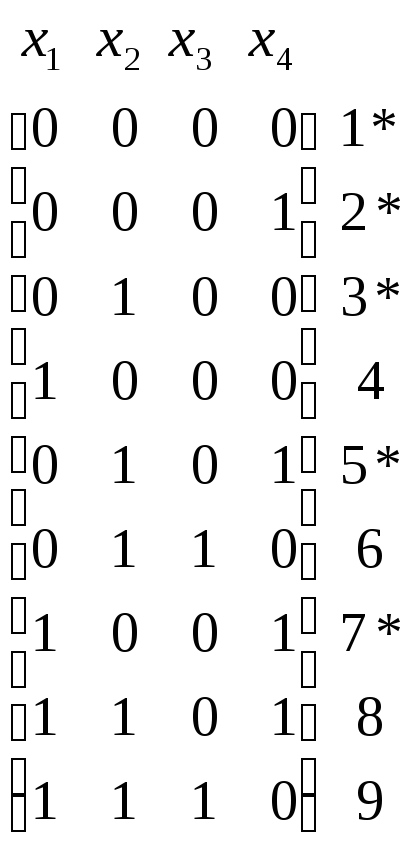
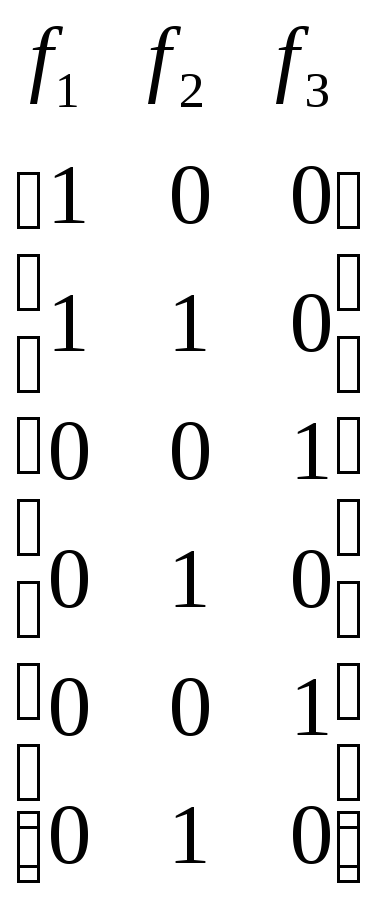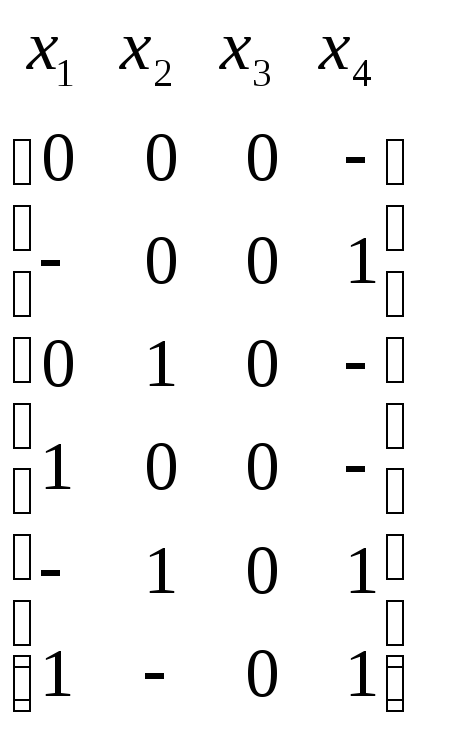
Полученную сокращенную систему ДНФ, которая содержит все обобщенные простые импликанты представим следующей парой матриц, где собраны строки, не отмеченные знаком «*»:

U = , V = .

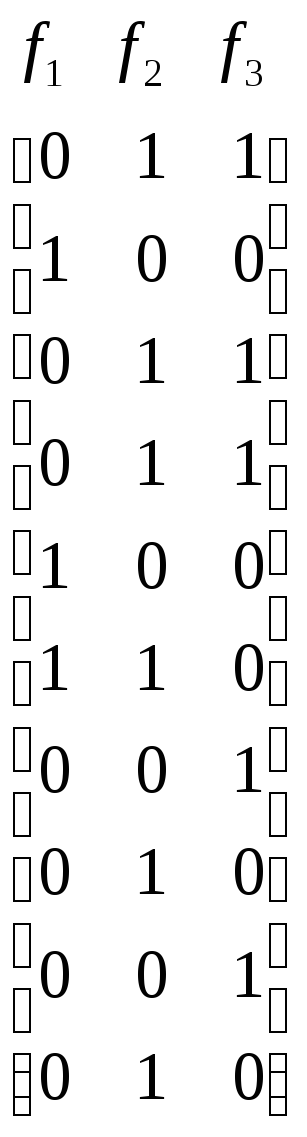Строки матрицы U представляют интервалы булева пространства аргументов. В матрице V единица в столбце f_i и j-й строке показывает, что на всем j-м интервале функция f_i имеет значение 1 (j-я конъюнкция входит в ДНФ функции f_i).

Рассмотрим теперь выполнение второго этапа минимизации, который сводится к задаче покрытия. Пара одноименных строк матриц U и V представляет множество пар вида (m_i, f_j), где m_i – элемент булева пространства аргументов, а f_j – функция, принимающая значение 1 на этом элементе. Интервал и его характеристика являются сомножителями декартова произведения, результат которого представляет собой множество с элементами вида (m_i, f_j). Очевидно, всего пар вида (m_i, f_j) в задании системы булевых функций столько, сколько единиц в исходной матрице функций. Необходимо из полученной совокупности интервалов выбрать минимум так, чтобы выбранные интервалы со своими характеристиками покрыли все множество пар (m_i, f_j) в задании исходной системы.

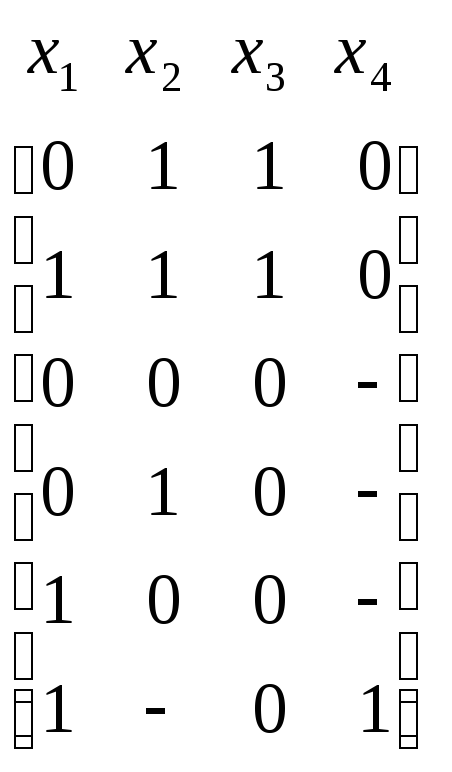
Для решения рассматриваемого примера построим следующую матрицу, строкам которой соответствуют пары строк матриц U и V, а столбцам – пары вида (m_i, f_j):

Здесь надо выбрать минимальное количество строк так, чтобы каждый столбец имел единицу хотя бы в одной из них.

Строка 2 является единственной строкой, которая покрывает столбец (6,f₁), строка 4 – единственной, которая покрывает столбцы (9,f₂) и (9,f₃), строка 5 – единственной, которая покрывает столбец (1,f₁), строка 7 – единственной, которая покрывает столбец (3,f₃). Все эти строки необходимо включить в кратчайшее покрытие.

Удалив эти строки и покрываемые ими столбцы, получим матрицу

Строки 8 и 10 составляют минимальное покрытие получившейся матрицы.

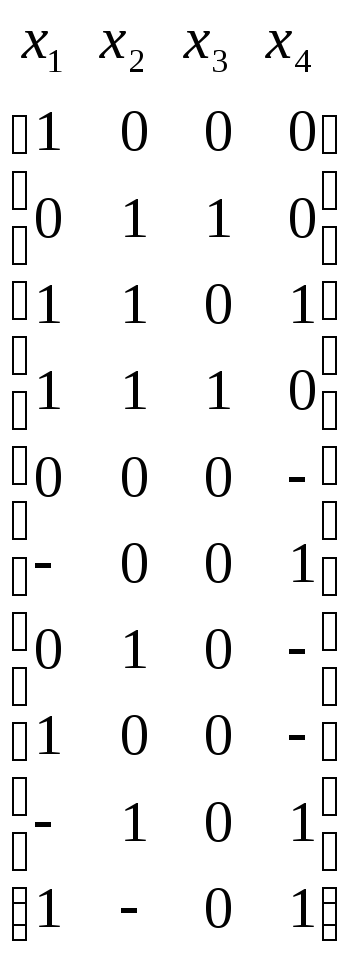
Таким образом, искомое кратчайшее покрытие составляют строки с номерами 2,4,5,7,8,10, а минимальная система ДНФ представляется матрицами

U = V=.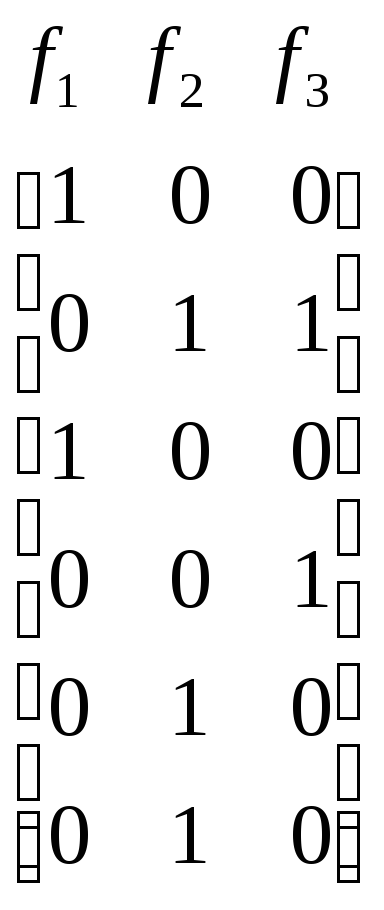

3. Закодировать с устранением влияния гонок состояния асинхронного автомата, заданного следующей таблицей переходов. Получить соответствующую минимальную систему ДНФ.

	00	01	10
1	1	1	3
2	-	2	3
3	1	3	3
4	5	2	4
5	5	2	4