КР №2 Вариан 7

Томский межвузовский центр дистанционного образования

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Кафедра автоматизированных систем управления (АСУ)

Контрольная работа №2

по дисциплине «Высшая математика»

г. Кызыл

2011 г

1. Даны координаты вершин треугольника А (1,3), В (2,8), С (6,6). Запишите общее уравнение прямой, на которой расположена медиана Аm ∆АВС

Решение:

Найдем координаты точки m – середины отрезка ВС:

m(4;7)

Уравнение АМ:

4x-4=3y-9

4x-3y+5=0 – общее уравнение Аm

Ответ: 4x-3y+5=0

2. Найдите координаты точки В, симметричной точке А(3,2) относительно прямой x+2y-2=0

Решение:

x+2y-2=0 →

Расстояние AM:

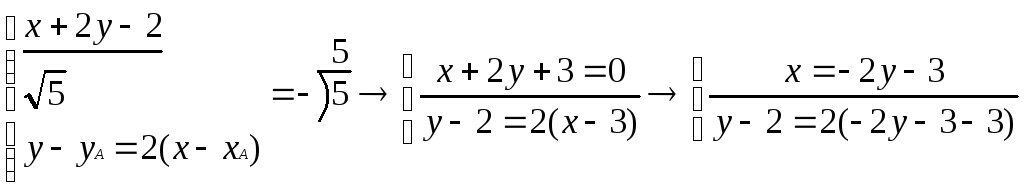
y-2=-4y-12

5y=-10

Ответ: В(1;-2)

3. Запишите общее уравнение плоскости, проходящей через точку М(2;-1) перпендикулярно двум плоскостям: x-2y+3t-2=0 и x+4y-2x+1=0

Решение:

Так как искомая плоскость перпендикулярна к данным плоскостям, то она параллельна их нормальным векторам ℓ₁(1;-2;3) и ℓ₂(1;4;-2) поэтому уравнение плоскости можно записать в виде:

(x-2) (4-12) – (y+1) (-2-3)+(t-1)(4+2)=0

-8(x-2)+5(y+1)+6(t-1)=0

8x-5y-6t-16-5+6=0

8x-5y-6t-15=0

Ответ: 8x-5y-6t-15=0

4. Найдите то значение параметра р₁ при котором прямые

и пересекаются.

Решение:

Запишем уравнение второй прямой в параметрическом виде:

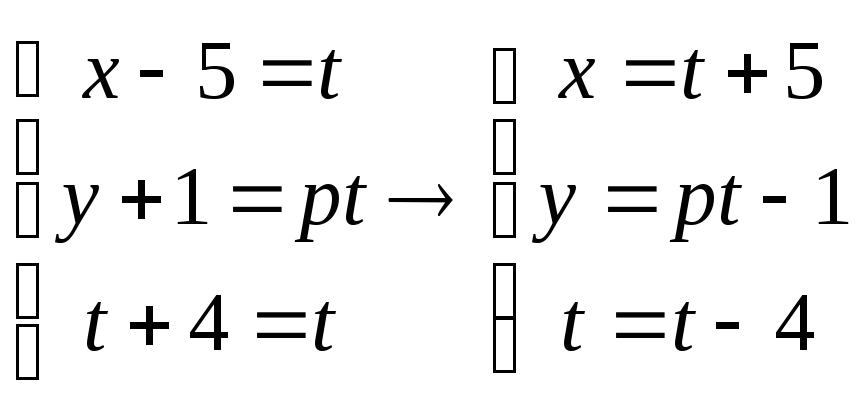
Условием пересечения двух прямых является выполнение условия (ζ₁- ζ₂, ℓ₁-ℓ₂)=0

ζ₁ = (-3;-2;6); ζ₂ = (5;-1;-4)

ℓ₁ = (2;3;-4); ℓ₂ =(1;р;1)

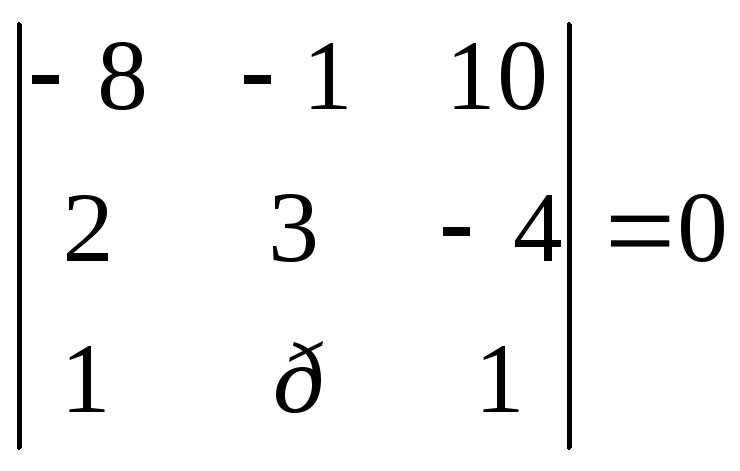
-24+4+20р-30+2-32р=0

12р=-48

р=-4

Ответ: р=-4

5. Найдите длину отрезка, отсекаемого от оси абсцисс плоскостью, проходящей через прямую

и точку М(1;1;0)

Решение:

Найдем уравнение плоскости

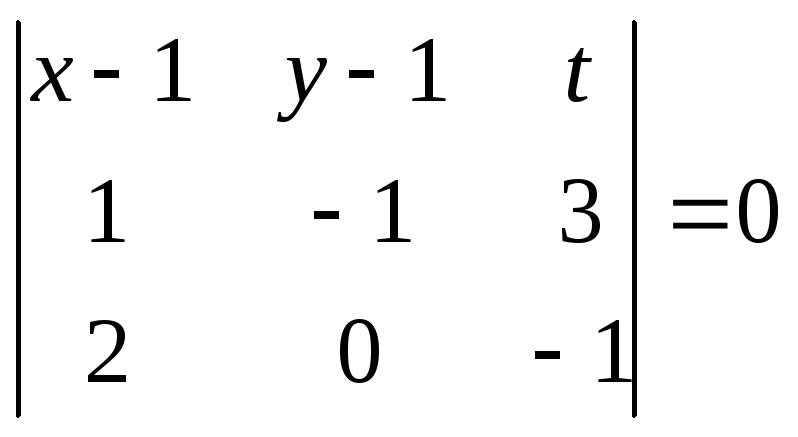
x-1+7(y-1)+2t=0

x+7y+2t-8=0

Точка пересечения плоскости с осью абсцисс имеет вид (х₀;0;0)

Найдем х₀, представив указанные координаты в уравнении плоскости:

х₀+7*0+2*0-8=0

х₀=8 - это и есть длинна отрезка, отсекаемого от оси абсцисс заданной плоскостью.

6. Найдите расстояние между плоскостями x-2y+2t+11=0 и x-2y+2t-25=0

Решение:

Возьмем на плоскости x-2y+2t+11=0 произвольную точку М(x₀,y₀,t₀) Пусть y₀=0, t₀=0. тогда x=-11 М(-11;0;0)

Расстояние от точки М до второй плоскости есть расстояние между плоскостями:

Ответ: 12

7. Найдите радиус сферы x²+y²+t²-2_x-2_y-6_t+λ=0, если известно, что она касается плоскости 3_x-2_y+6_t+23=0

Решение:

x²-2x+1+y²-2y+1+t²+6^t+9=11-λ

(x-1)²+(y-1)²+(y-3)²=11-λ

Центр сферы находиться в точке С(1;1;3). Радиус сферы есть расстояние от центра сферы – точки С до плоскости 3x-2y+6t+23=0

R=(ед.)

Ответ: R=6

8. Дана кривая x²+y²-8x-2y=47

8.1 Докажите что эта кривая окружность

8.2 Найдите координаты ее центра

8.3 Найдите ее радиус

Решение:

8.1 x²+y²-8x-2y=47

x²-8x+16-y²-2y+1=47-17

(x-4)²+(y-1)²-8² – окружность

8.2 Координаты центра (4;1)

8.3 Радиус окружности -8

9. Дана кривая 25х²-16y²+32y-416=0

9.1 Докажите что эта кривая гипербола

9.2 Найдите координаты ее центра симметрии

9.3 Найдите действительную и мнимую полуоси

9.4 Запишите уравнение фокальной оси

9.5 Постройте данную гиперболу

Решение:

9.1 25x²-16(y²-2y+1)=416-16

25x²-16(y-1)²=400

- гипербола

9.2 Центр симметрии гиперболы С(0;1)

9.3 Действительная полуось

Минимальная полуось

9.4 Уравнение фокальной оси: y=1

9.5

10. Дана кривая 9x²+16y²+27xy-40x+30y=0

10.1 Докажите что данная кривая парабола

10.2 Найдите координаты ее вершин

10.3 Найдите значение ее параметра р

10.4 Запишите уравнение ее симметрии

10.5 Постройте данную параболу.

Решение:

B=9x²+24xy+16y²

λ₁=0, λ₂=25

Так как одно из собственных чисел равно нулю, то кривая – параболического типа.

Найдем собственные векторы. Для λ₁=0

3ξ = 4ξ₂

Положим ξ₁=4, ξ₂=4. Единичный с.в.

λ₂=25

4ξ = 3ξ₂

Положим ξ₁=3, ξ₂=4 Единичный с.в.

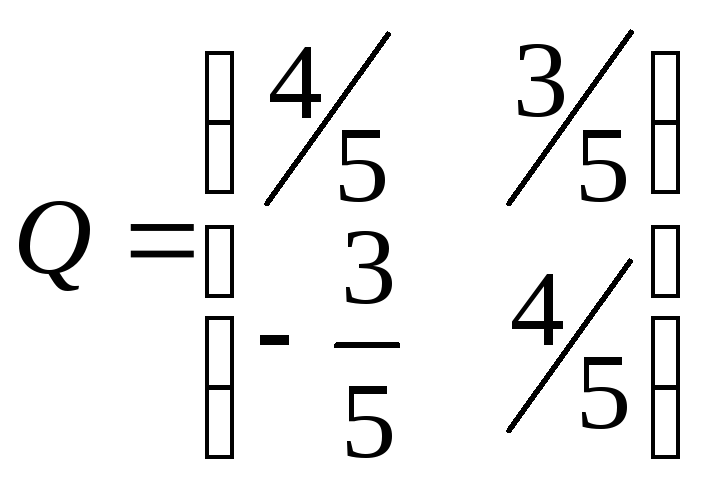
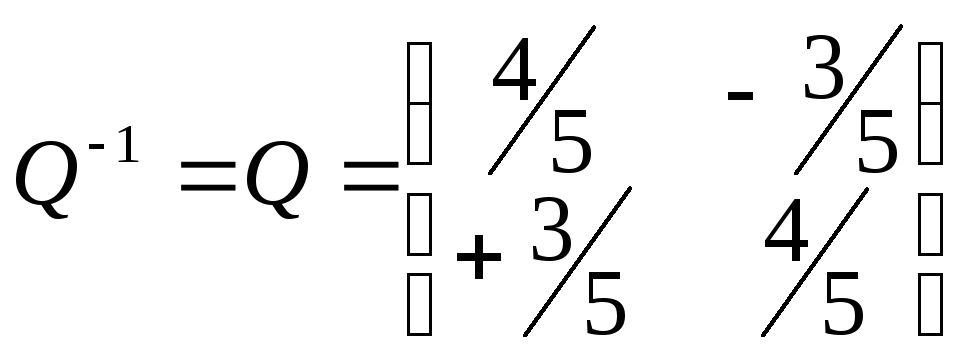
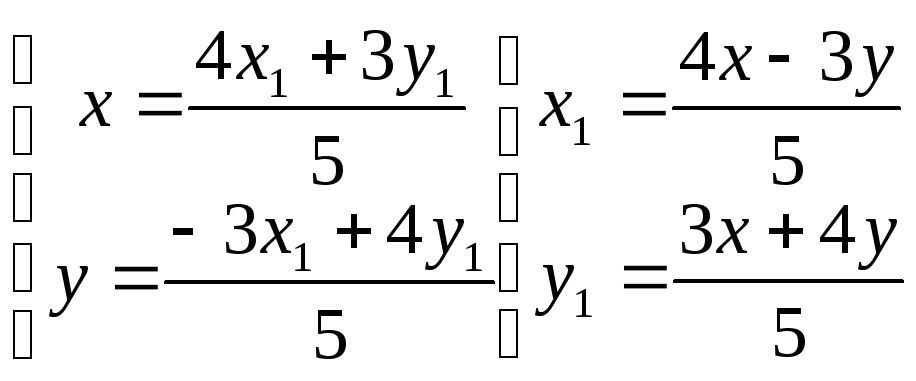
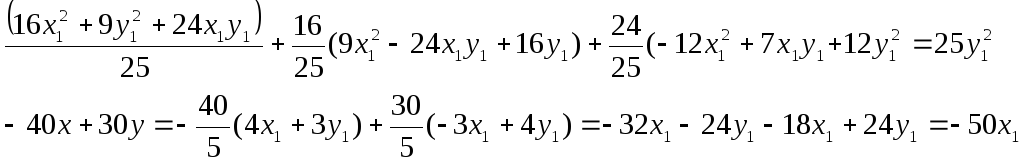
Уравнение параболы в новой системе координат:

Параметр параболы з=1 Осью симметрии является прямая y₂=0

Вершина параболы находится в точке 0(0;0)