1. Множество – это совокупность объектов (элементов), которые понимаются как единое целое.

Способы задания множеств:

• перечисление всех элементов множества (A = {a1, a2,…, an});

• предикат (разрешающая процедура) – это некоторое условие, выраженное в форме логического утверждения. Например, если для данного элемента выполняется какое-либо условие – принадлежит (A = {x | P(x)}, где P(x) – какое-то свойство).

• порождающая процедура, которая будучи запущенной, порождает некоторые элементы множества. Описывает способ получения элементов множества из уже полученных элементов либо других объектов. Тогда элементы множества - все объекты, которые могут быть получены (построены) с помощью такой процедуры (A = {x | x = f() } ).

• графический (диаграммы Эйлера-Венна (Венна)).

Операции над множествами:

• Пересечением множеств  и  называется множество , каждый элемент которого принадлежит и множеству , и множеству .

• Объединением множеств  и  называется множество , каждый элемент которого принадлежит множеству  или множеству .

• Разностью множеств  и  называют множество , каждый элемент которого принадлежит множеству  и не принадлежит множеству .

• Симметрическая разность двух множеств — множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам.

• Дополнение - множество всех элементов, не принадлежащих A, т.е. множество U\A, где U – универсальное множество.

• Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают АхВ. Таким образом  АхВ = {(x;y) | x Є A, y Є B}.

К унарным операциям можно отнести абсолютное дополнение, мощность, булеан.

2. Разбиения и покрытия

Пусть U — универсальное множество, а I - произвольное множество и каждому элементу i∈I взаимно однозначно сопоставлено подмножество A_i⊆U.

Тогда говорят, что задано (индексированное) семейство множеств (A_i)_i∈I. Множество I называют множеством индексов, а множества A_i — элементами семейства (A_i)_i∈I.

В случае I∈N получаем последовательность множеств, или счетное семейство множеств;

если множество I конечно, получаем конечное семейство множеств. Таким образом, семейство (Ai)i∈I определено, если задано отображение ν:I→2^U.

Отметим, что любое множество, элементы которого есть некоторые подмножества универсального множества U, т.е. любое множество A⊆2^U, можно считать семейством (Ai)i∈I, где I=A, a ν — тождественное отображение множества A на себя.

Разбиение M – семейство множеств, которые являются подмножествами M и попарно не пересекаются. ( и  при  )

Покрытие М – семейство множеств, которые являются подмножествами М и могут пересекатся между собой.

Семейство называется дизъюнктным, если состоит из попарно не пересекающихся множеств, которые являются подмножествами А, но объединение этих множеств не даёт А.

Дизъюнктное покрытие – это разбиение.

3. Булеан – множество всех подмножеств множества A, обозначается P(A). Мощность конечного множества равна количеству ее элементов обозначается |A|. Мощность пустого множества равна 0. Если |A| = n, то |P(A)| = 2^n.

4. Свойства операций над множествами:

5. Прямое произведение А и В (обозначается AхВ) – это множество всех упорядоченных пар элементов (a, b), где a є A, b є В. При этом считается, что (a1, b1) = (a2, b2) тогда и только тогда, когда a1 = a2, b1 = b2.

Мощность прямого произведения равна |AхВ|=|A|*|B|.

Также рассматривают не только упорядоченные пары, но и наборы из нескольких элементов, которые называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем три элемента.

Декартовым произведением множеств А, А,…, A называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А, вторая – А, …, n-ая – множеству А: АА…A.

6. Бинарное отношение из множества A в множество B  любое подмножество 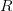 множества , то есть  (R отношение из A в B)

Способы задания БО: перечислением, таблицей, графом, графиком.

Область определения  БО  ρ  — множество, состоящее из таких x, для которых  〈x,y〉∈ ρ хотя бы для одного y.  D(ρ) ={x∃y |〈x,y〉 ∈ ρ}

Область значений БО ρ — множество, состоящее из таких y, для которых 〈x,y〉∈ ρ хотя бы для одного x.  R(ρ) ={y∃x |〈x,y〉∈ρ}

Инверсия (обратное отношение) ρ — называется множество упорядоченных пар , таких, что .

7. Произведение отношений. Степень отношений. Обобщенное понятие отношения.

Произведением отношений и называется отношение – совокупность пар , для которых существуют такие элементы , что , а .

Степенью отношения R на множестве называется его n-композиция (произведение) с самим собой.

Степень отношения определяется так:

Обобщенное понятие отношения – это подмножество прямого произведения множеств, то есть множество упорядоченных наборов (кортежей)