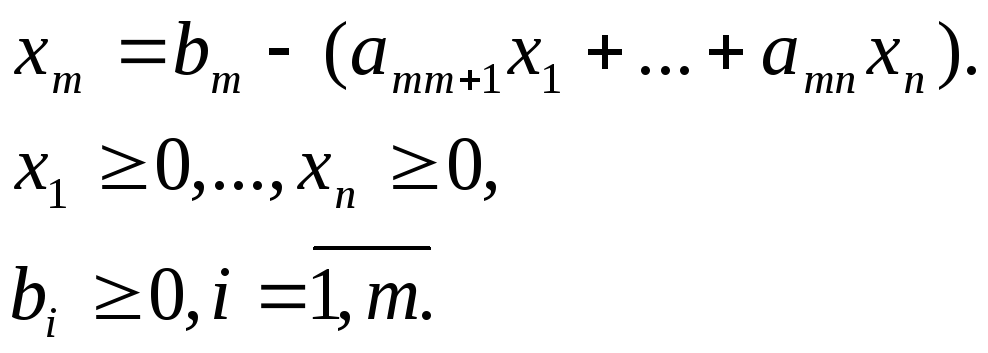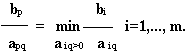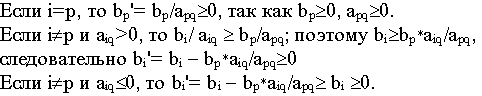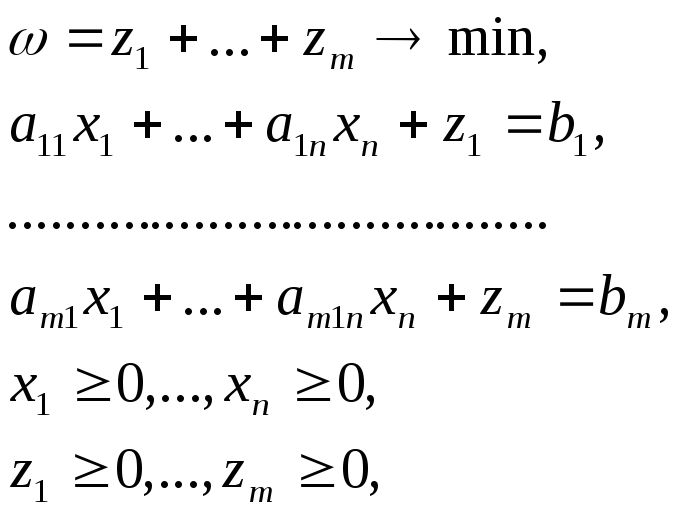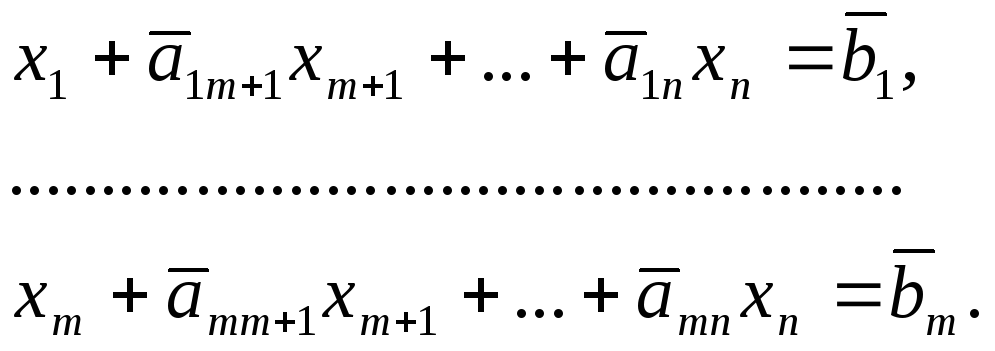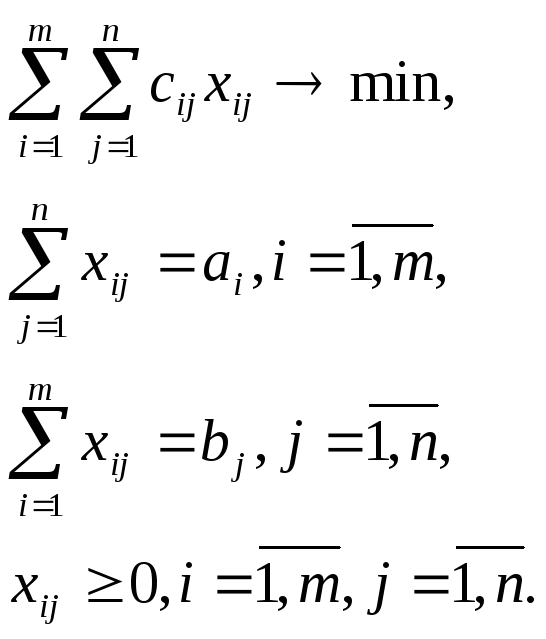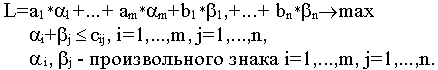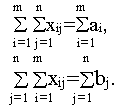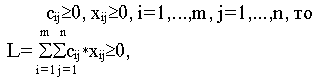Шпоры_метопт

1. Построение математической модели.

Для использования стандартных вычислительных алгоритмов ЛП требуется математическая запись модели. Таким образом, необходимо умение переводить словесное описание задачи на язык математических символов.

Составление математической модели начинают с выбора переменных, совокупность числовых значений которых однозначно определяет один из вариантов процесса. Следует иметь в виду, что иной раз от удачного выбора этих переменных зависит простота модели и, следовательно, удобство дальнейшего ее анализа.

После выбора переменных необходимо составить ограничения по тексту задачи, которым эти переменные должны удовлетворять. При этом нужно следить, чтобы в модель были включены все ограничительные условия, и в то же время не было ни одного лишнего или записанного в более жесткой, чем требуется условиями задачи, форме.

Наконец, составляется целевая функция, которая в математической форме отражает критерий выбора лучшего варианта.

После составления математической модели необходимо рассмотреть возможные пути ее упрощения и выбрать подходящий вычислительный метод для решения задачи.

2. Геометрическая интерпретация задач мат. программирования.

3. Классификация задач мат. программирования.

4. Графическое решение задач ЛП.

1. Графически могут решаться:

а) задачи, заданные в произвольной форме, содержащие не более двух переменных;

b) Задачи, заданные в канонической форме, с числом свободных переменных ;

c) Задачи в произвольной форме записи, которые после приведения к канонической форме будут содержать не более двух свободных переменных.

2. Основной формой для графического решения является 1-й тип задач. Поэтому, если встречается 2-й или 3-й тип задач, то предварительно их модель должна быть приведена к первому типу.

3. Решение задач 1-го типа выполняется в два этапа:

этап 1 -- построение области допустимых решений;

этап 2 -- построение в допустимой области оптимального решения.

4. При построении области допустимых решений может встретиться один из трех случаев:

а) пустая область – задача не имеет решения из-за несовместности системы ограничений в области допустимых решений;

б) выпуклый многоугольник – задача всегда имеет оптимальное решение;

в) неограниченная выпуклая многогранная область – в зависимости от направления вектора c (вектора коэффициентов целевой функции L) задача может иметь или не иметь решение.

5. Если оптимальное решение существует, то возможен один из трех исходов:

а) оптимальное решение единственное и совпадает с одной из вершин области;

б) оптимальные решения соответствуют всем точкам отрезка, соединяющего две вершины областии :

в) оптимальные решения соответствуют всем точкам допустимого луча, исходящего из вершины области :

5. Приведение произвольной задачи ЛП к канонической форме.

………………………

Каноническая форма (КФ) задачи характеризуется следующими тремя признаками:

1) однородная система ограничений в виде системы уравнений;

2) однородные условия неотрицательности, распространяющиеся на все переменные, участвующие в задаче;

3) минимизация (максимизация) целевой функции.

Известно, что для произвольной задачи ЛП можно построить эквивалентную ей каноническую задачу ЛП (эквивалентность двух задач означает, что оптимальному решению одной задачи соответствует оптимальное решение другой)[1,2,3].

6. Возможные формы решения задач ЛП геометрически.

7. Специальная форма задачи ЛП.

…………………………………………………

8. Определения, связанные с симплексной таблицей.

Одно из допустимых решений этой задачи можно найти, если переменные положить равными нулю. Такое решение называется допустимым базисным решением. Оно имеет вид:

Этому решению соответствует значение целевой функции . Переменные называют базисными, набор переменных называют базисом, а переменные называют небазисными или свободными. Число возможных базисов в задаче размерности n с m ограничениями не превосходит величину .

Среди элементов выбираем максимальный положительный элемент .Этот столбец объявляем ведущим (разрешающим).

Среди положительных элементов столбца находим элемент , для которого выполняется равенство:

Строку p объявляем ведущей (разрешающей). Элемент объявляем ведущим (разрешающим).

9. Правило перехода от одной симплексной таблицы к другой.

Составляем новую симплекс-таблицу, в которой:

а) вместо базисной переменной записываем , вместо небазисной переменной записываем ;

б) ведущий элемент заменяем на обратную величину ;

в) все элементы ведущего столбца (кроме ) умножаем на ;

г) все элементы ведущей строки (кроме ) умножаем на ;

д) оставшиеся элементы симплексной таблицы преобразуются по следующей схеме «прямоугольника».

Из элемента вычитается произведение трех сомножителей:

первый - соответствующий элемент ведущего столбца;

второй - соответствующий элемент ведущей строки;

третий - обратная величина ведущего элемента .

Преобразуемый элемент и соответствующие ему три сомножителя как раз и являются вершинами «прямоугольника».

10. Алгоритм симплекс метода для задачи на минимум в специальной форме.

Шаг 0 Подготовительный этап. Приводим задачу ЛП к специальной форме

Шаг 1 Составляем симплекс-таблицу, соответствующую специальной форме:

Шаг 2 Проверка на оптимальность.

Если среди элементов индексной строки симплекс – таблицы нет ни одного положительного элемента, то

оптимальное решение задачи ЛП найдено!

Шаг 3 Проверка на неразрешимость.

Если среди есть положительный элемент, а в соответствующем столбце - нет ни одного положительного элемента, то целевая функция L является неограниченной снизу на допустимом множестве. В этом случае оптимального решения не существует.

Шаг 4 Выбор ведущего столбца q.

Среди элементов выбираем максимальный положительный элемент.Этот столбец объявляем ведущим (разрешающим).

Шаг 5 Выбор ведущей строки p.

Среди положительных элементов столбца, находим элемент, для которого выполняется равенство:

Строку p объявляем ведущей (разрешающей). Элемент объявляем ведущим (разрешающим).

Шаг 6 Преобразование симплексной таблицы.

Шаг 7 Переход к следующей итерации - возврат к шагу 2.

11. Теорема о конечности алгоритма симплекс-метода.

  Для задачи ЛП симплекс-метод завершается через конечное число итераций.

Доказательство.

Каждой итерации симплекс-метода соответствует базисное допустимое решение задачи ЛП, переходу к новой итерации соответствует переход к новому базисному допустимому решению. Число базисных допустимых решений задачи ЛП конечно ( ). Если от итерации к итерации базисные допустимые решения не повторяются, то, перебрав в худшем случае все базисные допустимые решения, можно получить оптимальное решение или выяснить, что целевая функция неограничена, через конечное число итераций.

            Итак надо показать, что в невырожденном случае допустимые базисные решения не повторяются.

            Пусть х и х' - допустимые базисные решения для старой и новой симплекс-таблиц. Так как базисные решения невырождены, то 

            Поэтому 

т.е. значение целевой функции строго убывает при переходе старого решения х к новому допустимому базисному решению x' и  Следовательно, базисные допустимые решения не повторяются.

Доказано!

12. Критерий оптимальности симплекс-метода для задачи на минимум.

Если в индексной строке допустимой симплексной таблицы

то соответствующее допустимое базисное решение является оптимальным решением.

Доказательство.

На базисном решении

целевая функция имеет значение

Рассмотрим любое допустимое решение

Тогда

поскольку Для любого допустимого решения х' получили неравенство что означает оптимальность решения х. Доказано!

13. Критерий неограниченности симплекс-метода для задачи на минимум.

Пусть существует для которого столбец

Тогда целевая функция L неограничена сниузу на допустимом множестве.

Доказательство.

Рассмотрим для t>0 вектор

, где

Для любого t>0 вектор допустим, так как

и выполняются ограничения-равенства А =b. Но значение целевой функции

неограниченно убывает при так как

Значит L(x) не ограничена снизу на допустимом множестве.

Критерий доказан

14. Теорема об убывании целевой функции в симплекс методе для задачи на минимум.

15. Теорема о ключевом отношении в симплекс-методе.

Если переменная вводится в базис вместо переменной , для которой выполняется ключевое отношение

, то в новой симплексной таблице все   новая таблица является допустимой.

Доказательство.

Новой симплексной таблице с элементами

соответствует новое базисное решение

Докажем, что

i=1,...,m.

Теорема доказана

16. Алгоритм симплекс метода для задачи на максимум в специальной форме.

Алгоритм симплекс-метода для задачи на максимум отличается от алгоритма для задачи на минимум только знаками индексной строки коэффициентов в целевой функции , а именно:

Шаг 0 Подготовительный этап. Приводим задачу ЛП к специальной форме

Шаг 1 Составляем симплекс-таблицу, соответствующую специальной форме:

Шаг 2 Проверка на оптимальность.

Если среди элементов индексной строки симплекс – таблицы нет ни одного положительного элемента, то

оптимальное решение задачи ЛП найдено!

Шаг 3 Проверка на неразрешимость.

Если среди есть отрицательный элемент, а в соответствующем столбце - нет ни одного отрицательного элемента, то целевая функция L является неограниченной снизу на допустимом множестве. В этом случае оптимального решения не существует.

Шаг 4 Выбор ведущего столбца q.

Среди элементов выбираем максимальный положительный элемент. Этот столбец объявляем ведущим (разрешающим).

Шаг 5 Выбор ведущей строки p.

Среди положительных элементов столбца, находим элемент, для которого выполняется равенство:

Строку p объявляем ведущей (разрешающей). Элемент объявляем ведущим (разрешающим).

Шаг 6 Преобразование симплексной таблицы.

Шаг 7 Переход к следующей итерации - возврат к шагу 2.

17. Критерий оптимальности симплекс-метода для задачи на максимум.

Если в индексной строке допустимой симплексной таблицы

то соответствующее допустимое базисное решение является оптимальным решением.

Доказательство.

На базисном решении

целевая функция имеет значение

Рассмотрим любое допустимое решение

Тогда

поскольку

Для любого допустимого решения х' получили неравенство

что означает оптимальность решения х.

Доказано!

18. Критерий неограниченности симплекс-метода для задачи на максимум.

Пусть существует для которого столбец

Тогда целевая функция L неограничена сниузу на допустимом множестве.

Доказательство.

Рассмотрим для t>0 вектор

, где

Для любого t>0 вектор допустим, так как

и выполняются ограничения-равенства А =b. Но значение целевой функции

неограниченно убывает при так как

Значит L(x) не ограничена снизу на допустимом множестве.

Критерий доказан

19. Теорема о возрастании целевой функции в симплекс-методе для задачи на максимум.

20. Вспомогательная задача ЛП и её свойства.

Вспомогательной задачей ЛП (ВЗЛП) называется задача вида                       

Переменные вспомогательной задачи

образуют базис ВЗЛП и называются искусственными.

21. Алгоритм метода искусственного базиса.

Шаг 1. Приводим задачу ЛП к канонической форме

Шаг 2. В каждую i-ю строку ограничений (17) вводим искусственную неотрицательную переменную x_i и строим вспомогательную задачу ЛП вида:

Шаг 3. Для построенной вспомогательной задачи строим симплексную таблицу

Шаг 4. Если и все переменные являются небазисными, то m переменных из войдут в базис и система ограничений, соответствующих симплексной таблице, будет иметь вид:

Шаг 5. Если , но в базисе остались искусственные переменные , для которых (вырожденный случай), то проводим для каждой искусственной переменной из базиса следующее преобразование симплексной таблицы:

Выбираем ведущим столбцом столбец такой переменной , для которой элемент индексной строки , а элемент столбца .

В этом случае строка искусственной переменной будет ведущей и после стандартного преобразования симплексной таблицы (шаг 6 из прямого симплекс – метода) искусственная переменная выведется из базиса.

Шаг 6. Если , то допустимого решения в исходной задаче (17) не существует (не могут все искусственные переменные быть равными нулю в задаче (18), а значит система ограничений задачи (17) несовместна) – процесс решения исходной задачи (17) завершается.

22. Алгоритм двойственного симплекс-метода.

Шаг 0. Начинаем с симплексной таблицы

где .

Шаг 1. Проверка на оптимальность. Если , то решение - оптимальное.

Шаг 2. Выбор ведущей строки. Выбираем среди номеров i, для которых , номер k с максимальным по модулю значением

Строка k объявляется ведущей.

Шаг 3. Проверка на неразрешимость. Если в строке нет отрицательных элементов, то двойственная целевая функция не ограничена и, следовательно, прямая задача не имеет допустимых решений. Процесс решения завершается.

Шаг 4. Выбор ведущего столбца s. Выбираем среди отрицательных элементов строки элемент с номером s, для которого выполняется равенство

Столбец s объявляется ведущим, а элемент - ведущим элементом.

Шаг 5. Проводим стандартное преобразование симплексной таблицы (Шаг 6 из прямого симплекс-метода).

Шаг 6 Преобразование симплексной таблицы.

Шаг 7 Переход к следующей итерации - возврат к шагу 2.

23. Схема формирования двойственной задачи.

24. Теорема об основном неравенстве двойственности.

Для любых допустимых решений прямой задачи х и для любых допустимых решений двойственной задачи у выполняется неравенство  

Доказательство.

Из системы ограничений задачи 

Из системы ограничений задачи 

Объединяя полученные неравенства, имеем 

Теорема доказана.

25. Основная теорема двойственности и её следствия.

Первая теорема двойственности. Если одна из пары двойственных задач (I) и (II) разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают:

где – оптимальные планы задач (I) и (II) соответственно.

Говорят, что допустимые решения x,y удовлетворяют условиям дополняющей не жесткости (УДН), если при подстановке этих векторов в ограничения задач (I) и (II) хотя бы одно из любой пары сопряженных неравенств обращается в равенство.

Вторая теорема двойственности. оптимальны в задачах (I) и (II) тогда и только тогда, когда они удовлетворяют УДН.

26. Теорема о дополняющей не жесткости.

27. Следствие из теоремы о дополняющей не жесткости.

28. Проверка вектора на оптимальность с помощью УДН.

29. Решение пары двойственных задач с помощью УДН.

30. Экономическая интерпретация прямой задачи УДН.

31. Экономическая интерпретация двойственной задачи УДН.

32. Экономическая интерпретация теорем двойственности.

Рассмотрим экономическую интерпретацию основного неравенства двойственности. Так как

 - прибыль от реализации единицы продукции, а

 - количество произведенной j-й продукции, то

характеризует суммарную прибыль от реализации произведенной

продукции. Так как  - количество i-го ресурса, а

 - ценность единицы ресурса, то

характеризует суммарную ценность всех ресурсов. Тогда из соотношения

следует, что до тех пор, пока прибыль меньше суммарной ценности ресурсов, решение остается оптимальным. Как только

,то решения х* и у* пары двойственных задач становятся оптимальными.

            Большой практический интерес представляет экономическая интерпретация второй теоремы двойственности, а также ее следствия  о дополняющей нежесткости.

            1. Если суммарная оценка  i-го ресурса положительна

то этот ресурс в соответствии с оптимальным планом  х* используется полностью

            2. Если i-й ресурс используется не полностью

то его оптимальная оценка нулевая    и i-е ограничение несущественно.

            3. Если в соответствии с оптимальным планом х* j-я продукция производится

то это производство эффективно, так как цена единицы j-й продукции

равна затратам на ее производство в единицах

            4. Если производство j-й продукции убыточно (приведенные издержки ненулевые

то в соответствии с оптимальным планом эта продукция не производится

33. Постановка задачи целочисленного ЛП и идея метода Гомори.

Задача целочисленного программирования (ЦЛП) формулируется так же, как и задача ЛП, но включается дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение должны быть целыми неотрицательными числами:

Симплекс – метод не гарантирует целочисленности решения задачи (22), поэтому для отыскания оптимального целочисленного решения задачи ЦЛП требуются специальные методы. Один из таких методов, приводящий к целочисленному решению за конечное число шагов, предложен американским математиков Р. Гомори [1,2]. Идея метода следующая.

С помощью симплекс – метода решается задача ЛП без условия целочисленности. Если оптимальное решение получается нецелочисленным, то вводится дополнительное ограничение, которое, уменьшая многогранник допустимых решений (отсекая некоторую его часть), не исключает из него целочисленных точек. Если оптимальное решение задачи ЛП с дополнительным ограничением целочисленное, то вычисления заканчивают; если же оптимальное решение содержит хотя бы одну дробную компоненту, добавляют новое дополнительное ограничение.

Процесс присоединения дополнительных ограничений повторяют до тех пор, пока либо не будет найдено целочисленное оптимальное решение, либо показано, что задача не имеет целочисленных решений.

34. Алгоритм метода Гомори.

Шаг 1. Симплекс-методом находим оптимальное решение задачи, без учета условия целочисленности. Если задача не имеет решения, то неразрешима и исходная задача ЦЛП. В случае алгоритм завершает работу.

Шаг 2. Строим таблицу

Если элементы– целые, то оптимальное решение является целочисленным. В этом случае вычисления заканчиваем. Иначе, переходим к следующему шагу.

Шаг 3. Среди дробных компонент таблицы выбираем элемент с максимальной дробной частью и по строке i составляем дополнительное ограничение:

Здесь - целая часть числа (наибольшее целое число, не превышающее число ).

Шаг 4. Добавляем построенное ограничение к последней симплекс-таблице и, применяя двойственный симплекс-метод, находим оптимальное решение. Переходим к шагу 2.

35. Классическая транспортная задача. Содержательная постановка.

Классическая транспортная задача ЛП формулируется следующим образом. Имеется m пунктов производства (поставщиков) и n пунктов потребления (потребителей) однородного продукта.

Транспортная задача, в которой суммарные запасы и суммарные потребности совпадают, называется закрытой моделью; в противном случае – открытой. Открытая модель решается приведением к закрытой.

Математическая закрытая модель транспортной задачи имеет вид:

36. Приведение открытой модели транспортной задачи к закрытой модели.

Транспортная задача, в которой суммарные запасы и суммарные потребности совпадают, называется закрытой моделью; в противном случае – открытой. Открытая модель решается приведением к закрытой.

В случае, когда суммарные запасы превышают суммарные потребности, т.е. , вводится фиктивный n+1 потребитель, потребности которого .

В случае, когда суммарные потребности превышают суммарные запасы, т.е. , вводится фиктивный m+1 поставщик, запасы которого .

37. Двойственная задача для транспортной задачи.

Запишем транспортную задачу в матричном виде

Двойственная задача к транспортной задаче в матричном виде будет иметь вид

у- произвольного знака.

            Распишем двойственную задачу в скалярном виде. Обозначим компоненты вектора

или  в общем виде двойственная задача

            Двойственные переменные ai, i=1,...,m, bj, j=1,...,n, называются платежами, а

- псевдостоимость перевозок единицы груза из пункта i в пункт j, i=1,...,m, j=1,...,n.

38. Теорема о разрешимости транспортной задачи.

Базисное решение закрытой модели транспортной задачи содержит m+n-1 базисных компонент.

Доказательство.

Количество базисных компонент определяется число линейно-независимых ограничений задачи. В транспортной задаче не все m+n ограничений линейно-независимы.

            Действительно, сложив первые m ограничений и  следующие n ограничений задачи, получим

            Но в закрытой модели выполняется балансовое равенство

            поэтому получаем, что нетривиальная линейная комбинация строк ограничений (линейная комбинация с ненулевыми коэффициентами) равна нулю. Это означает, что среди ограничений задачи есть линейно-зависимое ограничение. Следовательно, число линейно-независимых ограничений равно  m+n-1 и базис задачи состоит из m+n-1 компонент.

Теорема доказана

39. Критерий оптимальности для транспортной задачи.

Оптимальный план закрытой модели транспортной задачи существует всегда.

Доказательство.

Оптимальное решение задачи ЛП существует, если, во-первых, существует допустимое решение и, во-вторых, целевая функция ограничена на этом допустимом решении.

            Покажем существование допустимого решения. Так как           

суммарные запасы 

совпадают с суммарными потребностями

то всегда можно найти такой план перевозок, который будет допустимым решением (все запасы вывозятся и все потребности выполняются в силу балансового равенства).

            Покажем ограниченность целевой функции.

            Так как

следовательно L ограничена снизу нулем для всех допустимых решений.

Теорема доказана

40. Метод северо-западного угла для нахождения начального опорного плана.

Рассмотрим «северо-западный угол» незаполненной таблицы, т.е. клетку, соответствующую первому поставщику и первому потребителю.

Возможны три случая:

1. Если , то . Это означает, что первый поставщик отгрузил весь продукт первому потребителю и его запас равен нулю, поэтому . При этом неудовлетворенный спрос в первом пункте потребления равен .

2. Если , то , т.е. спрос первого потребителя полностью удовлетворен и поэтому , а остаток продукта в первом пункте производства равен .

3. В случае из рассмотрения можно исключить и поставщика и потребителя. Однако при этом план получается вырожденным, поэтому считается, что выбывает только поставщик, а спрос потребителя остается неудовлетворенным и равным нулю.

После этого рассматриваем северо-западный угол оставшейся незаполненной части таблицы и повторяем те же действия. В результате через шагов получим опорный план.

41. Метод минимальной стоимости.

Отличается от метода северо-западного угла только тем, что вместо «северо-западного» угла незаполненной таблицы выбирается клетка с минимальной стоимостью.

Возможны три случая:

1. Если , то . Это означает, что первый поставщик отгрузил весь продукт первому потребителю и его запас равен нулю, поэтому . При этом неудовлетворенный спрос в первом пункте потребления равен .

2. Если , то , т.е. спрос первого потребителя полностью удовлетворен и поэтому , а остаток продукта в первом пункте производства равен .

3. В случае из рассмотрения можно исключить и поставщика и потребителя. Однако при этом план получается вырожденным, поэтому считается, что выбывает только поставщик, а спрос потребителя остается неудовлетворенным и равным нулю.

После этого рассматриваем северо-западный угол оставшейся незаполненной части таблицы и повторяем те же действия. В результате через шагов получим опорный план.

42. Метод потенциалов. Терминология, критерий оптимальности в содержательной интерпретации.

Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией, которая в каждой клетке цикла совершает поворот на . Знаком «+» отмечают те вершины, в которых перевозки увеличиваются, а знаком «-« - те вершины цикла, в которых перевозки уменьшаются. Перемещение какого-то количества единиц груза по циклу означает увеличение перевозок на это количество единиц в положительных вершинах и уменьшение в отрицательных вершинах. При этом, если перевозки остаются неотрицательными, план остается допустимым, а стоимость плана может меняться.

Ценой цикла называется изменение стоимости перевозок при перемещении единицы груза по этому циклу. Очевидно, цена цикла равна алгебраической сумме стоимостей, стоящих в вершинах цикла, при этом стоимости в положительных вершинах берутся со знаком «+», а в отрицательных со знаком «-«.

Идея метода потенциалов состоит в следующем [1,3]. Для любой свободной клетки транспортной таблицы всегда существует единственный цикл, положительная вершина которого лежит в этой свободной клетке, а все остальные в базисных. Если цена такого цикла отрицательна, то план можно улучшить перемещением перевозок по данному циклу. Количество единиц груза, которое можно переместить определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить больше единиц груза, возникнут отрицательные перевозки). Если циклов с отрицательной ценой нет, то это означает, что дальнейшее улучшение плана невозможно, т.е. оптимальный план найден.

43. Алгоритм метода потенциалов.

Шаг 1. Строим опорный план (методом северо-западного угла или методом минимальной стоимости) с базисными клетками.

Шаг 2. Определяем платежи , из условий: для всех базисных клеток (ij). Один из платежей (в строке или столбце которого максимальное число базисных клеток) полагаем равным нулю.

Шаг 3. Считаем псевдостоимости для всех свободных клеток. Если для всех клеток, то план оптимален. Вычисляем значение целевой функции на этом плане и исследование прекращаем.

Шаг 4. Если есть свободная клетка, для которой , то улучшаем план, перебрасывая перевозки по циклу этой свободной клетки.

Шаг 5. Возвращаемся к шагу 2 для пересчета платежей нового опорного плана.

44. Транспортная задача по критерию времени. Содержательная постановка.

45. Метод запрещенных клеток.