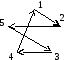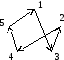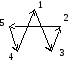ВАРИАНТ 6

Министерство образования и науки Российской Федерации

ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (ОмГТУ)

Кафедра «Автоматизированные системы обработки информации и управления»

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

по дисциплине «Дискретная математика»

ВАРИАНТ 6

Принял:

преподаватель М.В. Девятерикова

подпись, дата

Выполнила:

студентка гр. АС-123 В.Е. Кузнецова

подпись, дата

Омск 2004

Задание 1. Для неориентированного графа, заданного матрицей расстояний, найти:

а) все гамильтоновы контуры;

б) кратчайший гамильтонов контур.

-	7	1	6	4
	-	5	1	3
		-	2	8
			-	1
				-

Таблица 1 – Матрица расстояний

Теория: Гамильтонов контур – такой контур, по которому можно обойти все вершины графа по одному разу и вернуться в исходную.

Решение:

Гамильтоновы контуры.

123451 (рисунок 1.1)

M = 7+5+2+1+4=19 – суммарный вес контура

123541 (рисунок 1.2)

M = 7+5+8+1+6=27

124351 (рисунок 1.3)

M = 7+1+2+8+4=22

124531 (рисунок 1.4)

M = 7+1+1+8+1=18

125341 (рисунок 1.5)

M = 7+3+8+2+6=26

125431 (рисунок 1.6)

M = 7+3+1+2+1=14

132451 (рисунок 1.7)

M = 1+5+1+1+4=12

132541 (рисунок 1.8)

M = 1+5+3+1+6=16

142351 (рисунок 1.9)

M = 6+1+5+8+4=24

142531 (рисунок 1.10)

M = 6+1+3+8+1=19

143251 (рисунок 1.11)

M = 6+2+5+3+4=20

152431 (рисунок 1.12)

M = 4+3+1+2+1=11

Рисунок 1. 1 Рисунок 1. 2 Рисунок 1. 3 Рисунок 1. 4

Рисунок 1. 5 Рисунок 1. 6 Рисунок 1.7 Рисунок 1.8

Рисунок 1..9 Рисунок 1.10 Рисунок 1.11 Рисунок 1.12

Кратчайший гамильтонов контур.

Из множества M={19,27,22,18,26,14,12,16,24,19,20,11}, содержащего суммарные веса контуров, выберем наименьшее.

min{19,27,22,18,26,14,12,16,24,19,20,11} = 11.

Это суммарный вес контура 152431 (рисунок 1.12)

Задание 2. Для неориентированного графа, заданного матрицей расстояний, найти:

1) дерево кратчайших путей;

2) остов минимальной длины;

3) максимальное независимое множество;

4) раскраску графа, используя алгоритмы 1 и 2 раскраски, алгоритм точной раскраски.

-	1	-	-	1	-	5	3	1	2
	-	4	-	-	7	6	-	1	-
		-	3	2	-	5	-	1	-
			-	4	1	-	-	2	1
				-	-	5	-	1	1
					-	-	-	2	5
						-	4	2	-
							-	7	-
								-	1
									-

Таблица 2 – Матрица расстояний

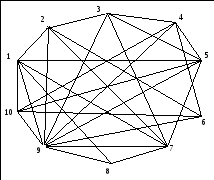
Рисунок 2 – Исходный граф

1) Дерево кратчайших путей;

Теория: Дерево – связанный граф, не имеющий циклов.

Алгоритм Дейкстры:

W={S},  - массив расстояний до S, S – корень дерева.

Цикл по вершинам (по i)

V*: (V*) = min (V_i);

W: =W+ {V*};

V_j not in W: (V_j):=min {(V_j), (V*) +S_ij}.

Решение:

Для нахождения дерева кратчайших путей используем алгоритм Дейкстры.

W = {1} – начальная вершина.

Найдем расстояния от начальной вершины до всех остальных.

(2) = 1, (3) = , (4) = , (5) = 1, (6) = , (7) = 5, (8) = 3, (9) = 1, (10) = 2.

(2)=(5)=(9)=min (V)

V*=2; W={1,2}

(3)=1+4=5, (6)=1+7=8.

(5)=(9)=min (V)

V*=5; W={1,2,5}

(4)=5.

(9)=min (V)

V*=9; W={1,2,5,9}

(3)=2, (4)=3, (7)=3.

(3)=(10)=min (V)

V*=3; W={1,2,5,9,3}

(10)=min (V)

V*=10; W={1,2,5,9,3,10}

(4)=(7)=(8)=min (V)

V*=4; W={1,2,5,9,3,10,4}

(6)=4.

(7)=(8)=min (V)

V*=7; W={1,2,5,9,3,10,4,7}

(8)=min (V)

V*=8; W={1,2,5,9,3,10,4,7,8}

(6)=min (V)

V*=6; W={1,2,5,9,3,10,4,7,8,6}

V-W=0.

Дерево кратчайших путей получено:

Рисунок 3 – Дерево кратчайших расстояний

2) Остов минимальной длины.

Теория: Задача о минимальном остовом дереве (МОД) заключается в нахождение остового дерева наименьшего суммарного веса.

Решение:

Используем алгоритм Прима. Начнем с первой вершины.

E={0}

min (E+V*)=12=15=19; E*=12; E=E+E*={12}

min (E+V*)=15=19=29; E*=15; E={12,15}

min (E+V*)=19=29=59=510; E*=19; E={12,15,19}

min (E+V*)=510=910; E*=510; E={12,15,19,510}

min (E+V*)=104=93; E*=104; E={12,15,19,510,104}

min (E+V*)=46=93; E*=46; E={12,15,19,510,104,46}

min (E+V*)=93; E*=93; E={12,15,19,510,104,46,93}

min (E+V*)=97; E*=97; E={12,15,19,510,104,46,93,97}

min (E+V*)=18; E*=18; E={12,15,19,510,104,46,93,97,18}

Все вершины включены в остов, следовательно остов минимальной длины получен. Его суммарный вес min=1+1+1+1+1+1+1+2+3=12.

Рисунок 4 – Остов минимальной длины

3) Максимальное независимое множество;

Множество вершин называется независимым, если никакие 2 вершины не смежные.

1) S = {1}, T = {3, 4, 6},

BT = ({1}, {3, 4, 6});

1.a) S = {1, 3}, T = {6},

BT = ({1, 3}, {6});

S₁ = {1, 3, 6}.

m = 3.

1.b) S₂ = {1, 4}.

m = 2.

2) S = {2}, T = {4, 5, 8, 10},

BT = ({2}, {4, 5, 8, 10});

2.a) S = {2, 4}, T = {8},

BT = ({2, 4}, {8});

S₃ = {2, 4, 8}.

m = 3.

2.b) S = {2, 5}, T = {8},

BT = ({2, 5}, {8});

S₄ = {2, 5, 8}.

m = 3.

2.d) S = {2, 10}, T = {8},

BT = ({2, 10}, {8});

S₅ = {2, 10, 8}.

m = 3.

Решая дальше, получим следующие независимые множества:

S₆ = {3, 8, 10}, m = 3;

S₇ = {3, 6, 8}, m = 3;

S₈ = {4, 7}, m = 2;

S₉ = {5, 6, 8}, m = 3;

S₁₀ = {6, 7}, m = 2;

S₁₁ = {7, 10}, m = 2;

S₁₂ = {8, 10}, m = 2;

S₁₃ = {9}, m = 1.

Максимальным независимым множеством являются множества S₁, S₃, S₄, S₅, S₆, S₇, S₉.

4) «Покраска» графа.

X(G) – хроматическое число – наименьшее число цветов, в которое можно раскрасить вершины графа так, чтобы любые смежные вершины имели разный цвет.

а) Алгоритм последовательного раскрашивания.

A={1, 2, 3, 4, 5, 6, 7, 8, 9, 10},

C(1)=1, C(2)=2, C(3)=1, C(4)=2, C(5)=3, C(6)=1, C(7)=4, C(8)=2, C(9)=5, C(10)=4.

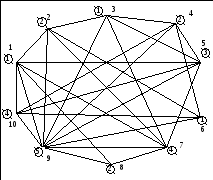
Рисунок 5 – Приблизительная раскраска графа по алгоритму последовательного раскрашивания

б) Улучшенный алгоритм последовательного раскрашивания.

Запишем степени каждой вершины:

∆(1)=6, ∆(2)=5, ∆(3)=5, ∆(4)=5, ∆(5)=6, ∆(6)=4, ∆(7)=6, ∆(8)=3, ∆(9)=9, ∆(10)=5.

Теперь упорядочим их по неубыванию: 9, 1, 5, 7, 2, 3, 4, 10, 6, 8 и пронумеруем заново (Рисунок 6).

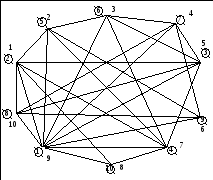
Рисунок 6 – Нумерация вершин графа для улучшенного алгоритма раскрашивания

Теперь цикл пойдет по вершинам в соответствии с их новыми номерами:

C(9)=1;

C(1)=2, C(3)=2, C(6)=2;

C(5)=3, C(2)=3, C(8)=3;

C(7)=4, C(4)=4;

C(10)=5.

Граф раскрашен. Как и в предыдущем случае, раскраска приблизительная (Рисунок 7).

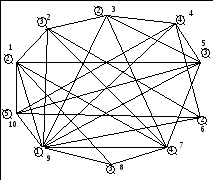
Рисунок 7 – Приблизительная раскраска графа по улучшенному алгоритму раскраски

в) Алгоритм точной раскраски.

Теория: Алгоритм основан на нахождении максимального независимого множества.

а) Находим максимальное независимое множество S графа G.

б) Красим S в цвет 1.

в) G: =G-S

Затем вновь идет шаг а и так до тех пор, пока в G есть хотя бы одна вершина.

Решение:

Шаг 1. Покрасим вершины, полученного в пункте 2.3 максимального независимого множества S₁= {1, 3, 6}, в цвет 1 (рисунок 8).

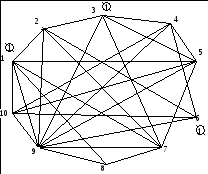
Рисунок 8 – Раскраска графа, шаг 1

Шаг 2. Найдем максимальное независимое множество среди вершин, не вошедших в множество S₁.

W = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – множество всех вершин графа.

W₁ = {2, 4, 5, 7, 8, 9, 10} - множество вершин графа, не вошедших в множество S₁.

Решая аналогично пункту 2.3 получим следующие независимые множества:

S₁₄ = {1, 4}, m = 2;

S₁₅ = {2, 4, 8}, m = 3;

S₁₆ = {2, 5, 8}, m = 3;

S₁₇ = {2, 8, 10}, m = 3;

S₁₈ = {4, 7}, m = 2;

S₁₉ = {5, 8}, m = 2;

S₂₀ = {7, 10}, m = 2;

S₂₁ = {9}, m = 1.

Максимальные независимые множества: S₁₅, S₁₆, S₁₇. Покрасим вершины множества S₁₅ = {4, 2, 8} в цвет 2 (рисунок 9).

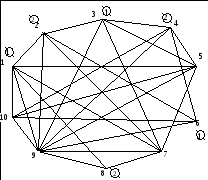
Рисунок 9 – Раскраска графа, шаг 2

Шаг 3. Найдем максимальное независимое множество среди вершин, не вошедших в множества S₁ и S₁₅.

W₂ = {5, 7, 9, 10} - множество вершин графа, не вошедших в множества S₁ и S₂.

Решая аналогично пункту 2.3 получим следующие независимые множества:

S₂₂ = {5}, m = 1;

S₂₃ = {7, 10}, m = 2;

S₂₄ = {9}, m = 1;

Выберем из множества W₂ максимальное независимое множество S₂₃ = {7, 10} и раскрасим его вершины в цвет 3. Из оставшегося множества вершин W₃ = {9, 5} мы получим независимые множества {5}, {9} и раскрасим их соответственно в цвета 4 и 5. Данная раскраска (рисунок 10) является точной. X(G) = 5 – минимальное хроматическое число графа.

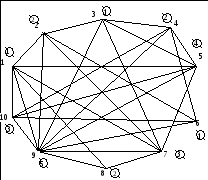
Рисунок 10 – Раскраска графа, результат

10