V. Методические указания по выполнению контрольной работы

ЗАДАЧА 1 (вариант …). Найти пределы функций, не пользуясь правилом Лопиталя в пунктах а) – г), с использованием правила Лопиталя в пункте д).

Решение. а)

Имеем неопределенность вида , так как пределы числителя и знаменателя равны нулю, т. е. . Следовательно, теорему о пределе частного здесь применить нельзя. Для раскрытия этой неопределенности разложим числитель и знаменатель на множители:

Таким образом,

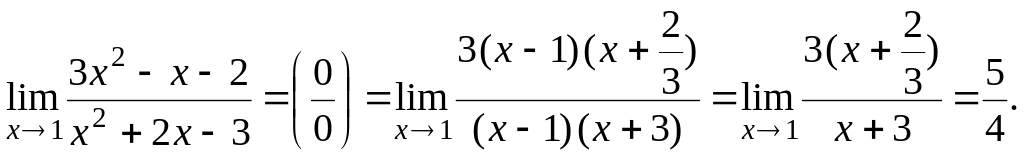
Ответ:

б)

Имеем неопределенность вида , так как пределы числителя и знаменателя равны нулю. Для раскрытия этой неопределенности умножим числитель и знаменатель дроби на выражение, сопряженное числителю, т. е. на . Таким образом,

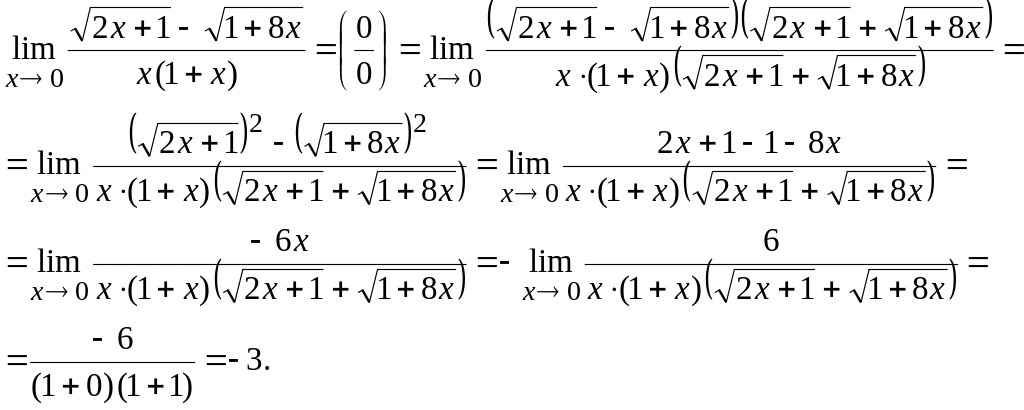
Ответ: -3.

в)

Имеем неопределенность вида 1^, так как

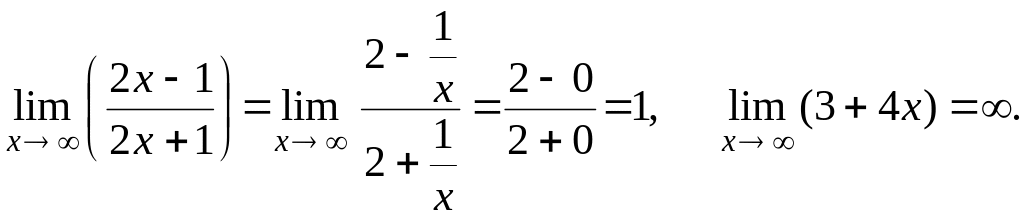
Преобразуем функцию так, чтобы использовать второй замечатель-

ный предел

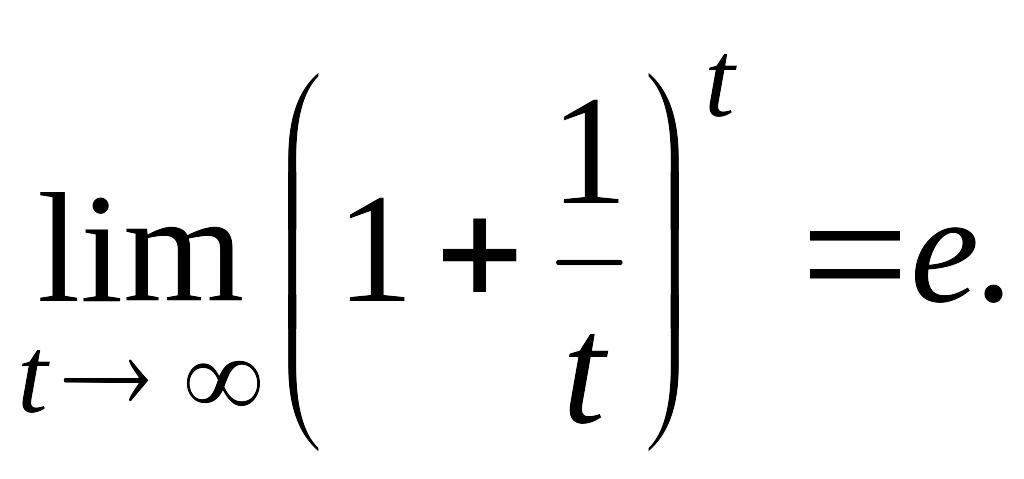
Таким образом,

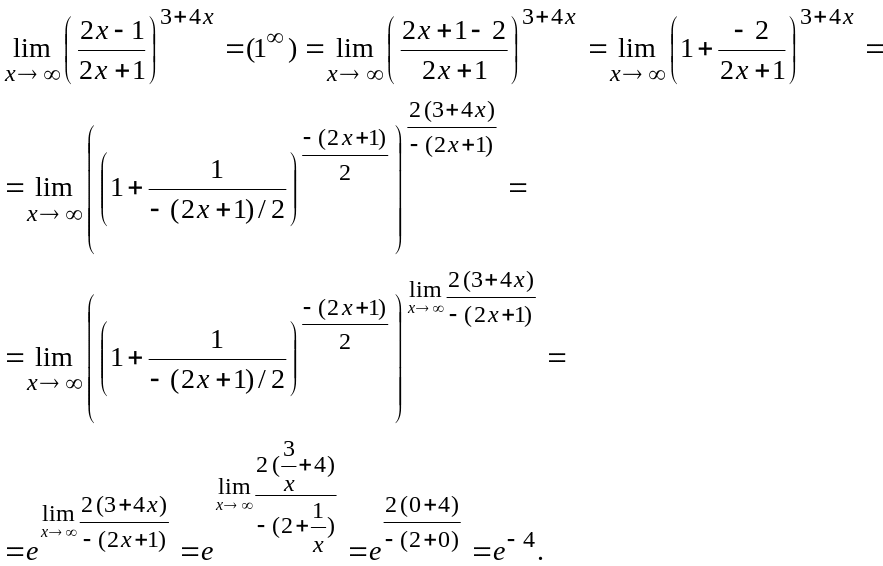
Ответ: .

г)

Имеем неопределенность вида . Для раскрытия этой неопределенности воспользуемся формулой и первым замечательным пределом

Таким образом,

Ответ: 2.

д)

Имеем неопределенность вида 0⁰. Для раскрытия этой неопределенности преобразуем исходную функцию, воспользовавшись равенством

Таким образом,

В показателе степени имеем неопределенность вида . Для раскрытия этой неопределенности воспользуемся правилом Лопиталя:

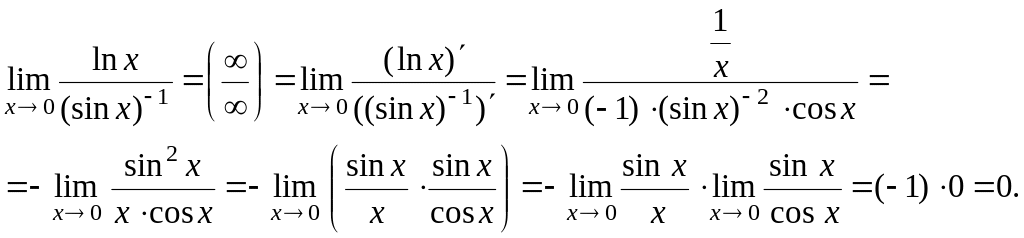
Окончательно имеем:

Ответ: 1.

ЗАДАЧА 2 (вариант…). Производственная функция Кобба-Дугласа выражает зависимость объема выпущенной продукции z от объема основных фондов x и затрат труда у (в стоимостном выражении).

Требуется:

1. Найти максимальный выпуск продукции при бюджетном ограничении

2. Вычислить предельную фондоотдачу и предельную производительность труда в точке максимального выпуска. Как изменится максимальный объем выпускаемой продукции при малых изменениях найденных объема основных фондов и затрат труда (без учета бюджетных ограничений).

Решение:

1. Для того чтобы найти максимальный выпуск продукции, необходимо решить задачу нахождения условного максимума функции двух переменных . При этом бюджетное ограничение будет являться уравнением связи.

Рассмотрим один из способов решения этой задачи. Из уравнения связи находим функцию у = 3,3 – х и подставим ее в функцию . Получим функцию одной переменной

В результате этого задача нахождения условного максимума свелась к задаче нахождения максимума функции одной переменной z (x). Для решения этой задачи найдем вначале критические точки функции z (x). Для этого вычисляем первую производную z (x) и решаем уравнение z (x)= 0.

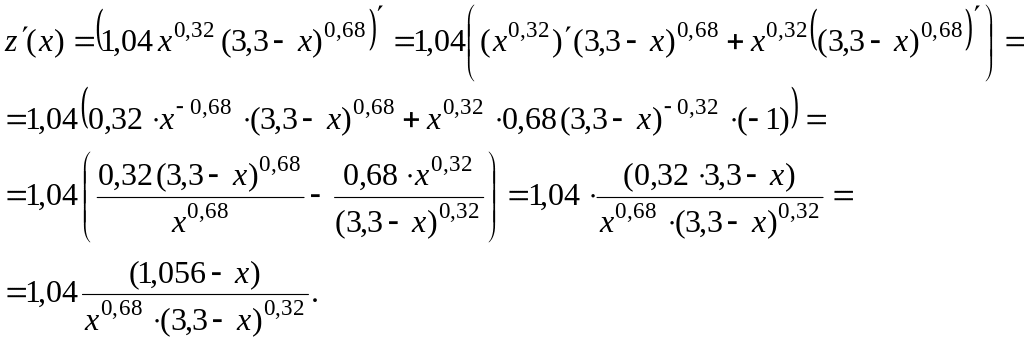
Решая уравнение z (x) = 0, находим критическую точку х₁ = 1,056. К критическим точкам функции z (x) относятся также и те точки из области определения, в которых первая производная z (x) не существует. В нашем случае к таким точкам относятся х₂ = 0, х₃ = 3,3. Значения функции z (x) в этих точках равны нулю, Так как решается задача нахождения максимума функции z (x), то эти точки не принимаем в рассмотрение.

Исследуем на экстремум функцию z (x) в критической точке х₁ = = 1,056, используя достаточный признак.

При переходе аргумента х слева направо через критическую точку х₁ производная z (x) меняет знак с “+” на “–”. Поэтому в точке х₁ функция z (x) имеет максимум.

Из уравнения связи находим Следовательно, функция в точке М имеет условный максимум

Ответ: Максимальный выпуск продукции .

2. Для производственной функции предельная фондоотдача есть частная производная , предельная производительность труда – .

Вычислим частные производные:

Вычислим значения частных производных в точке максимального выпуска, т. е. при х₁ = 1,056, у₁ = 2,244.

Изменение значения объема выпускаемой продукции при малых изменениях объема основных фондов и затрат труда приблизительно выражается полным дифференциалом

Подставляя найденные значения частных производных, получим

Ответ: предельная фондоотдача – 0,556;

предельная производительность труда – 0,555;

изменение объема выпускаемой продукции –

ЗАДАЧА 3 (вариант …). Производственная функция описывает зависимость производительности труда у от фондовооруженности (капиталовооруженности) х. Провести полное исследование функции и построить ее график. Выделить подмножества тех значений , при которых данная функция соответствует экономическому смыслу.

Решение.

1. Находим область определения функции.

Данная функция определена для всех значений х, за исключением значения х = 2, где знаменатель функции обращается в ноль. Следовательно, область определения является объединением двух бесконечных интервалов

2. Исследуем функцию на четность, нечетность, периодичность.

Так как D (y) не является симметричным множеством относительно начала координат, то данная функция не является четной, нечетной, периодической.

3. Исследуем функцию на экстремум. Находим интервалы возрастания и убывания.

Находим первую производную данной функции:

_.

Она определена для всех .

Находим критические точки функции. Для этого решаем уравнение

Получаем х = 3,6 – критическая точка.

Область определения функции разбиваем на три интервала: , , и определяем знак производной на каждом из них.

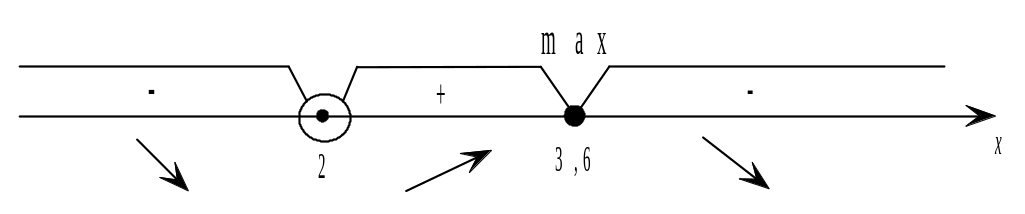
При , , следовательно, функция убывает на интервалах . При , , следовательно, функция возрастает на интервале (2; 3,6).

При переходе аргумента х через точку х = 2 (слева направо) производная меняет знак с “+” на “–”, следовательно, функция в точке х = 2 имеет локальный максимум. Значение функции в точке локального максимума .

4. Находим интервалы выпуклости, вогнутости и точки перегиба графика функции.

Найдем вторую производную данной функции:

Она определена для всех . Решая уравнение или , находим: х = 4,4 – критическая точка второго рода.

О бласть определения функции разбиваем на три интервала: и определяем знак производной на каждом из них.

При , , следовательно, график функции является выпуклым на интервалах .

При , следовательно, график функции является вогнутым на интервале

Так как при переходе аргумента через критическую точку х = 4,4 вторая производная меняет знак, то точка является точкой перегиба графика функции.

5. Находим предельные значения функции на концах интервалов области определения и асимптоты.

Следовательно, точка х = 2 является точкой разрыва второго рода, а прямая х = 2 – вертикальная асимптота графика функции.

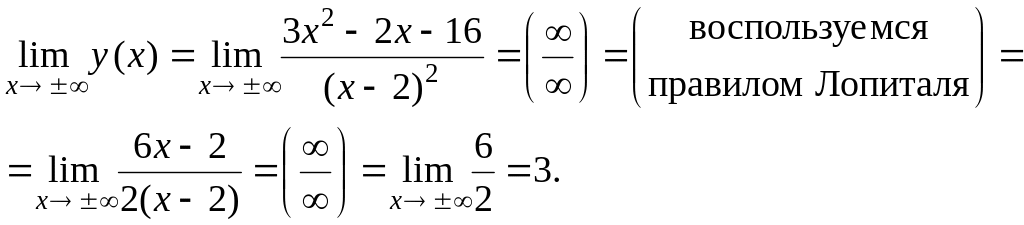
Найдем наклонные асимптоты .

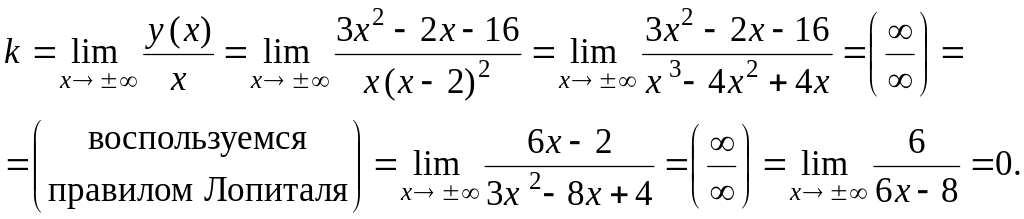
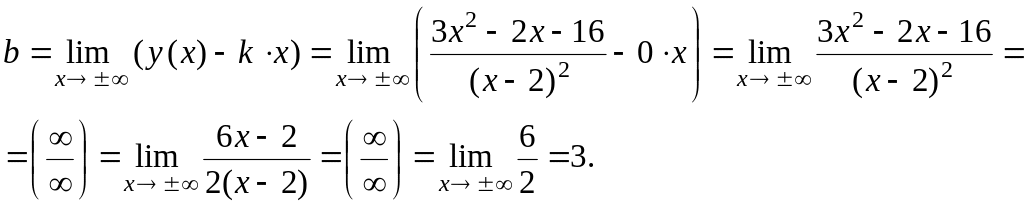
Следовательно, прямая или y = 3 является горизонтальной асимптотой.

6. Находим точки пересечения графика с осями координат.

При

При при

Следовательно, график данной функции пересекает координатные оси в точках

7. Результаты исследования занесем в таблицу.

x	(-; 2)	2	(2; 3,6)	3,6	(3,6; 4,4)	4,4	(4,4; +)
y	< 0		> 0	0	< 0	< 0	< 0
y	< 0		< 0	< 0	< 0	0	> 0
y	, 		, 	6,125 т. max	, 	5,78 т. перегиба	, 

8. По полученным данным строим график функции.

9. На интервале данная функция соответствует экономическому смыслу (с возрастанием фондовооруженности производительность труда возрастает).

ЗАДАЧА 4 (вариант …). Найти неопределенный интеграл. В пунктах а), б) результат интегрирования проверить дифференцированием.

Решение.

а)

Для вычисления данного интеграла применим формулу интегрирования по частям

где – дифференцируемые функции.

Таким образом,

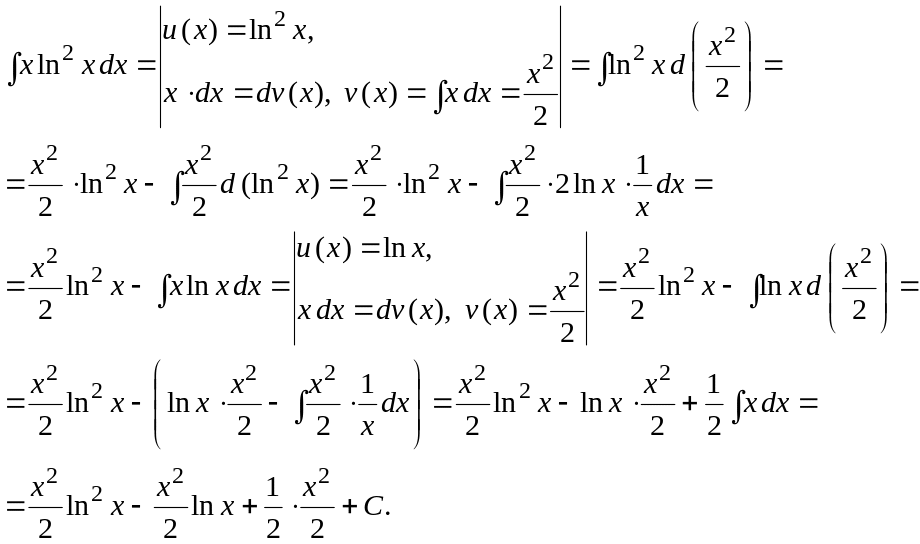
Результат проверим дифференцированием.

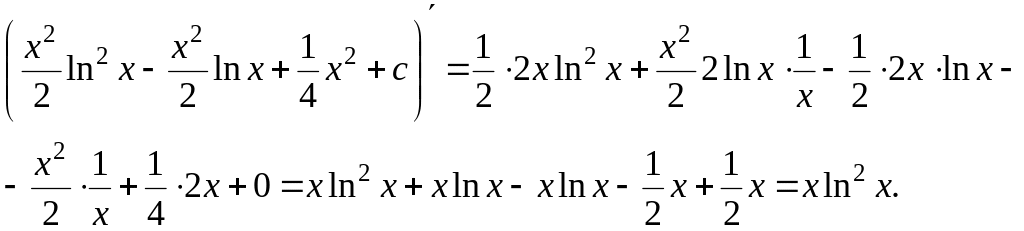
Ответ:

б)

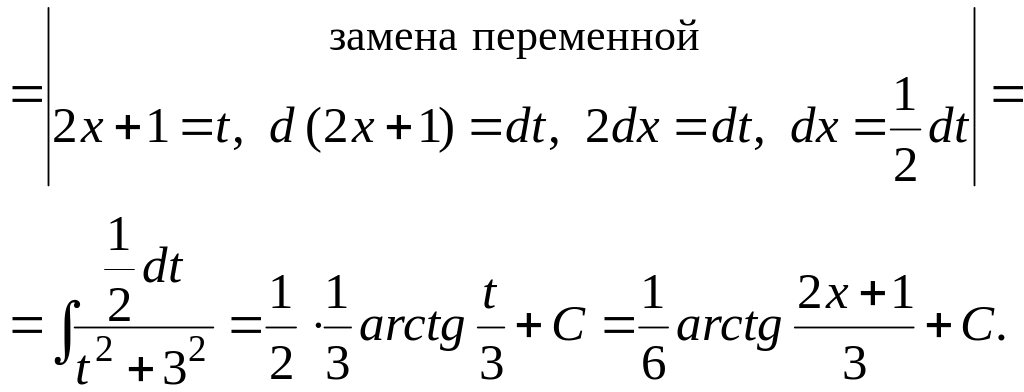
Результат проверим дифференцированием.

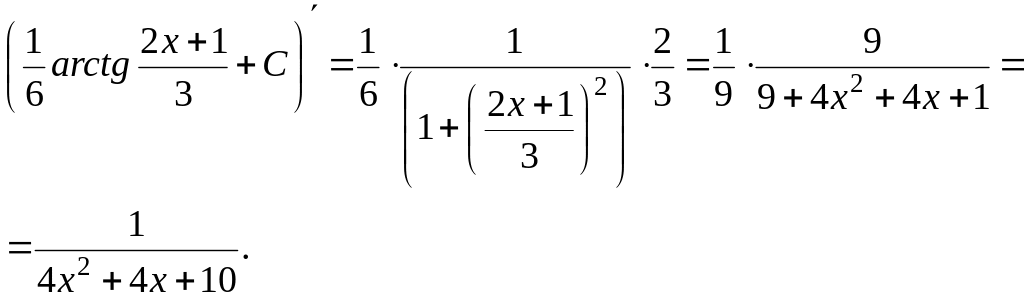
Ответ:

в)

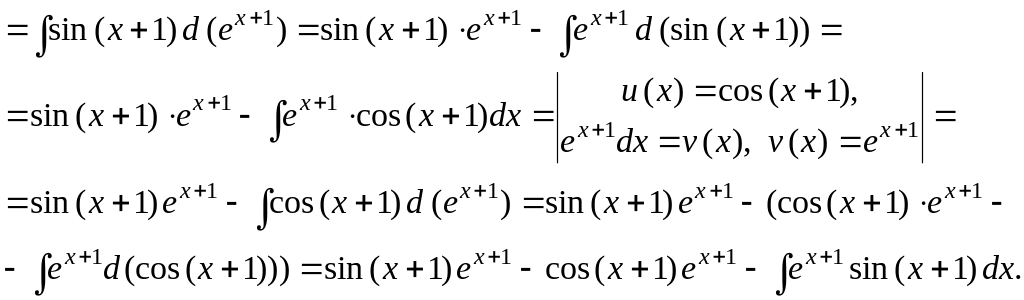
Таким образом получили соотношение относительно исходного интеграла

Решая полученное уравнение относительно I, получим

Ответ:

г)

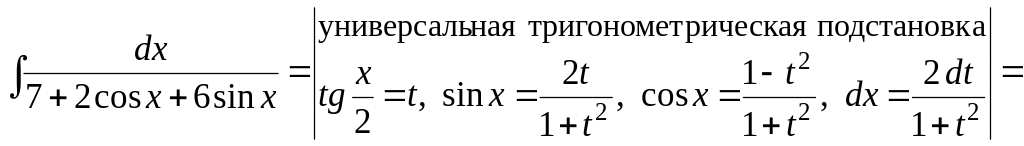
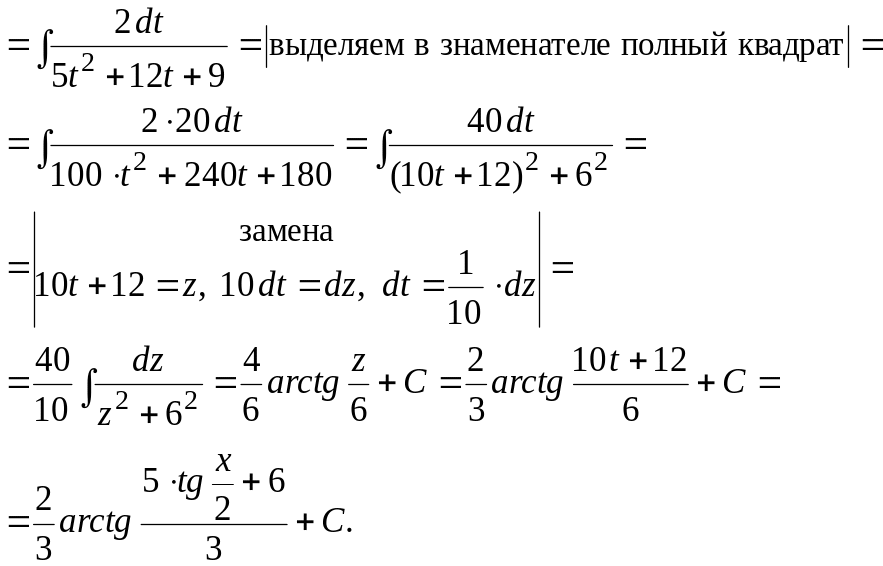
Ответ: .

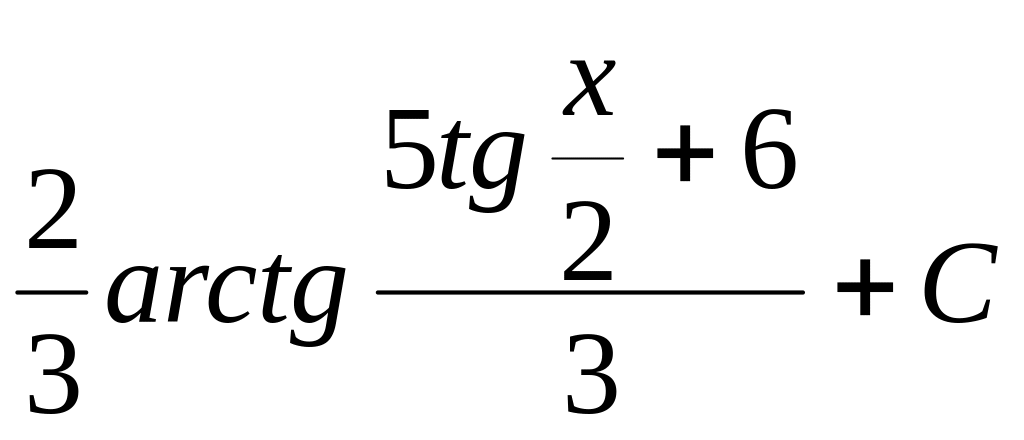ЗАДАЧА 5 (вариант…). Вычислить площадь фигуры (с точностью до 2-х знаков после запятой), ограниченной линиями

Решение.

Сделаем чертеж.

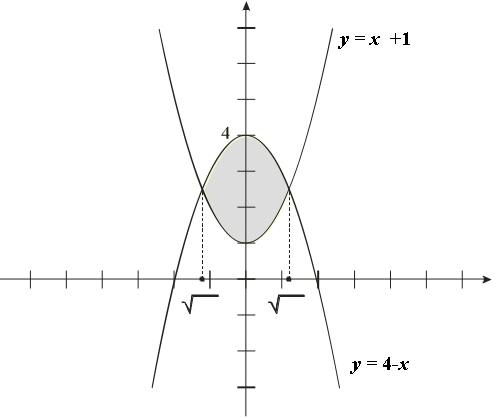
Найдем точки пересечения данных кривых. Для этого решаем систему уравнений:

Откуда

Площадь данной фигуры находим по формуле

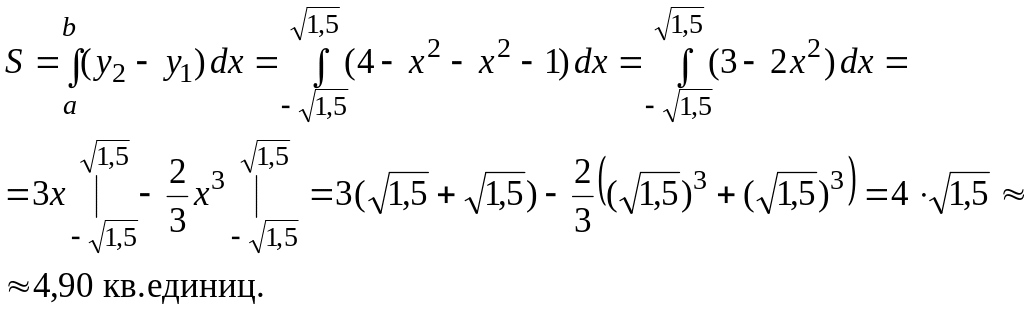
Ответ: 4,9 кв. единиц.

ЗАДАЧА 6 (вариант …). Найти частное решение линейного дифференциального уравнения первого порядка удовлетворяющего начальному условию

Решение.

Данное уравнение решаем с помощью подстановки где – неизвестные функции. Тогда Подставив в исходное уравнение, получим

. (*)

Найдем функцию v (x) из условия

Подставляем полученное выражение для v (x) в уравнение (*):

Тогда – общее решение исходного уравнения.

Из начального условия находим С:

Следовательно, – частное решение исходного уравнения.

Ответ:

ЗАДАЧА 7 (вариант…). Найти радиус сходимости, интервал сходимости и область сходимости степенного ряда

Решение.

Найдем радиус сходимости данного ряда по формуле

В нашем случае

Тогда

Следовательно, интервал сходимости данного ряда имеет вид

Исследуем сходимость ряда на концах интервала сходимости.

При степенной ряд превращается в числовой ряд

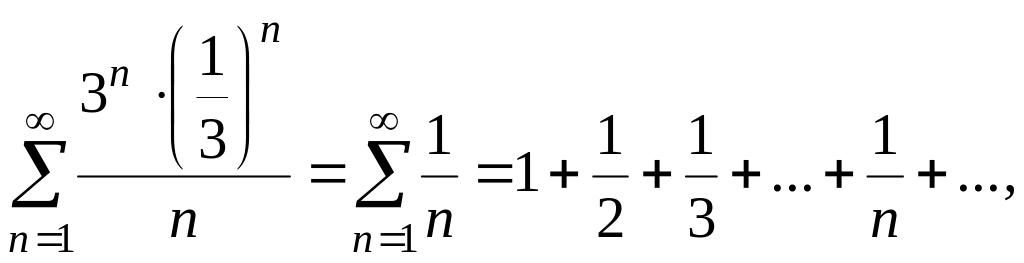
который расходится как гармонический ряд.

При степенной ряд превращается в числовой ряд

_{Error: Reference source not found}

.

Это – знакочередующийся ряд, члены которого убывают по абсолютной величине и Следовательно, по признаку Лейбница этот числовой ряд сходится.

Таким образом, промежуток – область сходимости данного степенного ряда.

Ответ: – радиус сходимости,

– интервал сходимости,

– область сходимости.

Приложение 1

Основные правила дифференцирования и таблица производных

Основные правила дифференцирования

Пусть с – постоянная, – функции, имеющие производные, тогда имеют место следующие формулы:

1)

2)

3)

4)

5)

6) Если т. е. где функции имеют производные, то – формула дифференцирования сложной функции.

Таблица производных основных элементарных функций

№	Вид функции	Производная	Сложная функция	Производная сложной функции
1.
2.
3.
4.
5.
Продолжение таблицы
№	Вид функции	Производная	Сложная функция	Производная сложной функции
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Приложение 2

Таблица основных неопределенных интегралов

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

Приложение 3

Институт бизнеса и менеджмента технологии БГУ

Кафедра менеджмента технологии