÷исельне ³нтегрування

функц³й одн³º¿ зм³нно¿

Чисельне ³нтегрування функц³й одн³º¿ зм³нно¿

(наближене обчислення означених ³нтеграл³в)

Нехай дана деяка функц³я f(x) на деякому в³др³зку [a,b]. Розглянемо задачу обчислення ¿¿ означеного ³нтеграла

.

ßêùî äëÿ f(x) â³äîìà ïåðâ³ñíà F(x) , то ³нтеграл обчислюºться за формулою Ньютона-Лейбн³ца

(1)

Однак F(x) для великого класу функц³й не можна виразити через елементарн³ функц³¿, тому означений ³нтеграл вже не можна обчислити за допомогою формули Ньютона - Лейбн³ца. Кр³м того, бувають випадки, коли п³д³нтегральна функц³я задаºться не анал³тично, а таблично. Тод³ використовують формули наближеного ³нтегрування, як³ називають квадратурними. Сам процес чисельного визначення ³нтегралу називають квадратурою, а в³дпов³дн³ формули - квадратурними.

²дея чисельних метод³в ³нтегрування полягаº в наступному. означений ³нтеграл

Ðèñ. 1

Ìàë. 1

можна трактувати як площу ф³гури (рис.1), обмежено¿ ординатами a ³ b , в³ссю абсцис x ³ граф³ком п³д³нтегрально¿ функц³¿ f(x) (кривол³н³йною трапец³ºю).

При наближеному обчисленн³ кривол³н³йну трапец³ю зам³няють ф³гурою, обмеженою тим самим в³др³зком [a;b] , площа яко¿ обчислюºться значно прост³ше.

Найб³льш прост³ формули чисельного ³нтегрування - формули прямокутник³в та трапец³й.

Ðèñ. 2

Розглянемо метод прямокутник³в.

³äð³çîê [a;b] розбивають на n â³äð³çê³â [x_i;x_i+1] , äå i= . На кожному з в³др³зк³в [x_i;x_i+1] площа кривол³н³йно¿ трапец³¿ зам³няºться площею прямокутника з основою [x_i;x_i+1] та висотою .

Òîä³ (2)

ßêùî â³äð³çêè [x_i;x_i+1] р³вновелик³ : h=x_i+1-x_i=

(3)

Формулу (3) називають також формулою «середн³х» прямокутник³в. Якщо за висоту прямокутника взяти f(x_i) àáî f(x_i+1), то можна одержати формули «л³вих» та, в³дпов³дно, «правих» прямокутник³в.

Формула л³вих прямокутник³в :

.

Формула правих прямокутник³в :

.

Похибка методу прямокутник³в

( гранична абсолютна похибка, похибка квадратурно¿ формули (3) ):

, (4)

äå , xÎ[a;b] .

Ðèñ. 3

Вираз (4) для похибки показуº, що формула (3) º точною для будь-яко¿ л³н³йно¿ функц³¿, оск³льки друга пох³дна тако¿ функц³¿ дор³внюº нулю, а отже похибка теж дор³внюº нулю.

Метод трапец³й

Ðèñ. 4

роз³б’ºм в³др³зок ³нтегрування [a;b] íà n р³вних частин, довжиною .

Дуга криво¿ f(x) зам³няºться стягуючою ¿¿ хордою. В точках розбиття проведемо ординати до перетину з кривою y=f(x). К³нц³ ординат з’ºднаºмо прямол³н³йними в³др³зками. Тод³ можна зам³нити кожну з одержаних кривол³н³йних трапец³й прямол³н³йною (рис.4). Площа кривол³н³йно¿ трапец³¿ ay₀y_nb можна вважати наближено дор³внюº сум³ площ прямол³н³йних трапец³й.

Площа л³во¿ трапец³¿

В³дпов³дно для трапец³¿, розм³щено¿ над д³лянкою (x_i-1,x_i) знайдемо:

(5)

Çâ³äñè

,

àáî (7)

Похибка методу

Гранична абсолютна похибка методу трапец³й знаходиться за формулою (8):

(8)

, , .

Сп³вставляючи формули (8) та (4) бачимо, що похибка формули середн³х прямокутник³в » в 2 рази менша, н³ж похибка формули трапец³й.

Програма, котра реал³зуº метод трапец³й з автоматичним вибором кроку

Метод С³мпсона

Цей метод значно точн³ший у пор³внянн³ з методами прямокутник³в або трапец³й.. Для досягнення то¿ ж точност³ в ньому можна брати менше число n д³лянок розбиття та в³дпов³дно б³льший крок h , а при одному й тому ж кроц³ h в³н даº менш³ абсолютну та в³дносну похибки.

Ðîç³á’ºì â³äð³çîê [a;b] на парне число 2n частин довжиною

(10)

Нехай точкам розбиття x₀=a ,x₁, x₂...x_2n=b в³дпов³дають значення п³д³нтегрально¿ функц³¿ y₀, y₁, y₂, ...y_2n ( тобто y_i=f(x_i), x_i=a+ih, i= )

Ðèñ. 5

Íà â³äð³çêó [x₀;x₂] проведемо через три точки (x₀,y₀), (x₁,y₁), (x₂,y₂) параболу, якою зам³нимо п³д³нтегральну функц³ю f(x).

Р³вняння параболи

y=Ax²+Bx+C (11)

(причому значення коеф³ц³ºнт³в À, Â, Ñ нев³дом³). Якщо зам³нити площу кривол³н³йно¿ трапец³¿ на в³др³зку [x₀;x₂] площею кривол³н³йно¿ трапец³¿, обмежено¿ параболою (11), то можна записати

(12)

Винесемо сп³льний множник (x₂-x₀)

(13)

Íåâ³äîì³ êîåô³ö³ºíòè À, Â, Ñ в р³вняннях (11), (13) шукаються з умови, що при

x={x₀, x₁, x₂}

f(x)={y₀, y₁, y₂}

Враховуючи, що x₁=(x₀+x₂)/2

(14)

Перемножуючи другу р³вн³сть (14) на 4 та додаючи вс³ три р³вност³, знайдемо

y₀+4y₁+y₂=A[x₀²+(x₀+x₂)²+x₂²]+B[x₀+2(x₀+x₂)+x₂]+6C=

=2A(x₀²+x₀x₂+x₂²)+3B(x₀+x₂)+6C , (15)

що сп³впадаº з квадратною дужкою р³вняння (13). Отже,

(16)

x₂-x₀=2h

Очевидно, що для кожно¿ наступно¿ пари д³лянок одержимо таку ж формулу:

(17)

Сумуючи р³вност³ вигляду (16) та (17)по вс³х в³др³зках, одержимо :

(18)

Це ³ º формула С³мпсона. Похибка методу (формули парабол) визначаºться за формулою :

, (19) , .

При написанн³ програм доц³льно формулу С³мпсона зобразити у вигляд³

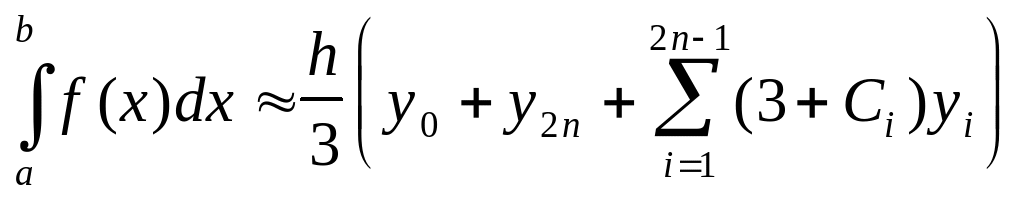, (20)

äå , тобто C_i=-C_i-1 ; C₁=1 ; i=

Програма, котра реал³зуº метод С³мпсона ³з сталим кроком ³нтегрування:

h=const, n2=20, C₁=1, .

Оц³нка похибки за правилом Рунге

Оц³нка похибки метод³в ³нтегрування за формулами (4), (8), (19) досить часто виявляºться малоефективною через труднощ³, пов’язан³ з оц³нкою пох³дних п³д³нтегрально¿ функц³¿ f(x) . Тому на практиц³ довол³ часто користуються прийомом, запропонованим Рунге. Нехай точне значення ³нтеграла , S_h - його наближене значення, обчислене за одн³ºю з квадратурних формул з кроком h , S_h/2 - наближене значення ³нтеграла, обчислене за тою ж формулою з кроком h/2.

Граничн³ значення абсолютних похибок можна записати у вигляд³ :

, (22) k - порядок точност³ формули ;

, (23) Ì - добуток стало¿ на пох³дну .

В³дпов³дно можна записати

I=S_h+D_h=S_h+h^kM=S_h/2+ ,

I=S_h/2+D_h/2=S_h/2+ .

В³дн³мемо ц³ р³вност³:

S_h/2-S_h=h^kM-M =M (2^k-1) .

Одержимо оц³нку похибки за правилом Рунге ( враховуючи (23)):

. (24)

Користуючись формулою (24), можна уточнити наближене значення ³нтеграла, вважаючи, що:

. (25)

Формулу (25) називають формулою екстраполяц³¿ за Р³чардсоном.

Оц³нка похибки за методом Рунге для формул прямокутник³в та трапец³й (к=2):

,

для формул С³мпсона (к=4):

.

Прийом багатократного зменшення кроку та оц³нки похибки (24) можна запрограмувати та одержати алгоритм автоматичного вибору кроку для наближеного обчислення ³нтеграла з заданою точн³стю.

Правило Рунге використовують, якщо задаºться гранична абсолютна похибка обчислення ³нтегралу.

Для одержання достатньо ефективно¿ програми (при оц³нц³ похибки за правилом Рунге) сл³д враховувати наступне. В формулах прямокутник³в, трапец³й ³ С³мпсона при подвоºнн³ числа крок³в нема необх³дност³ обчислювати значення п³д³нтегрально¿ функц³¿ знову в ус³х вузлах с³тки, оск³льки вузли с³тки, одержан³ при числ³ крок³в n , º вузлами с³тки ³ при числ³ крок³в 2n.

²Сторична дов³дка: Рунге.

Карл Давид Рунге (1856-1927) народився в Н³меччин³. В³н був четвертим, молодшим сином в заможн³й родин³ купц³в. Його батьки надавали перевагу англ³йськ³й мов³ ³ привчили сина до англ³йських погляд³в на життя. Вони прид³ляли особливу увагу спорту, виховуючи в хлопчику впевнен³сть в сво¿х силах ³ г³дн³сть. Молодий Рунге - високий, з чудовою ф³гурою, був до того ж винятковим ковзанярем. Все своº профес³йне життя в³н пров³в у Н³меччин³ - в Мюнхен³, Берл³н³, Гановер³ нарешт³, у Гетт³нген³. Близьким ³ гарячим другом Рунге протягом усього його життя був Макс Планк. Але усе ж Рунге вважав себе в ³нтелектуальному в³дношенн³ посл³довником Вейерштраса. Його рання робота з теор³¿ функц³й була виконана п³д кер³вництвом Леопольда Кронекера, але незабаром Рунге занурився в задач³ спектроскоп³¿ й астроф³зики, якими в основному ³ займався надал³. Майже ус³ його значн³ роботи в³дносилися до цих областей, але в³н н³коли не припиняв вважати себе математиком. Його ³нтереси поступово сфокусувалися на питаннях точност³, обробки ³ перетворення даних

Прикладна математика, як ¿¿ розум³в ³ застосовував Рунге, в³др³знялась в³д науки його сучасник³в. Його зовс³м не ц³кавило суворе математичне трактування моделей, виведених ³з ф³зичного досв³ду ³ дуже мало ц³кавили математичн³ методи, що у той час використовувалися в техн³ц³. В³н головним чином хот³в займатися теор³ºю ³ практикою чисельних метод³в, роблячи при цьому особливий наголос на практику. Деякими з його метод³в користуються ще ³ сьогодн³, особливо методом Рунге - Кутта для р³шення диференц³альних р³внянь. Проте математики не визнавали Рунге членом свого цеху; не визнавали його сво¿м ³ ф³зики. У результат³ в³н довго не одержував г³дно¿ ун³верситетсько¿ посади. У 1904 р. при ³нтенсивному сприянн³ з боку Планка ³ Фел³кса Клейна Рунге одержав м³сце професора в Гетт³нген³; це була перша (³ остання) професорська посада з прикладно¿ математики в Н³меччин³. У деякому сенс³ в³н був творцем ц³º¿ дисципл³ни й у т³ часи залишався в н³й ºдиним практикуючим викладачем. Не дивлячись на сво¿ л³беральн³ пол³тичн³ погляди п³д час першо¿ св³тово¿ в³йни, Рунге одержував все б³льше визнання серед колег по профес³¿, ³ в 1920 р. П³тер Дебай рекомендував його як свого спадкоºмця на зав³дування кафедрою, яку сам залишав, тому що Рунге був «ºдиною людиною в Гетт³нген³, спроможною керувати ф³зичним закладом».

Рунге в³д³йшов в³д справ у 1925 р., нав³ть не залишивши якогось талановитого студента, що побажав би вивчити його форму прикладно¿ математики, яку сьогодн³ ми назвали б чисельним анал³зом. В³н перебував у доброму здоров'¿ аж до своº¿ смерт³ в 1927 р. Рунге лишив двох син³в, чотирьох емансипованих дочок ³ залишився в с³мейн³й пам'ят³ д³дусем, що робив ст³йку на руках на святкуванн³ свого с³мдесятир³ччя.

Метод Гауса

Формулу Гауса називають формулою найвищо¿ алгебра¿чно¿ точност³, абсциси x_i при ³нтерполяц³¿ ( наближенн³, зам³н³ ) функц³¿ f(x) вибираються з умови забезпечення м³н³мально¿ похибки ³нтерполяц³¿. В метод³ Гауса ³нтеграл

(1)

зводиться до вигляду

, (2)

причому точне значення ³нтегралу зам³няºться на наближену квадратурну формулу.

Це зведення в³дбуваºться у наступн³й посл³довност³. У формул³ (1) зм³нна x çàì³íÿºòüñÿ íà

. (3)

Òîä³

. (4)

³ з врахуванням (2) можна записати, що:

. (5)

В формул³ (2) коеф³ц³ºнти A_i та абсциси ( вузли ) t_i вибираються в залежност³ в³д числа цих вузл³в). Значення n нев³домих t_i º коренями так званих пол³ном³в Лежандра. Вузли t_i розташован³ на ³нтервал³ (-1,1), завжди симетрично в³дносно нуля. Вс³ вагов³ коеф³ц³ºнти додатн³, а ¿х сума дор³внюº 2.

n	i	ti	Ai
1	1	0	2
2	1 ; 2	0,57735027	1
3	1 ; 3 2	0,77459667 0	5/9 8/9
4	1 ; 4 2 ; 3	0,86113631 0,33998104	0,34785484 0,65214516
5	1 ; 5 2 ; 4 3	0,906179846 0,538469310 0	0,236926885 0,478628670 0,568888889

Для достатньо гладко¿ п³д³нтегрально¿ функц³¿ формула Гауса (5) забезпечуº високу точн³сть вже при невеликому числ³ вузл³в n . Для оц³нки похибки обчислень за формулою Гауса з n вузлами користуються формулою:

, .

Наприклад, при

n=2 ;

n=3 .