Статистические модели в виде нелинейных полиномов

При составлении статистических моделей объектов химической техно­логии нередко возникает необходимость использовать нелинейную форму связи, чаще - параболу второй, третьей или более высоких степеней, ре­же - логарифмическую, гиперболическую, степенную иди показательную функциональные зависимости. В таких случаях применяют метод регресси­онного анализа, который с учетом особенностей конкретных объектов при­обретает ту или иную разновидность. Чаще всего использую так называе­мый метод классического регрессионного анализа для составления статис­тической модели в виде полинома второй (или более высокой) степени.

Определение коэффициентов в уравнении, например, для полинома второй степени при n переменных, производят приемами, аналогичными рассмотренным ранее. Однако в этом случае не требуется находить выбо­рочные коэффициенты корреляции, которые при нелинейной форме зависи­мости между исследуемыми переменными теряют смысл. Итак, если степень полинома выбрана заранее, то коэффициенты регрессии определяются по методы наименьших квадратов, а исследование уравнения проводится по статистическим критериям (в частности, адекватность модели устанавли­вается по критериям Фишера, как и в случае линейной регрессии).

Метод классического регрессионного анализа достаточно успешно применяется при составлении математических моделей химико-технологи­ческих, металлургических и других процессов.

В Excel линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных.

Расчет коэффициентов регрессионного уравнения b_J осуществляется методом наименьших квадратов, суть которого описана выше.

После вычисления коэффициентов регрессии переходят к статистическому анализу этого уравнения, который включает следующие этапы:

• оценивается адекватность модели (способность достоверно описывать функцию отклика);

• оценивается значимость факторов, входящих в уравнение регрессии.

Проверка адекватности регрессионного уравнения осуществляется с помощью критерия Фишера (F_P) по условию:

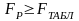(3.11)

где

(3.12)

где - дисперсия среднего;

(3.13)

- дисперсия адекватности.

(3.14)

где N – количество экспериментальных точек;

m – число коэффициентов регрессии в уравнении, включая свободный член

Таким образом, чем больше будет массив данных исходных данных, собранных в Табл.4.3 (величина N), и проще будет вид регрессионного уравнения (величина m), тем будет выше вероятность того, что получаемое уравнение регрессии будет адекватно. Следует отметить, что в соответствии с принципами статистики, недопустимы попытки получения сложного уравнения регрессии по небольшому количеству экспериментальных данных, например, расчет уравнения линии по одной точке или параболы – по двум, т.е. всегда должно соблюдаться условие: N>m.

Оценка значимости факторов, используемых при описании функции отклика осуществляется с помощью критерия Стьюдента (t_P) по условию:

(3.15)

где

(3.16)

где b_J – коэффициент регрессии при оцениваемом факторе;

– среднеквадратическое отклонение коэффициента регрессии.

Обычно величина критерия Стьюдента находится в пределах 2-4, поэтому, если среднеквадратическое отклонение коэффициента регрессии будет больше 25-50% величины самого коэффициента регрессии (по модулю), то данный коэффициент считается незначимым и может быть исключен из уравнения регрессии.

После исключения всех незначимых членов, уравнение регрессии приобретает новый вид. Следовательно, на следующем шаге необходимо будет снова оценить коэффициенты регрессии и снова проверить их значимость. Данный цикл операций производится до тех пор, пока не будет получено адекватное регрессионное уравнение, все факторы которого являются значимыми.

Следует отметить, что при моделировании ХТС допускается использовать только адекватные математические модели процессов во всем диапазоне изменения входных параметров вне зависимости от того, является модель физико-химической или статистической.

Пример 3.3. В результате анализа выборки (Табл.3.6)

Таблица 3.6

Исследуемая выборка

Время	Т окр.ср	Р1	V	C1	C2	C3	РН1	РН3	Р1
2	188	3,6	3,53	0,5	0,74	0,05	3	2	3,6
4	188	3,57	3,51	0,49	0,7	0,05	3	2	3,57
11	187	3,22	3,08	0,93	0,96	0,07	2	3	3,22
12	187	3,43	3,3	0,88	0,94	0,07	2	3	3,43
13	187	3,43	3,29	0,91	0,96	0,07	2	3	3,43
19	187	3,45	3,4	0,43	0,66	0,05	3	2	3,45
20	187	3,45	3,39	0,43	0,66	0,05	3	2	3,45

для управления процессом сделано предположение о наличии зависимости между факторами С1-РН1, РН3, V, Р1; С2-РН1, РН3, V, Р1; С3-РН1, РН3, V, Т, Р1 и взаимовлияние Т-Р1, V, РН1, РН3 и РН3-Р1, РН1. Определить количественные характеристики зависимости.