
Граф G задается множеством точек или вершин x1, х2 ,.., хn (которое обозначается через X) и множеством линий или ребер а1, а2,.., аm (которое обозначается символом А), соединяющих между собой все или часть этих точек. Таким образом, граф G
полностью задается (и обозначается) парой (X, А).
Если ребра из множества А ориентированы, что обычно показывается стрелкой, то они называются дугами, и граф с такими ребрами называется ориентированным графом (рис. 1.1). Если ребра не имеют ориентации, то граф называется неориентированным (рис. 1.2).
Другое, употребляемое чаще описание ориентированного графа G состоит в задании множества вершин X и соответствия Г, которое показывает, как между собой связаны вершины. Соответствие Г называется отображением множества X в X, а граф в этом случае обозначается парой G = (X, Г). Для графа на рис. 1.1 имеем Г (х1) = {х2, х5}, т. е. вершины х2 и х5 являются конечными вершинами дуг, у которых начальной вершиной является х1.
Г (х2) = {х1, х3},
Г (х3) = {х1},
Г (х4) = пустое множество,
Г (х5) = {х4}.
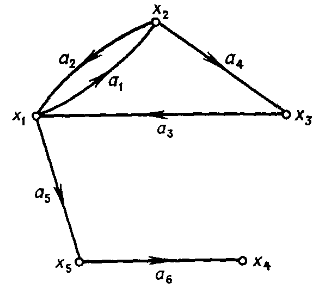
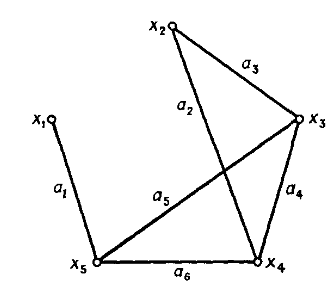
Рис. 1.1 Рис. 1.2
В случае неориентированного графа или графа, содержащего и дуги, и неориентированные ребра (см., например, графы, изображенные на рис. 1.1), предполагается, что соответствие Г задает такой эквивалентный ориентированный граф, который получается из исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Так, например, для графа, приведенного на рис. 1.2, имеем Г (х5) = {х1, х3, х4}, Г (x1)= {х5} и т. д.
Поскольку Г (хi) представляет собой множество таких вершин xj из X, для которых в графе G существует дуга (хi, xj), то через Г-1 (хi) естественно обозначить множество вершин xk, для которых в G существует дуга (xk, хi). Отношение Г-1 (хi) принято называть обратным соответствием. Для графа, изображенного на рис 1.1 , имеем
Г-1 (х1) ={x2, х3},
Г-1 (х2) ={х1}
и т. д.
Когда отображение Г действует не на одну вершину, а на множество вершин
Xq = {х1, х2, . . ., хq}, то под Г(Хq) понимают объединение
Г(х1) U Г(х2) U … U Г (хq),
т. е. Г(Хq) является множеством таких вершин xj из Х, что для каждой из них существует дуга (xi, хj) в G, где xi из Xq. Для графа, приведенного на рис. 1.1, Г ({х2, х5}) = {х1, х3, х4} и Г ({х1, х3}) = {х2, х5, х1}
Эйлеровы графы
Связный (Если каждую вершину графа можно соединить с любой другой его вершиной некоторой цепью, то граф называется связным.) граф G называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро; такая цепь называется эйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось только один раз. Если снять ограничение на замкнутость цепи, то граф называется полуэйлеровым; при этом каждый эйлеров граф будет полуэйлеровым.
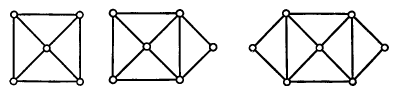
Рис 4.1 Рис. 4.2 Рис 4.3
при этом каждый эйлеров граф будет полуэйлеровым. На рис. 4.1, 4.2 и 4.3 изображены соответственно не эйлеров, полуэйлеров и эйлеров графы. Заметим, что предположение о связности графа G введено только ради удобства, так как оно позволяет не рассматривать тривиальный случай графа, содержащего несколько изолированных вершин.
Лемма. Если степень каждой вершины графа G не меньше двух, то G содержит цикл.
Доказательство. Если в графе G имеются петли или кратные ребра, то утверждение очевидно; поэтому предположим, что G является простым графом. Пусть v — произвольная вершина графа G; построим по индукции маршрут v → v1→ v2 ... , выбирая вершину v1 смежной вершине v, а для i ≥1 — выбирая vi+1 смежной vi и отличной от
vi-1 (существование такой вершины vi+1 гарантировано условием леммы). Так как G имеет конечное число вершин, то в конце концов мы придем к вершине, которая уже была выбрана раньше. Предположим, что vk — первая такая вершина; тогда часть маршрута, лежащая между двумя вхождениями vk, и является требуемым циклом.
Теорема. Связный граф G является эйлеровым тогда и только тогда, когда каждая вершина в G имеет четную степень.
Доказательство. => Предположим, что Р является эйлеровой цепью в графе G. Тогда при всяком прохождении цепи Р через любую из вершин графа степень этой вершины увеличивается на два. А так как каждое ребро встречается в Р ровно один раз, то каждая вершина должна иметь четную степень.
<= Проведем доказательство индукцией по числу ребер в G. В силу связности G, степень каждой вершины не меньше двух, а отсюда, по предыдущей лемме, заключаем, что граф G содержит цикл С. Если С проходит через каждое ребро графа G, то доказательство завершено; если нет, то, удаляя из G ребра, принадлежащие циклу С, получим новый (быть может, и несвязный) граф Н. Число ребер в Н меньше, чем в G, и любая вершина в Н по-прежнему имеет четную степень Согласно индуктивному предположению, в каждой компоненте графа Н существует эйлерова цепь. В силу связности графа G, каждая компонента в Н имеет по крайней мере одну общую вершину с циклом С, поэтому искомую эйлерову цепь графа G можно получить так: идем по ребрам цикла С до тех пор, пока не встретим неизолированную вершину графа Н, затем следуем по эйлеровой цепи той компоненты в Н, которая содержит указанную вершину; далее продолжаем путь по ребрам цикла С, пока не встретим вершину, принадлежащую другой компоненте графа Н, и т. д.; заканчивается процесс тогда, когда мы попадаем обратно в начальную вершину (см. рис. 4.4).
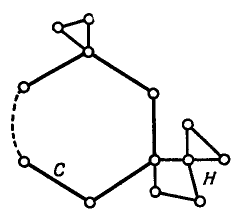
Рис. 4.4
Модифицируя данное доказательство, легко получить следующие два следствия:
Следствие 1. Связный граф является эйлеровым тогда и только тогда, когда семейство его ребер можно разбить на непересекающиеся циклы.
Следствие 2. Связный граф является полуэйлеровым тогда и только тогда, когда в нем не более двух вершин имеют нечетные степени.
Заметим, что если полуэйлеров граф содержит ровно две вершины с нечетными степенями, то в любой полуэйлеровой цепи (смысл этого понятия очевиден) одна из этих вершин обязательно будет начальной, а другая — конечной. По лемме о рукопожатиях граф не может иметь только одну вершину нечетной степени.
Теорема (алгоритма Флёри). Пусть G — эйлеров граф; тогда следующая процедура всегда возможна и приводит к эйлеровой цепи графа G. Выходя из произвольной вершины и, идем по ребрам графа произвольным образом, соблюдая лишь следующие правила:
стираем ребра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются;
на каждом этапе идем по мосту только тогда, когда нет других возможностей.
Доказательство. Покажем сначала, что указанная процедура может быть выполнена на каждом этапе. Предположим, что мы достигли некоторой вершины v; тогда если v ≠ u, то оставшийся подграф Н связен и содержит ровно две вершины нечетной степени, а именно u и v. Согласно следствию 2, граф Н содержит полуэйлерову цепь Р из v в u. Поскольку удаление первого ребра цепи Р не нарушает связности графа Н, отсюда следует, что описанное в теореме построение возможно на каждом этапе. Если же v = u, то доказательство остается тем же самым до тех пор, пока есть еще ребра, инцидентные вершине u.
Осталось только показать, что данная процедура всегда приводит к полной эйлеровой цепи. Но это очевидно, так как в G не может быть ребер, оставшихся непройденными после использования последнего ребра, инцидентного и (в противном случае удаление некоторого ребра, смежного одному из оставшихся, привело бы к несвязному графу, что противоречит (2)).
