61

4.2. Примеры решения типовых задач

Часть I

Пример 1. Найдите область определения функции .

Решение.

Ответ: .

Пример 2. Построить графики зависимости спроса Q_D(P) и предложения Q_S(P) от цены на товар Р , и найти при какой цене спрос равен предложению, если Q_D(P)= ; Q_S(P)= .

Р ешение.

Построим в плоскости РОQ графики функций спроса и предложения (см. рисунок). В точке равновесия А (точке пересечения графиков) спрос равен предложению. Для нахождения координат этой точки решим систему:

Из этой системы получаем: 

Ответ: P=2; Q=1.

Пример 3. Вычислить предел .

Решение.

= = .

Ответ: .

Пример 4. Вычислить предел .

Решение.

= =

Ответ: .

Пример 5. Найти и построить асимптоты графика функции .

Решение. Так как точка разрыва , а ; ,

то - вертикальная асимптота.

Наклонные асимптоты можно задать уравнением , где , .

Если оба предела существуют, то наклонная асимптота (при этом, если - имеем горизонтальную асимптоту).

;

.

Следовательно, - наклонная асимптота.

Ответ: ,

Пример 6. Используя правила вычисления производной и таблицу, найдите производные следующих функций:

а) ; б) ; в)

Решение.

а) ;

б) ; в) .

Ответ:

а) ; б) ; в) .

Пример 7. Используя правило Лопиталя, найдите предел

Решение. .

Ответ: .

Пример 8. Составьте уравнение касательной к графику функции в точке ,

постройте графики кривой и касательной к ней:

Решение. Уравнение касательной в точке имеет вид .

; ; . Подставляя полученные данные в уравнение касательной, получим: .

Ответ:

Пример 9. Используя дифференциал функции, найдите приближенное значение величины .

Решение. Приближенное значение искомой величины ищем по формуле линеаризации .

Будем рассматривать как значение величины функции , при . Полагаем , представим как , где . Тогда , , , Подставляя полученные данные в формулу линеаризации, получаем .

Ответ:

Пример10.1 Найдите экстремум функции .

Решение. Найдем стационарные (критические) точки функции: ; ; , .

Найдем значение второй производной в критических точках: , , т.к. , то - будет точкой минимума; т.к. , то - будет точкой максимума.

Функция имеет максимум в точке , равный 2, и минимум в точке , равный 2.

Ответ: , .

Пример10.2. Найдите наибольшее и наименьшее значение функции на отрезке .

Решение. Найдем критические точки функции на данном отрезке и вычислим значения функции в этих точках и в граничных точках отрезка:

; , ,

, , .

Выберем из найденных значений наибольшее и наименьшее.

Ответ: , .

Пример11.

Провести полное исследование и построить график функции

Решение.

1. Функция определена и непрерывна для всех действительных значений х, кроме х=6.

2. График функции несимметричен, так как функция не является ни четной, ни нечетной. Функция также не является периодической.

3. График функции пересекает ось Ох в точках (5; 0); (7; 0).Чтобы найти эти точки, нужно решить уравнение .

График функции пересекает ось Оу в точке . Чтобы найти эту точку, нужно подставить в уравнение заданной функции значение .

4. Найдем интервалы знакопостоянства функции, решив неравенства

а) ; б) .

Итак, если ; , если ;

5. Рассмотрим поведение функции на границах области определения.

Как ведет себя функция вблизи точки разрыва х = 6 ?

Чтобы ответить на этот вопрос, найдем и . Следовательно, прямая является вертикальной асимптотой графика функции.

Как ведет себя функция при и при ?

Если рациональная функция представима в виде , где - бесконечно малая функция при (то есть ), то функция является наклонной асимптотой для графика функции . Функция представлена в виде суммы линейной и бесконечно малой функций , следовательно, прямая является для графика заданной функции наклонной асимптотой.

График функции приближается к прямой .

6. Интервалы монотонности и экстремумы найдем, используя теорию первой производной:

для любых значений аргумента из области определения. Вывод: функция монотонно убывает на всей области определения, экстремумов не имеет.

7. Исследование функции на выпуклость и точки перегиба проведем с помощью второй производной ;

Определим знак второй производной.

если , то на интервале график функции направлен выпуклостью вверх;

е сли , то на интервале график функции направлен выпуклостью вниз. Точек перегиба кривая не имеет. Используя проведенное исследование, строим график функции .

Приведем еще один пример исследования функции и построения графика.

Провести полное исследование и построить график функции .

Решение

1. Функция определена и непрерывна для всех действительных значений х, кроме х=6.

2. График функции несимметричен, так как функция не является ни четной, ни нечетной. Функция также не является периодической.

3. График функции не пересекает ось Ох, так как уравнение действительных корней не имеет. График функции пересекает ось Оу в точке .

4. Найдем интервалы знакопостоянства функции, решив неравенства

а) ;

б) .

Итак, ; .

5. Рассмотрим поведение функции на границах области определения.

Как ведет себя функция вблизи точки разрыва ?

Чтобы ответить на этот вопрос, найдем и . Следовательно, прямая является вертикальной асимптотой графика функции.

Как ведет себя функция при ?

График функции приближается к прямой , которая является для графика наклонной асимптотой. (Если рациональная функция представима в виде , где - бесконечно малая функция при , то функция является наклонной асимптотой для графика функции . Функция представлена в виде суммы линейной и бесконечно

малой функций, следовательно, прямая является для графика заданной функции наклонной асимптотой).

6. Интервалы монотонности и экстремумы данной функции найдем, используя теорию первой производной. Производная первого порядка имеет вид: .

, следовательно, на этих интервалах функция монотонно убывает;

, следовательно, на этих интервалах функция монотонно возрастает.

На интервале производная ;

на интервале производная ;

причем , следовательно, точка является точкой локального минимума исследуемой функции.

На интервале производная ;

на интервале производная ;

причем , следовательно, точка является точкой локального максимума исследуемой функции.

7. Исследование функции на выпуклость и точки перегиба проведем с помощью

второй производной ;

если , следовательно, на интервале график функции направлен выпуклостью вверх;

если , следовательно, на интервале график функции направлен выпуклостью вниз. Точек перегиба кривая не имеет. Используя проведенное исследование, строим график заданной функции.

Пример 12. Решить методом Гаусса систему уравнений:

Решение. Для того, чтобы решить систему линейных алгебраических уравнений, применим метод Гаусса, состоящий в последовательном исключении неизвестных с помощью элементарных преобразований.

1) Переставим второе уравнение с первым, чтобы коэффициент перед переменной х в первом уравнении системы был равен 1, получим:

2) Исключим переменную x из второго и третьего уравнений системы. Для этого умножим первое уравнение системы на (–2) и сложим со вторым уравнением; умножим первое уравнение на (–3) и сложим с третьим уравнением, получим систему в следующем виде:

3) Разделим второе уравнение на (–7), чтобы коэффициент перед переменной y во втором уравнении был равен 1:

4) Исключим переменную y из третьего уравнения системы. Для этого умножим второе уравнение на 5 и сложим с третьим уравнением:

5) Разделим третье уравнение на ( ) и получим значение переменной z:

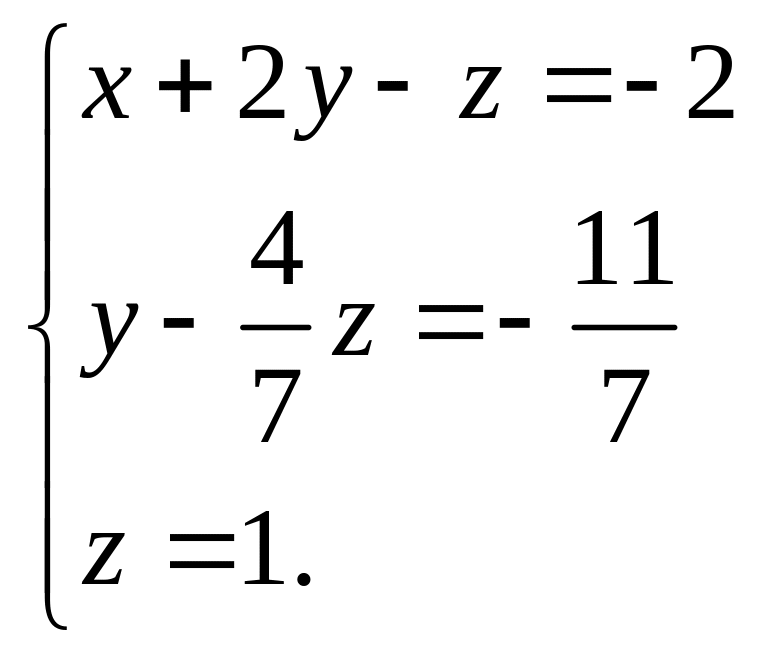
6) Подставим значение z=1 во второе уравнение системы и найдём значение переменной y:

7) Подставим значения z=1 и y=-1 в первое уравнение системы и получим:

Ответ: .

Пример 13. Даны векторы и . Определить, при каких и векторы и коллинеарны.

Решение. Векторы, заданные координатами, коллинеарны, если их координаты пропорциональны, т.е. .

Отсюда  = 4;  = 1. Ответ: =4; = 1.

Пример 14. Разложите вектор по векторам

Решение. Разложить вектор по векторам , - значит представить его в виде , где ; ; , , . Решив систему двух уравнений с двумя неизвестными, получим

Следовательно, . Ответ:

Пример 15. Даны векторы ={1; -2; 1} и ={-1; 1; -2}. Найдите косинус угла между векторами и .

Решение. Применяя линейные операции, найдём векторы и :

={ }={5; -8; 7},

={ }={-1; -1; -4}.

По формуле косинуса угла между векторами получаем:

Ответ: = .

Пример 16. Заданы координаты вершин треугольника АВС:

А(-1;2); В(-3;5); С(-7;0).Составить уравнение медианы и высоты треугольника, проведенных через вершину В.

Решение.

1. Медианой ВМ треугольника АВС является отрезок, соединяющий вершину В треугольника с серединой противоположной стороны М. Найдем координаты точки М как середины стороны АС: .

Составим уравнение медианы ВМ треугольника АВС как уравнение прямой, проходящей через две заданные точки: В(-3;5) и М(–4;1).

Уравнение прямой ВМ: .

2. Высотой ВК треугольника АВС является отрезок перпендикуляра, опущенного из вершины В треугольника на противоположную сторону АС треугольника (или ее продолжение). При решении задачи используем тот факт, что вектор нормали прямой АС, является направляющим вектором искомой прямой. Найдем вектор нормали прямой АС.Составим уравнение прямой АС как уравнение прямой, походящей через две заданные точки А ( -1; 2) и С(-7; 0): . Вектором нормали к этой прямой АС является вектор . Далее составим уравнение прямой, проходящей чрез точку В(-3; 5) параллельно найденному вектору , используя условие коллинеарности векторов и : .

Ответ: 1.уравнение медианы треугольника ;

2: уравнение высоты треугольника .

Пример 17. Заданные уравнения 1) ;

2) ; 3)

привести к каноническому виду и построить кривые, координаты точек которых удовлетворяют этим уравнениям:

Решение

1). Для того чтобы уравнение привести к каноническому виду, сгруппируем переменные х и у и выделим полный квадрат в выражениях: и .

; ;

. Получили приведенное к каноническому виду уравнение окружности с центром в точке (-3; 2) и радиусом R = 3. (рис 1.)

Решение

2). Для того чтобы уравнение привести к каноническому виду, сгруппируем переменные х и у и выделим полный квадрат в выражении: .

Получили приведенное к каноническому виду уравнение эллипса

с центром в точке (-1;0) и полуосями а = 3; в = 1. (рис 2.)

Решение

3). Для того чтобы уравнение привести к каноническому виду, сгруппируем переменные х и у и выделим полный квадрат в выражениях: и .

Получили приведенное к каноническому виду уравнение гиперболы

с центром (-2;1) и полуосями а = 4; в = 3. (рис 3)

Рис.1

Рис.2

Рис.3

Пример 18.

Составить уравнение плоскости, проходящей через точку М(-3; 1; 2) перпендикулярно вектору , если Р(1; -3; -1).

Решение. Уравнение плоскости, п оходящей через точку перпендикулярно вектору имеет вид: п.

Найдем вектор .

Составим уравнение плоскости, проходящей через точку перпендикулярно вектору .

. Раскроем скобки, приведем подобные члены и получим уравнение искомой плоскости .

Ответ: .

Пример 19.Составить канонические уравнения прямой, проходящей через точку М(2; -1; 3) параллельно вектору .

Решение.

Канонические уравнения прямой, проходящей через точку параллельно вектору , имеет вид: .

Составим канонические уравнения прямой, проходящей через точку параллельно вектору .

Ответ: .

Пример 20.

Найти координаты точки пересечения прямой, заданной параметрически

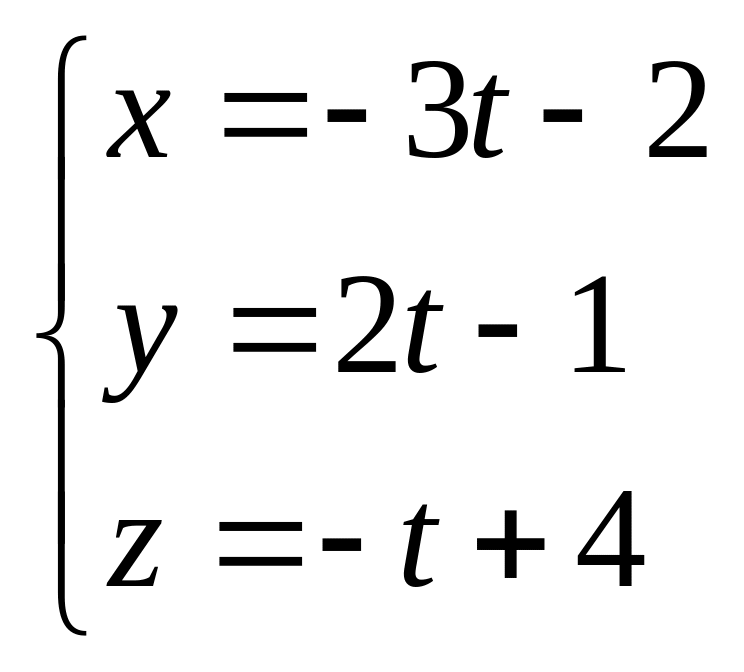с плоскостью .

Решение.

Координаты искомой точки удовлетворяют и уравнению прямой, и уравнению плоскости. Поэтому являются решением системы:

Решим эту систему относительно неизвестной .

Подставим из первых уравнений в последнее, получим:

. Решая это уравнение, найдем =1.

Затем найдем искомые координаты .

Ответ: .