30

1. Введение.

Буквально во всех сферах своей деятельности человек ставит определенные цели и пытается достичь их наилучшим (оптимальным) образом. Область математики, называемая тождественными терминами «Исследование операций», «Математическое программирование» и «Методы оптимизации», разрабатывает методы принятия наилучших решений, называемые методами оптимизации. Методы оптимизации применимы в любой области человеческой деятельности при условии, что реальная проблема математически формализована. Последнее означает, что существует достаточно адекватная математическая модель поставленной задачи, включающая:

1. цель, которая должна быть достигнута;

2. параметры оптимизации, управляя которыми можно достичь цель;

3. ограничения на параметры оптимизации (если есть), которые должны быть удовлетворены .

Количественной мерой достижения поставленной цели является целевая функция, аргументами которой являются параметры оптимизации. Ограничения могут быть связаны с ограниченностью каких-то ресурсов, быть следствием физических законов или требований к оптимизируемому

объекту.

2. Основные понятия.

2.1. Постановка задачи оптимизации.

Найти ( 2.1.0 )

при ограничениях

Где

x - вектор параметров минимизации x(x₁, x₂, … ,x_n) такой, что является допустимым решением (допустимой точкой) задачи (2.1.1).

- целевая функция, определенная на ; целевая функция является скалярной функцией n вещественных переменных.

- множество допустимых решений (допустимое множество), определяемое наличием ограничений. Для конечномерных задач, которые будут рассматриваться, лежит в евклидовом пространстве ( ).

При отсутствии ограничений на изменение оптимизируемых параметров допустимое множество совпадает с . В этом случае задачу минимизации называют задачей безусловной минимизации (безусловной экстремальной задачей). В противном случае, когда , имеем задачу условной минимизации (условную экстремальную задачу). Допустимое множество может быть задано различными способами. В наиболее общем случае допустимое множество описывается системой уравнений и неравенств, связывающих значения параметров оптимизации x. Ограничения в виде уравнений называют ограничениями типа равенств, а неравенства - ограничениями типа неравенств.

В соответствии с теоремой Вейерштрасса решение задачи (2.1.1) существует.

Теорема Вейерштрасса.

Пусть - замкнутое ограниченное множество в , 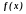- непрерывная функция, определенная на множестве . Тогда точка глобального минимума функции на существует.

Обозначим решение задачи минимизации. Если не унимодальна на (т.е. имеет более одного минимума), то точка может быть точкой глобального или локального минимума.

Точка называется

1) точкой глобального минимума функции на множестве или глобальным решением задачи ( 2.1 .0 ), если

( 2.1.0 )

2) точкой локального минимума функции на множестве или локальным решением задачи ( 2.1 .0 ), если

,такое что для ( 2.1.0 )

где

Если неравенство в ( 2.1 .0 ) или в ( 2.1 .0 ) выполняется как строгое при то - точка строгого минимума (строгое решение) в глобальном или локальном смысле. При равенстве в ( 2.1 .0 ) или в ( 2.1 .0 ) существует некоторая окрестность точки , в которой

Для отражения того факта, что точка является точкой глобального минимума функции на множестве , обычно используется запись

или эквивалентная ей запись

Множество всех точек глобального минимума на , обозначают через

где - минимальное значение функции на множестве .

Если по смыслу задачи оптимизации требуется найти максимум целевой функции, задачу максимизации сводят к задаче минимизации, изменив знак целевой функции. Таким образом, задача максимизации

, ( 2.1.0 )

решается в виде эквивалентной ей задачи минимизации

_.

Универсального метода решения поставленной задачи не существует. Выбор методов решения определяется особенностями целевой функции и ограничений. Если целевая функция и ограничения линейны, имеет место задача линейного программирования. Если или целевая функция или ограничения или и то и другое нелинейны, имеем задачу нелинейного программирования. Линейное и нелинейное программирование, являясь достаточно самостоятельными разделами математического программирования, существенно отличаются методами решения задачи оптимизации.