
- •Глава 1. Линейная и векторная алгебра
- •Глава 2. Системы координат
- •Глава 3. Прямая на плоскости
- •Глава 4. Плоскость в пространстве
- •Глава 5. Прямая в пространстве
- •Глава 6. Кривые второго порядка
- •Глава 7. Поверхности второго порядка
- •Глава 8. Дифференциальная геометрия
- •Глава 9. Предел функции в точке
- •Глава 10. Дифференциальное исчисление функции одной переменной
- •Глава 11. Функции нескольких переменных
- •Глава 12. Неопределенный интеграл
- •§1 Основные методы интегрирования
- •Глава 13. Определенный интеграл
Глава 10. Дифференциальное исчисление функции одной переменной
|
|||||||
1.
2.
3.
4.
5.
6.
|
7.
8.
9.
10.
11.
12.
|
13.
14.
15.
16.
17.
18.
|
|||||
|
|||||||
Пусть
функции
1. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций:
2. Производная произведения двух функций равна:
3. Производная частного двух функций равна:
|
Задача. Найти
производные функций
Решение. Воспользуемся формулой производной частного:
Аналогичным образом получим формулу
|
||||||
|
|||||||
Пусть
Теорема.
Если
функция
имеет в некоторой точке
производную
|
Задача. Найти
производную функции
Решение. Представим
функцию как сложную, введя промежуточный
аргумент
:
|
||||||
|
|||||||
Теорема.
Если функция
производную
|
Задача. Найти
производную обратных тригонометрических
функций
Решение. Пусть
где
перед корнем взят знак +, так как
Итак,
|
||||||
|
|||||||
Если
функция задана неявным уравнением
|
Задача. Найти
производную функции
,
заданную уравнением
Решение. Функция задана неявно. Дифференцируя обе части этого тождества по , считая, что есть функция от и, пользуясь правилом дифференцирования сложной функции, получим
|
||||||
|
|||||||
На
практике встречаются функции,
производные которых находят
логарифмическим дифференцированием.
К их числу относится так называемая
степенно-показательная
функция
Найдем производную, предварительно логарифмируя:
|
Задача.
Решение. Найдем
логарифм данной функции
Отсюда
Задача.
Решение. Прологарифмируем данное равенство
Дифференцируя обе части последнего равенства, получим
|
||||||
|
|||||||
Если функция аргумента задана параметрическими уравнениями
то производная функции по переменной , т.е. вычисляется по формуле:
|
Задача.
Решение. Найдем
|
||||||
|
|||||||
Уравнение
прямой, касательной к графику
Уравнение
нормали, т.е. прямой, проходящей через
точку
|
Задача. Составить
уравнение касательной и нормали к
параболе
Решение. Найдем
производную функции
при
В
результате получим искомые уравнения
касательной
|
||||||
|
|||||||
Дифференциал любой дифференцируемой функции равен произведению ее производной на дифференциал независимой переменной.
|
Задача. Найти
дифференциал функции
Решение.
|
||||||
10 Приближенное вычисление с помощью дифференциала |
|||||||
Если
|
Задача. Вычислить
приближенное значение
Решение. Рассмотрим
функцию
,
полагая
получим
Ответ. 0,513. |
||||||
11 Производные высших порядков |
|||||||
Производной
го
порядка называют производную от
производной
|
Задача. Найти
Решение.
Ответ. 60. |
||||||
12 Производные высших порядков, заданных параметрически |
|||||||
Если
функция задана параметрически, то
производные
|
Задача. Найти
Решение.
|
||||||
13 Дифференциалы высших порядков |
|||||||
Дифференциалом го порядка называется дифференциал от дифференциала го порядка:
или
|
Задача. Найти
дифференциалы второго и третьего
порядков функции
Решение.
|
||||||
|
|||||||
Пусть
функции
или
т.е.
частное
при условии, что существует предел отношения производных.
Правило
Лопиталя применяется для раскрытия
неопределенностей вида
и
.
Но на практике встречаются неопределенности
вида
|
Задача. Найти
Решение. Здесь имеет место неопределенность . Применим правило Лопиталя, т.е. рассмотрим предел отношения производных заданных функций
Последний
предел дает неопределенность
Задача.
Найти
Решение.
Задача. Найти
Решение.
|
||||||
15 Теорема Ролля |
||||||||||||||||||||||
Теорема (Ролля). Пусть функция удовлетворяет следующим условиям:
1.
непрерывна на отрезке
2.
дифференцируема в интервале
3.
на концах отрезка принимает одинаковые
значения:
Тогда
внутри отрезка
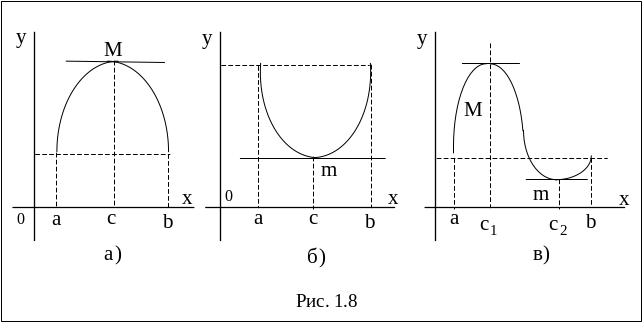
Геометрически
теорема Ролля означает, что на графике
функции
найдется хотя бы одна точка, в которой
касательная к графику параллельна
оси
|
Задача.
Выполняется
ли теорема Ролля для функции
Решение. Так
как функция
непрерывна и дифференцируема при всех
значениях
и ее значения на концах отрезка
Следовательно,
Ответ. выполняется, . |
|||||||||||||||||||||
16 Теорема Лагранжа |
||||||||||||||||||||||
Теорема (Лагранжа). Если функция 1. непрерывна на отрезке ,
2.
дифференцируема в интервале
Теорема
Лагранжа имеет простой геометрический
смысл. Отношение
|
Задача.
Проверить справедливость теоремы
Лагранжа для функции
Решение. Функция
определена при всех значениях
Найдем
точку с, для которой выполняется
равенство
|
|||||||||||||||||||||
17 Теорема Коши |
||||||||||||||||||||||
Теорема
(Коши).
Если функции
и
1. непрерывны на отрезке ,
2.
дифференцируемы в интервале
,
причем
|
||||||||||||||||||||||
18 Теорема Ферма |
||||||||||||||||||||||
Теорема
(Ферма).
Пусть функция
определена на интервале
|
||||||||||||||||||||||
19 Интервалы монотонности |
||||||||||||||||||||||
Теорема
(достаточные условия).
Если функция
дифференцируема в интервале
и
|
Задача. Определить
интервалы монотонности функции
Решение.
Найдем
Аналогично,
решая неравенство
Следовательно,
функция возрастает в промежутках
|
|||||||||||||||||||||
20 Экстремум функции |
||||||||||||||||||||||
Точки,
в которых производная
равна нулю или не существует, называются
критическими
точками
функции. Если дифференцируемая функция
y=f(x)
в точке
Т
|
Задача. Найти
экстремумы функции
Решение. Очевидно,
что
Из
таблицы видно, что в точке
|
|||||||||||||||||||||
21 Нахождение наибольшего и наименьшего значения функции |
||||
Для нахождения наибольшего и наименьшего значений функции на отрезке необходимо:
|
Задача. Найти
наибольшее и наименьшее значения
функции
Решение. Находим критические точки:
Наибольшее
значение функции при
Наименьшее значение функции при равно -8. |
|||
22 Вертикальная асимптота |
||||
Прямая
|
Задача. К |
|||
23 Горизонтальная асимптота |
||||
Прямая
|
Задача. Прямая
|
|||
24 Наклонная асимптота |
||||
Прямая y = kx + b – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.
|
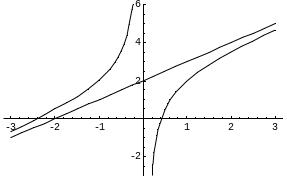
Задача. Найти
асимптоты и построить график функции
1) Вертикальные асимптоты: y+ x0-0: y- x0+0, следовательно, х = 0- вертикальная асимптота. 2) Наклонные асимптоты:
Таким образом, прямая у = х + 2 является наклонной асимптотой. Построим график функции:
|
|||
25 Мера плоского множества |
||||
Мера множества, математическое понятие, обобщающее понятия длины отрезка, площади плоской фигуры и объёма тела на множества более общей природы. В качестве примера можно привести определение меры Лебега (введённой А. Лебегом в 1902) для ограниченных множеств, лежащих на плоскости. При определении меры Лебега, так же как и при определении площади плоских фигур в геометрии, исходят из сравнения части плоскости, занимаемой множеством, с выбранной единицей измерения. |
||||
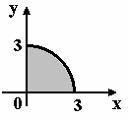
Задача. Мера
множества, изображенного на
рисунке,
Решение. Мерой
данного множества будет площадь
четверти круга, следовательно, если
площадь круга
Ответ. .
Задача. Мера плоского множества, изображенного на рисунке,
равна… Решение. Площадь
заштрихованного треугольника и будет
мера данного множества, следовательно,
используя геометрический смысл
определенного интеграла для нахождения
площади, получим:
Ответ. 1 |
||||

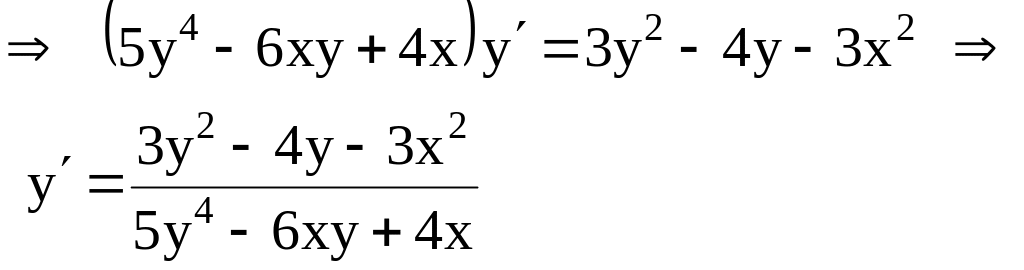
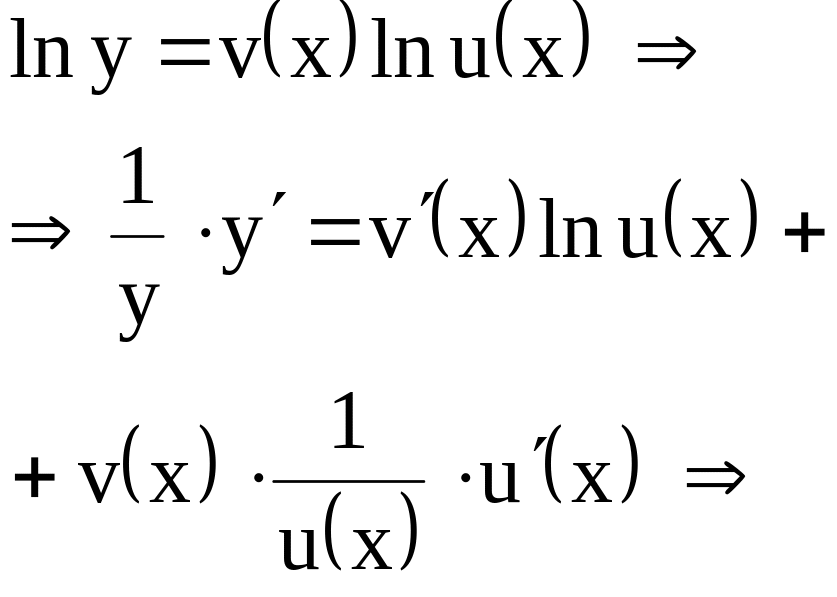
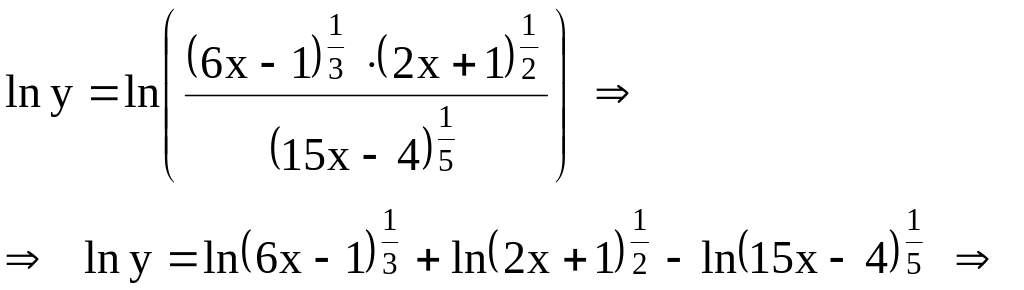
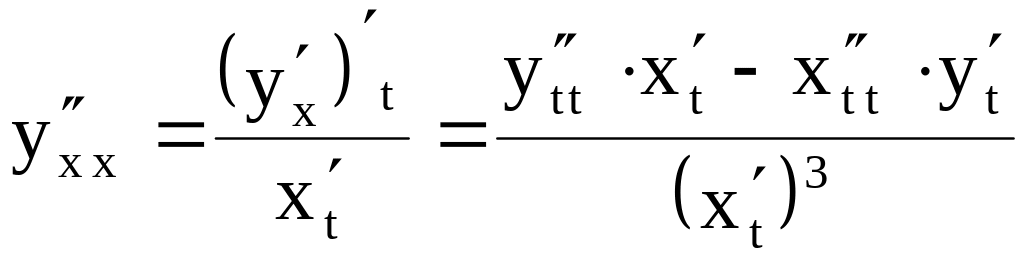
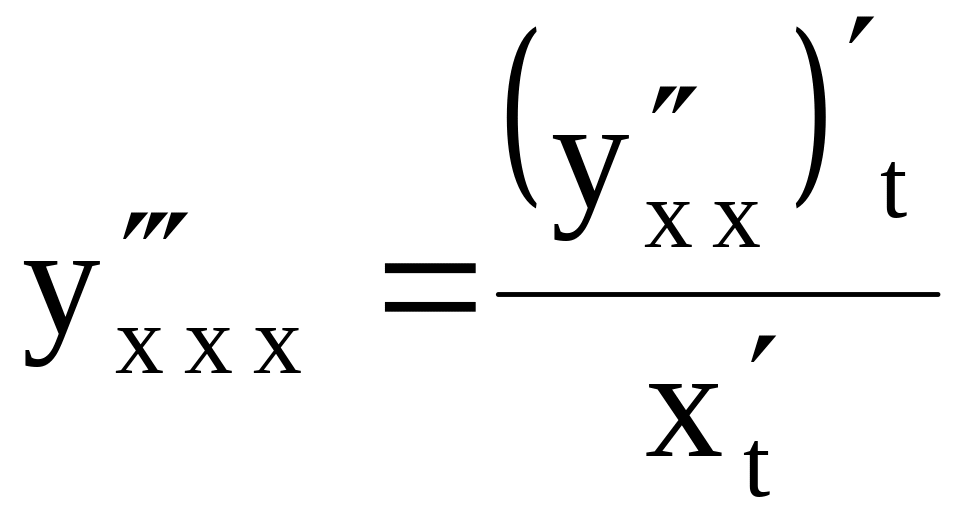
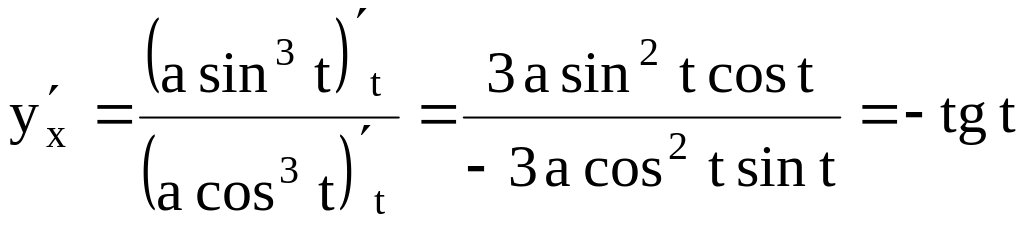
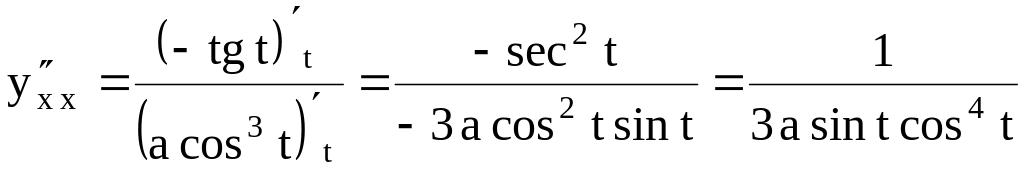 .
.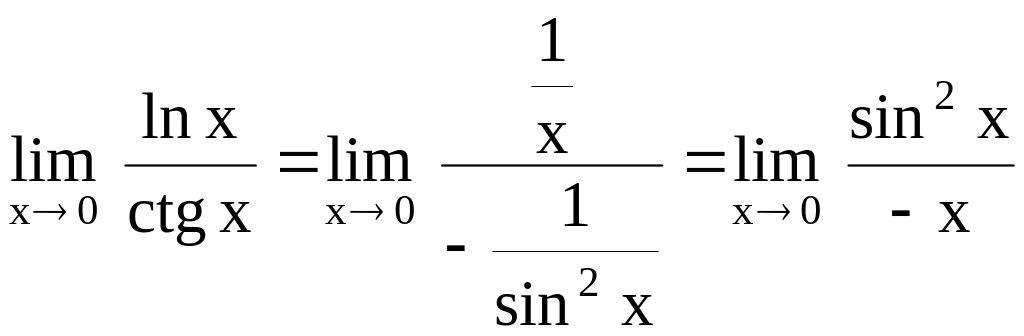 .
.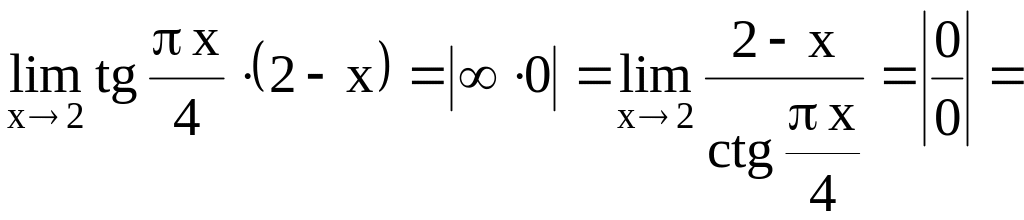
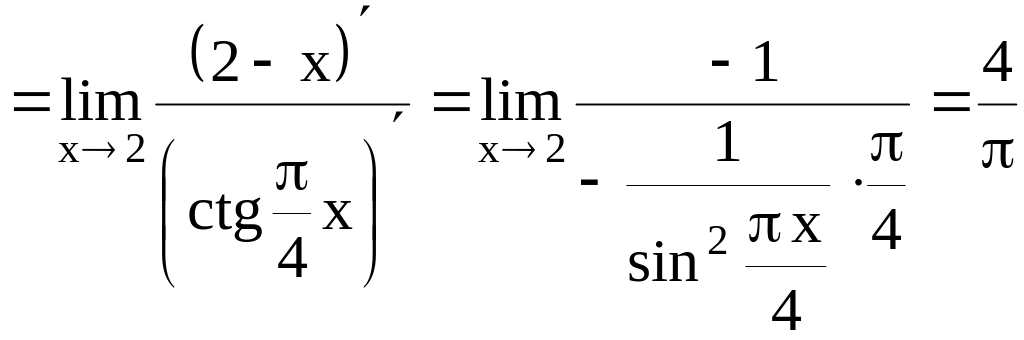 .
.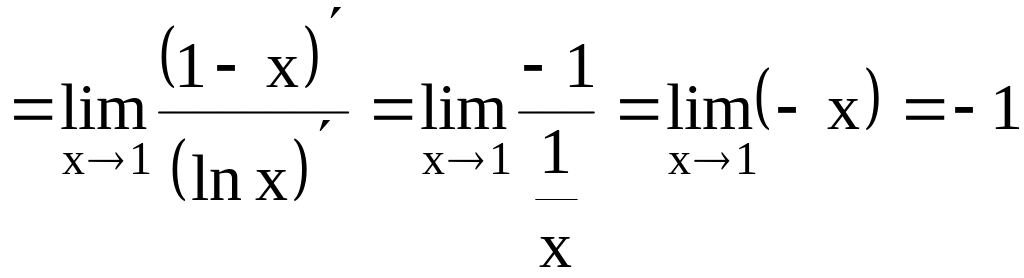 .
.

 еорема
(достаточное условие экстремума).
еорема
(достаточное условие экстремума).
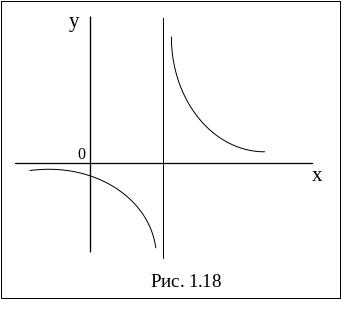 ривая
ривая
 равна…
равна…