2.2 Задание 2
Описание задачи
Две бригады готовят 10 самолетов к полету. Первая бригада – бригада механиков проверяет механическую часть самолета, а вторая бригада – бригада электронщиков проверяет электронное оборудование самолета. Для подготовки самолета к полету необходимо чтобы сначала первая бригада проверила механику, а затем вторая – электронное оборудование. Время (длительность) обслуживания каждого самолета бригадой механиков задается значениями вектора , а бригадой электронщиков вектора .
Найти такую последовательность проверки самолетов, чтобы время, затраченное на подготовку всех самолетов к полету, было бы минимальным.
Типовой пример выполнения задания 2
Дано: 10 самолетов, т. е. n = 10;
две бригады, т. е. m = 2;
значения длительностей осмотра каждого самолета каждой бригадой заданы следующей таблицей:
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
а ={ } |
9 |
4 |
16 |
12 |
13 |
5 |
2 |
2 |
14 |
15 |
b ={ } |
11 |
8 |
4 |
12 |
10 |
5 |
15 |
9 |
3 |
6 |
Решение
Если самолеты рассматривать как требования, бригаду механиков как прибор А, а бригаду электронщиков как прибор В, то решение задачи в рамках теории расписаний (ТР) сводится к решению задачи упорядочения 10 требований (n = 10) для двух приборов (m = 2). Поскольку каждый самолет обслуживается сначала 1-й, а затем 2-й бригадой (т. е. по такой очереди), это означает, что для обслуживания каждого самолета маршруты фиксированы и равны: (A, B). Это, в свою очередь, означает, что решается задача для системы обслуживания с одинаковыми маршрутами поточного типа (Flow Shop), обозначаемой в ТР как “F”. Так как в данной системе имеется два прибора А и В и критерий состоит в минимизации общего времени обслуживания Cmax, то рассматриваемая задача в рамках ТР сводится к задаче F2 || Cmax.
Эта задача решается с помощью одного из трех следующих алгоритмов.
Алгоритм 1
Шаг 1. Построим множество Na = {i N } и множество = {i N }.
Для нашего примера Na = {1, 2, 7, 8} и = {3, 4, 5, 6, 9, 10}.
Шаг 2. Сформируем перестановку * требований множества N, упорядочив сначала требования множества Na по неубыванию значений и вслед за ними упорядочив требования множества по невозрастанию значений :
Na |
|
||||||||
1 |
2 |
7 |
8 |
3 |
4 |
5 |
6 |
9 |
10 |
|
|
||||||||
9 |
4 |
2 |
2 |
4 |
12 |
10 |
5 |
3 |
6 |
Упорядочим требования множества Na по неубыванию значений , затем требования множества по невозрастанию значений :
ti |
2 |
2 |
4 |
9 |
12 |
10 |
6 |
5 |
4 |
3 |
i |
7 |
8 |
2 |
1 |
4 |
5 |
10 |
6 |
3 |
9 |
Конец алгоритма.
Итак, искомая
оптимальная перестановка, найденная
по алгоритму 1, будет
=
(7,
8, 2, 1, 4, 5, 10, 6, 3, 9).
Алгоритм 2
Шаг 1. Каждому требованию i N приписать вес
:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
а ={ } |
9 |
4 |
16 |
12 |
13 |
5 |
2 |
2 |
14 |
15 |
b ={ } |
11 |
8 |
4 |
12 |
10 |
5 |
15 |
9 |
3 |
6 |
– |
-2 |
-4 |
+12 |
0 |
+3 |
0 |
-13 |
-7 |
+11 |
+9 |
|
9 |
4 |
4 |
12 |
10 |
5 |
2 |
2 |
3 |
6 |
max {min{ } i N} = max{9, 4, 4,12, 10, 5, 2, 2, 3, 6}= 12.
Предположим. что w = 20 > 12. Вычислим веса:
w (1) = sgn(–2) · (20 – min{a1, b1}) = – (20 – 9) = –11;
w (2) = sgn(–4) · (20 – 4) = – (20 – 4) = –16;
w (3) = sgn(12) · (20 – 4) = (20 – 4) = 16;
w (4) = sgn(0) · (20 – 12) = (20 – 12) = 8;
w (5) = sgn(3) · (20 – 10) = (20 – 10) = 10;
w (6) = sgn(0) · (20 – 5) = (20 – 5) = 15;
w (7) = sgn(–13) · (20 – 2) = – (20 – 2) = – 18;
w (8) = sgn(–7) · (20 – 2) = – (20 – 2) = – 18;
w (9) = sgn(11) · (20 –3) = (20 – 3) = 17;
w (10) = sgn(9) · (20 –6) = (20 – 6) = 14.
Шаг 2. Построить перестановку *, упорядочив требования по неубыванию весов:
|
-18 |
-18 |
-16 |
-11 |
+8 |
+10 |
+14 |
+15 |
+16 |
+17 |
|
7 |
8 |
2 |
1 |
4 |
5 |
10 |
6 |
3 |
9 |
Конец алгоритма.
Итак, искомая
оптимальная перестановка, найденная
по алгоритму 2, тоже будет
=
=
(7,
8, 2, 1, 4, 5, 10, 6, 3, 9).
Алгоритм Джонсона
Шаг 1 (пункт 1). Выберем среди невычеркнутых элементов векторов a = (a1, a2…an) и b = (b1, b2…bn) минимальное число. Это a7 = 2.
Шаг 2 (пункт 2). Так как это минимальное число является элементом вектора a, то обслуживание 7-го требования назначаем первым по очереди и 7-й элемент вычеркиваем из векторов a и b.
Шаг 3. Не все и вычеркнуты, поэтому вернемся к пункту 1.
Шаги
4-6.
Выберем
среди невычеркнутых элементов векторов
и
минимальное число.
Это
=
2. Значит, обслуживание 8-го требования
назначаем первым среди невычеркнутых
(т. е. вторым по очереди) и 8-й элемент
вычеркиваем из векторов
и
.
Шаги
7-9.
Минимальное число
=
3, значит,
обслуживание 9-го требования назначаем
последним среди невычеркнутых (т. е.
десятым по очереди) и 9-й элемент
вычеркиваем из векторов
и
.
Шаги
10-12.
Минимальное число
=
4,
значит, обслуживание 2-го требования
назначаем первым среди
невычеркнутых (т. е. третьим по очереди)
и 2-й элемент вычеркиваем из векторов
и
.
Шаги
13-15.
Минимальное число
=
4, значит,
обслуживание
3-го требования назначаем последним среди невычеркнутых
(т. е. девятым по очереди) и 3-й элемент вычеркиваем из
векторов и .
Шаги
16-18.
Минимальное число
=
5, значит,
обслуживание
6-го требования назначаем первым среди невычеркнутых
(т. е. четвертым по очереди) и 6-й элемент вычеркиваем из
векторов и .
Шаги
19-21.
Минимальное число
=
6, значит,
обслуживание 10-го требования назначаем
последним среди невычеркнутых
(т. е. восьмым по очереди) и 10-й элемент вычеркиваем из
векторов и .
Шаги
22-24.
Минимальное число
=
9, значит,
обслуживание
1-го требования назначаем первым среди невычеркнутых (т. е. пятым по очереди) и 1-й элемент вычеркиваем из векторов и .
Шаги
25-27.
Минимальное число
=
10, значит,
обслуживание 5-го требования назначаем
последним среди невычеркнутых
(т. е. седьмым по очереди) и 5-й элемент вычеркиваем из
векторов и .
Шаги
28-30.
Минимальное число
=
12, значит,
обслуживание 4-го требования
назначаем первым среди
невычеркнутых
(т. е. шестым по очереди) и 4-й элемент вычеркиваем из
векторов и .
Шаг
31. Так
как все
и
вычеркнуты, то конец
алгоритма.
Итак, искомая оптимальная перестановка, найденная по алгоритму 3 – алгоритму Джонсона, будет
=
(7,
8, 2, 6, 1, 4, 5, 10, 3, 9).
Примечание – Решая данную задачу по трем алгоритмам, замечаем, что две оптимальные перестановки, полученные по двум первым алгоритмам, совпадают, а третья отличается от них, а именно:
= = (7, 8, 2, 1, 4, 5, 10, 6, 3, 9);
= (7, 8, 2, 6, 1, 4, 5, 10, 3, 9).
Это произошло
потому, что данная задача допускает
наличие нескольких оптимальных
перестановок. Так
как
=
= 5 и 5 меньше значений
и
при i
{1, 4, 5, 10}, то получаем:
min{5, 11} = 5 и min{9,
5} = 5
5 = 5;
min{5, 12} = 5 и min{12,
5 } = 5
5 = 5;
min{5, 10} = 5 и min{13,
5} = 5
5 = 5;
min{5, 6} = 5 и min{15,
5} = 5
5 = 5.
Это означает, что
обслуживание 6-го требования может как
предшествовать, так и не предшествовать
обслуживанию требований 1, 4, 5, 10. В
то же время, хотя
=
=12,
в данной задаче нет такого
значения i,
при котором
пара (
,
)
была бы таковой, что одновременно и
и
были бы меньше 12.
Итак, в результате выполнения задания 2 с помощью трех алгоритмов были получены следующие оптимальные перестановки, две из которых оказались равными, а именно:
= = (7, 8, 2, 1, 4, 5, 10, 6, 3, 9);
= (7, 8, 2, 6, 1, 4, 5, 10, 3, 9).
На основании этих последовательностей можно составить два различных оптимальных расписания для данной задачи, в которых последовательность обслуживания требований будет отличаться, но при этом время окончания обслуживания всех требований будет одно и то же мининальное.
Для наглядности построим графики расписания s0, соответствующего первоначальной последовательности
= (1,
2, 3, 4, 5, 6, 7, 8, 9, 10),
и оптимального расписания s*,
соответствующего первой из найденных
оптимальных последовательностей
=
(7,
8, 2, 1, 4, 5, 10, 6, 3, 9).
Примечание – Для систем обслуживания с одинаковыми маршрутами Flow Shop (к этому типу относится и система обслуживания данной задачи F2| |Cmax) время окончания обслуживания всех требований равно времени окончания обслуживания последнего требования последним прибором согласно заданному маршруту.
Для расписания s0, соответствующего первоначальной последовательности = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10), последним требованием, обслуживаемым прибором В по заданному маршруту
L = (A, B), будет требование с номером 10.
Найдем длительность обслуживания всех требований
по расписанию s0, соответствующего первоначальной последовательности = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10).
Для этого сначала найдем время завершения обслуживания прибором А всех требований для расписания s0, которое будет вычисляться по формулам:
(
)А
= 0+
=
;
(
)А
= (
)А
+
,
для всех
,
где ( )А время завершения обслуживания прибором А требования, обслуживающегося по расписанию s0 i-м в порядке очереди.
Получим:
(
)А
= 0 + 9 = 9;
(
)А
= 9 + 4 = 13;
(
)А
= 13 + 16 = 29;
(
)А
= 29 + 12 = 41;
(
)А
= 41 + 13 = 54;
(
)А
= 54 + 5 = 59;
(
)А
= 59 + 2 = 61;
(
)А
= 61 + 2 = 63;
(
)А
= 63 + 14 = 77;
(
)А
= 77 + 15 = 92.
Теперь найдем время завершения обслуживания прибором В всех требований для расписания s0, которое будет вычисляться по формулам:
(
)В
= (
)А+
;
(
)В
=
,
для всех
,
где ( )В – время завершения обслуживания прибором В требования, обслуживающегося по расписанию s0 i-м в порядке очереди.
Получим:
( )В = 9 + 11 = 20; на 9 единиц времени прибор В начинает работать позже прибора А (9 единиц простоя прибора В);
(
)В
=
;
(
)В
=
29 – 28 = 1 единица простоя;
(
)В
=
41– 33
= 8 единиц простоя;
(
)В
=
54 – 53 =1 единица простоя;
(
)В
=
(
)В
=
(
)В
=
(
)В
=
(
)В
=
.
Так как 9 + 1 + 8 + 1 = 19, следовательно, время общего простоя в работе прибора В для расписания s0 составляет 19 единиц времени.
Найдем время завершения обслуживания обоими
приборами по
маршруту (А,
В) всех
требований для расписания
s0,
соответствующего первоначальной
последовательности
= (1,
2, 3, 4, 5, 6, 7, 8, 9, 10),
т. е. длительность обслуживания
всех требований для расписания s0.
Оно будет
= max
{
i
N
}
= max
{20, 28, 26, 33, 53, 64, 69,
84,
93, 96, 102} =
=
= 102.
Таким образом, время завершения обслуживания всех требований для расписания s0 равно 102 единицам времени, график расписания s0 представлен на рисунке 2.1.
Найдем длительность обслуживания всех требований по расписанию s*, соответствующему первой оптимальной последовательности = (7, 8, 2, 1, 4, 5, 10, 6, 3, 9). Для этого тоже сначала найдем время окончания обслуживания прибором А всех требований для расписания s*, которое будет вычисляться по формулам:
(
*)А
= 0 +
=
;
(
*)А
= (
*)А
+
, для всех
,
где – длительность обслуживания прибором А требования, обслуживающегося по оптимальному расписания s* i-м в порядке очереди;
(
*)А
– время завершения
обслуживания прибором А
требования,
обслуживающегося
по оптимальному расписания s*
i-м
в порядке очереди.
1 2 3 4 5 …
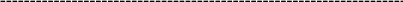В
1 2 3 4 5 6
А
…
0 1 2 3 4 5 6 7 8 9 10 13 15 17 20 25 282930 33 35 4041 44 45 50 53 5455 59
… 5 6 7 8 9 10
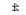В
7 8 9 10
А
596061 636465 6970 75 77 80 848586 90 9293 9596 100 102 t
Рисунок 2.1 – График расписания s0 , соответствующего
первоначальной
последовательности
= (1,
2, 3, 4, 5, 6, 7, 8, 9, 10)
Таким образом, получим:
(
*)А
= (
*)А
= 0 + 2 = 2;
(
*)А
=
(
*)А
= 2 + 2 = 4;
(
*)А
=
(
*)А
= 4 + 4 = 8;
(
*)А
= (
*)А
= 8 + 9 = 17;
(
*)А
=
(
*)А
= 17 + 12 = 29;
(
*)А
= (
*)А
= 29 + 13 = 42;
(
*)А
= (
*)А
= 42 + 15 = 57;
(
*)А
= (
*)А
= 57 + 5 = 62;
(
*)А
= (
*)А
= 62 + 16 = 78;
(
*)А
= (
*)А
= 78 + 14 = 92.
Теперь найдем время завершения обслуживания прибором В всех требований для расписания s*, которое будет вычисляться по формулам:
(
*)В
= (
*)А
+
;
(
*)В
=
,
для всех
,
где
– длительность обслуживания прибором
В
требования, обслуживающегося по
оптимальному расписания s*
i-м
в порядке очереди;
( *)В – время завершения обслуживания прибором В требования, обслуживающегося по оптимальному расписания s* i-м в порядке очереди.
Получим
( *)В = ( *)В = 2+15=17; на 2 единицы времени, прибор В
начинает работать позже прибора А (2 единицы простоя прибора В);
(
*)В
= (
*)В
=
(
*)В
=
(
*)В
=
(
*)В
= (
*)В
=
(
*)В
=
(
*)В
=
(
*)В
= (
*)В
=
(
*)В
= (
*)В
=
(
*)В
=
(
*)В
=
(
*)В
=
(
*)В
=
(
*)В
= (
*)В
=
92 – 82 = 10 единиц простоя.
Так как 2 + 10 = 12, следовательно, время общего простоя
в работе прибора В для оптимального расписания s* составляет
12 единиц времени. Для расписания s* последним требованием, обслуживаемым прибором В по заданному маршруту L = (A, B), будет требование с номером 9.
Найдем время завершения обслуживания обоими приборами по маршруту (А, В) всех требований для оптимального расписания s*, соответствующего первой оптимальной последовательности
= (7, 8, 2, 1, 4, 5, 10, 6, 3, 9), т. е. длительность обслуживания всех требований для расписания s*. Оно будет
=
max{
i
N
}
=
=
max{17,
26, 34, 45, 57, 67, 73, 78, 82, 95}=
=
= 95.
Таким образом, время завершения обслуживания всех требований для расписания s* равно 95 единицам времени, график расписания s* представлен на рисунке 2.2.
В
7 8 2
1 4 5 …
7 8 2 1 4 5 10 6
А
…
0 1 2 3 4 5 6 7 8 9 10 13 15 17 20 2526 282930 3435 40 42 45 50 5455 57 5960 62
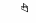… 5 10 6
3 9
В
3 9
А
6263 65 67 70 73 7576 78 80 82 85 90 92 95 100 t
Рисунок 2.2 – График расписания s0 , соответствующего
оптимальной последовательности = (7, 8, 2, 1, 4, 5, 10, 6, 3, 9)
Вывод.
Из графика расписания s0 видно, что если бы
самолеты обеими бригадами готовились к полету в
первоначальной последовательности, т. е. в последовательности
= (1, 2, 3, 4, 5, 6, 7, 8, 9, 10), то на это надо было бы потратить 102 единицы времени. С другой стороны, если самолеты будут готовиться к полету в одной из
найденной оптимальной последовательности, например в последовательности = (7, 8, 2, 1, 4, 5, 10, 6, 3, 9), то на это надо потратить 95 единиц времени, т. е. на 7 единиц времени меньше (102 – 95 = 7).
Таким образом, оптимальное расписание s* эффективнее первоначального расписания s0 на 7 единиц времени. Экономия
по времени достигается благодаря тому, что при подготовке самолетов к полету в оптимальной последовательности уменьшается суммарное время простоев в работе второй бригады (суммарное время простоев в работе второй бригады по расписанию s0 будет
9 + 1 + 8 + 1 = 19). При работе по оптимальному расписанию s* ликвидируются простои в диапазонах 28 – 29, 33 – 41, 53 – 54
с суммарной продолжительностью в 11 единиц времени и уменьшается на 7 единиц времени простой в диапазоне 0 – 9.
При этом получается новый простой в 10 единиц времени в
В
7
8 2 1 4 …
7 8 2 1 4 5 10 6
А
…
0 1 2 3 4 5 6 7 8 9 10 12 14 15 17 20 25 27282930 343536 40 42 4445 50 5455 57 5960 62
… 4 5 10 6 3 9
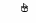В
3 9
А
6263 65 67 70 73 7576 7778 80 8283 85 88 90 92 95 100 t
Рисунок 2.3 –
График улучшенного расписания
,
соответствующего
оптимальной последовательности = (7, 8, 2, 1, 4, 5, 10, 6, 3, 9)
диапазоне 82 – 92, поэтому суммарное время простоев в работе первой бригады будет 12 единиц времени. В итоге получается, что оптимальное расписание s* на 7 единиц времени (19 – 12 = 7) меньше первоначального расписания s0.
Примечание – При необходимости в оптимальном расписании s*
(см. рисунок 2.2) можно убрать простой в 10 единиц, сдвинув вправо по числовой оси начало работы второй бригады на эти 10 единиц, т. е. запланировать работу второй бригады на 10 + 2 = 12 единиц времени позже начала первой. В результате получим еще одно оптимальное расписание , представленное на рисунке 2.3, при котором обе бригады будут работать без простоев.