Перейдем к нормальному усилию в рамках мкр:

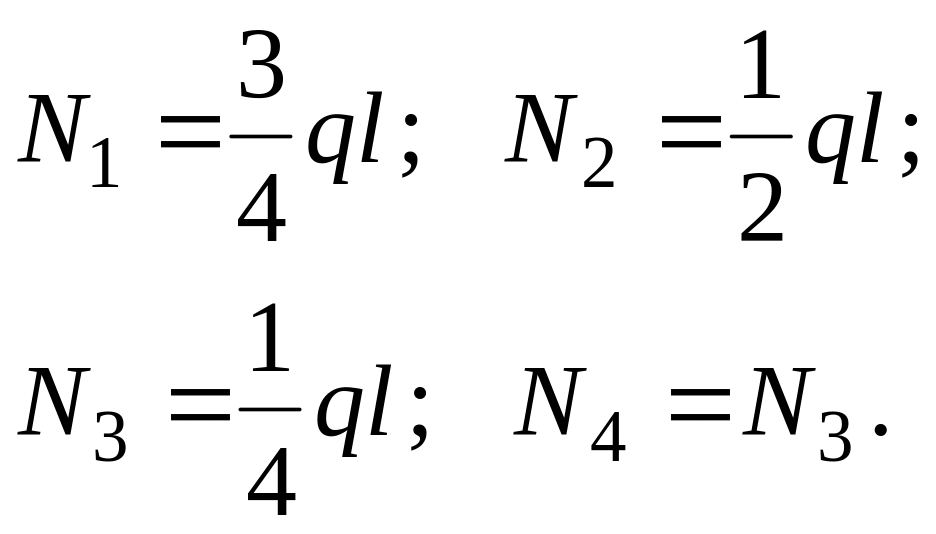
Используем дифференцирующую матрицу:

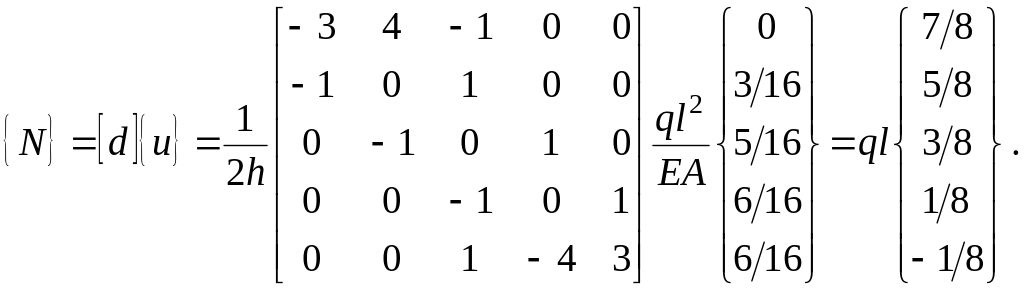
Возьмем пятую законтурную точку.

Система уравнений с учетом граничных условий будет иметь вид:

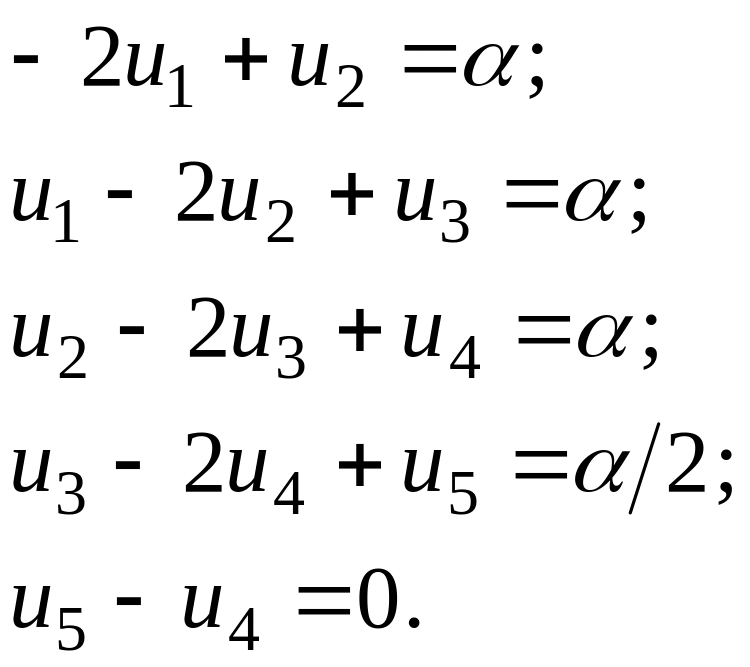
Лекция 3

2.2 Метод Бубнова - Галеркина

В отличие от метода конечных разностей, где использовалась линейная аппроксимация для участков разбиения, в методе Бубнова - Галеркина аппроксимирующая функция записывается для всей области

(24)

где u_i - неизвестные параметры, подлежащие определению; f_i(x_i)- координатная функция, выбираемая таким образом, чтобы она удовлетворяла граничным условиям.

При внесении аппроксимирующей функции в дифференциальное уравнение

(25)

появляется функция невязки , которая по физической сущности представляет собой неуравновешенную нагрузку.

Умножая почленно уравнение (24) на возможное перемещение и интегрируя по области, приходим к соотношению:

(26)

Первое слагаемое представляет собой работу внутренних сил на возможных перемещениях, второе – работу внешних сил, правая часть – работу невязки. Принцип возможных перемещений гласит, что сумма работ внешних и внутренних сил на возможных перемещениях равна нулю. Следовательно, неизвестные параметры находятся из условия равенства нулю работы невязки на возможных перемещениях, то есть

(27)

В нашем случае при геометрических граничных условиях аппроксимирующую функцию можно записать так:

(28)

которая действительно удовлетворяет граничным условиям, так как

В дальнейшем будем удерживать n членов ряда (28). Внесем соотношение (28) в уравнение (5):

(29)

Умножим почленно на и проинтегрируем от 0 до l, положив :

(30)

В силу ортогональности

(31)

Выражение (30) с учетом (31) приобретает вид:

(32)

откуда

(33)

Внося (33) в (28), приходим к выражению для перемещения. Выражение для продольного усилия получается на основании соотношения (4).

(34)

Запишем решение для

Для нормальной силы

(35)

При х=0

(36)

Таблица 6

N	1	2	3	4
	0.129	0.1242	0.1253	0.1249
	0.4053	0.450	0.466	0.475

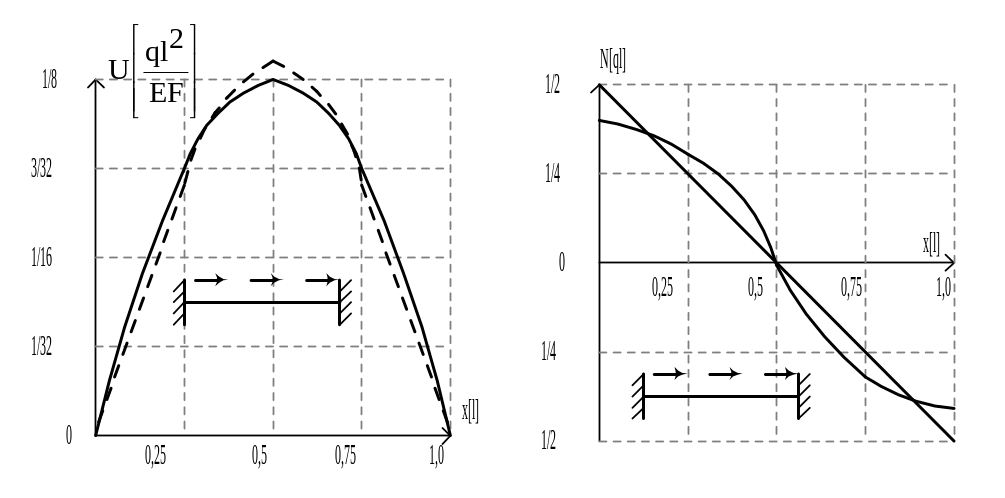
Рисунок 19

Ряд хорошо сходится по перемещениям и плохо – по усилиям.

Лекция 4

2.3 Метод Ритца – Тимошенко

В методе Ритца-Тимошенко неизвестные параметры находятся из условия минимума функционала полной потенциальной энергии, который в случае растяжения-сжатия стержня записывается так:

(37)

Здесь первое и второе слагаемое представляют собой работу внутренних и внешних сил соответственно.

Внося аппроксимирующую функцию (27) в выражение для функционала полной потенциальной энергии, приходим к соотношению:

(38)

Квадрат суммы в первом слагаемом раскрывается так:

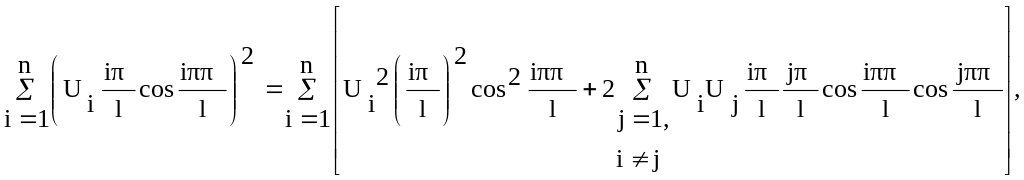
и интеграл от произведения косинусов при равен нулю в силу ортогональности этих функций.

Таким образом

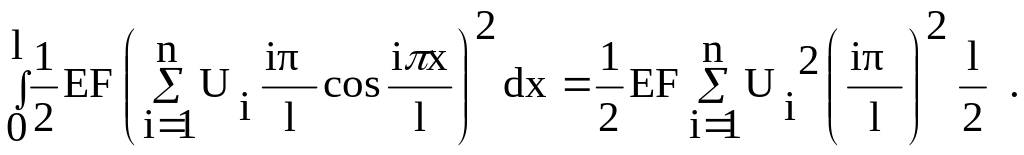
Второй интеграл:

Выражение для полной потенциальной энергии приобретает вид:

(39)

Условие минимума или стационарности функционала

(40)

или в раскрытом виде

(41)

позволяет записать выражение для всех параметров :

(42)

Решение полностью совпадает с решением, полученным методом Бубнова-Галеркина. Следует отметить, что требования к аппроксимирующим функциям в этих методоах различны. В методе Бубнова-Галеркина аппроксимирующая функция должна быть дважды дифференцируемой, а в методе Ритца-Тимошенко – один раз дифференцируемой. Совпадение результатов объясняется тем, что мы использовали в этих методах одну и туж аппроксимитрующую функцию.