ГЛАДКОВ <3

ДВОЙНОЙ ИНТЕГРАЛ

Основные понятия и определения

Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.

Пусть в замкнутой области D плоскости Оху задана непрерывная функция z=ƒ(х;у). Разобьем область D на n «элементарных областей» площади которых обозначим через ΔSi, а диаметры (наи большее расстояние между точками области) - через di(см. рис. 3).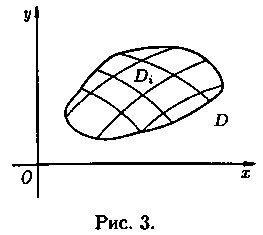

В каждой области Di выберем произвольную точку Mi(xi;yi), умножим значение ƒ(хi;уi) функции в этой точке на ΔSi и составим сумму всех таких произведений:

Эта сумма называется интегральной суммой функции ƒ(х;у) в области D.

Рассмотрим предел интегральной суммы (7.1), когда n стремится к бесконечности таким образом, что maxdi -> 0. Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции ƒ(х;у) по области D и обозначается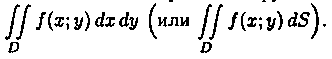

Таким образом, двойной интеграл определяется равенством

В этом случае функция ƒ(х;у) называется интегрируемой в области D; D - область интегрирования; х и у - переменные интегрирования; dxdy (или dS) - элемент площади.

Для всякой ли функции ƒ(х;у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.

Теорема 7.1 (достаточное условие интегрируемости функции). Если функция z=ƒ(х; у) непрерывна в замкнутой области D, то она интегрируема в этой области.

Замечания.

1. Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.

2. Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллель ными координатным осям (см. рис. 4). При этом равенство (7.2) можно записать в виде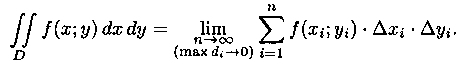

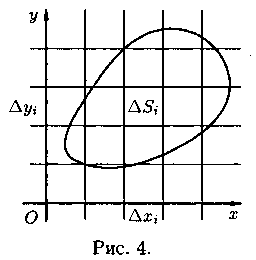
Геометрический и физический смысл двойного интеграла

Рассмотрим две задачи, приводящие к двойному интегралу.

Объем цилиндрического тела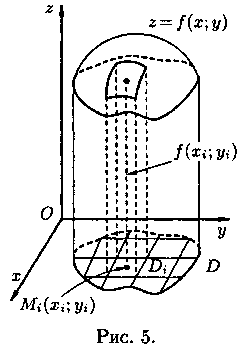

Рассмотрим тело, ограниченное сверху поверхностью снизу - замкнутой областью D плоскости Оху, с боков - цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 5). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z=ƒ(х;у) на плоскость Оху) произвольным образом на п областей Di, площади которых равны Рассмотрим цилиндрические столбики с основаниями Di, ограниченные сверху кусками поверхности z=ƒ(х;у) (на рис. 5 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием Di через ∆Vi, получим

Возьмем на каждой площадке Di произвольную точку Mi(xi;,yi) и заменим каждый столбик прямым цилиндром с тем же основанием D; и высотой zi=ƒ(хi;уi).

Объем этого цилиндра приближенно равен объему ΔVi цилиндрического

столбика, т. е. . Тогда получаем: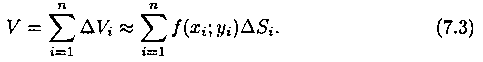

Это равенство тем точнее, чем больше число n и чем меньше размеры «элементарных областей» Di. Естественно принять предел суммы (7.3) при условии, что число площадок Di неограниченно увеличивается (n -> ∞), а каждая площадка стягивается в точку (maxdi-> 0), за объем V цилиндрического тела, т. е.

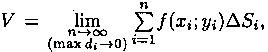
или, согласно равенству (7.2),

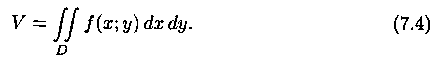
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.