6.2. Максимальные потоки

Среди различных потоков, которые могут быть определены для заданной транспортной сети, особый интерес представляют такие потоки, величина которых является наибольшей.

Определение

Поток  транспортной сети N= (G, c) называется максимальным потоком, если (N) = ,

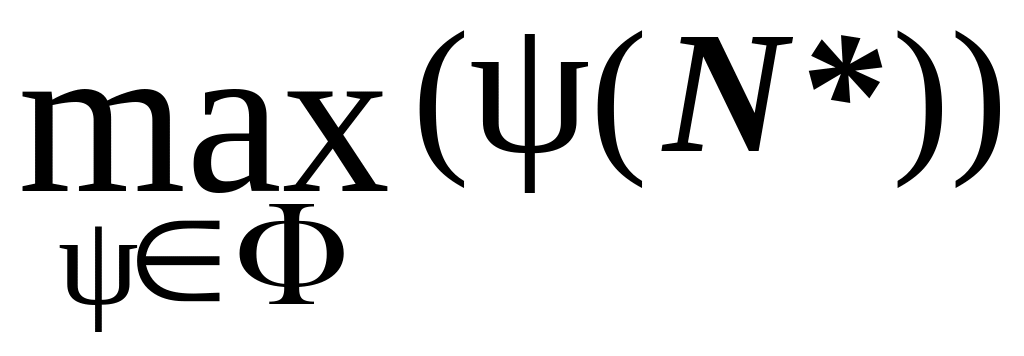где   множество всех потоков в сети N .

Ребро u сети N = (G, c), для которой задан поток , называется полностью нагруженным, если (u) = c(u).

Определение

Поток  транспортной сети N = (G, c) называется полным потоком, если всякий путь в N, ведущий из I в S, содержит хотя бы одно полностью нагруженное ребро.

Упражнение.

1. Показать, что всякий максимальный поток является полным потоком.

2. Привести примеры транспортных сетей, имеющих единственный максимальный поток, несколько разных максимальных потоков. Может ли множество максимальных потоков транспортной сети быть бесконечным?

Напомним, что если W  путь в некотором графе, то E(W) обозначает множество ребер этого пути.

Для построения полного потока в произвольной транспортной сети N = (G, c), где G = (V, U), можно воспользоваться приводимым ниже методом насыщения дуг.

Построение полного потока

1. Образуем нулевой поток ₀, полагая

uU(₀(u) = 0).

2. Преобразуем его в полный поток, повторяя, пока это возможно, следующие действия.

2.1.Пусть определен поток _i.

2.2. В N найдем такой путь W, ведущий из I в S, что

 u  E(W) ( (c (u)  _i (u)) > 0).

2.3. Обозначим как d значение

.

2.4. Переопределим _i в _i+1 по следующей схеме:

_{i + 1} (u) =

Приведенная процедура при каждом выполнении действий 2 делает полностью нагруженным хотя бы одно еще не полностью нагруженное ребро сети. При этом ребра, полностью нагруженные ранее, также остаются полностью нагруженными.

Поэтому приведенная процедура заканчивает свою работу за конечное время. Кроме того, если _i является потоком в сети N, то потоком является и функция _i+1.

Предположим, что заданная процедура заканчивает работу за k шагов. Тогда функция _k образует полный поток в сети N.

Полный поток транспортной сети может быть не максимальным потоком. Например, поток в транспортной сети, приведенной на рис. 6.5, является полным потоком и имеет величину 1.

1(0)

1(0)

1(1) S

I 1(1)

1(0) 1(1)

1(0)

Рис. 6.5

Другой поток в этой же сети, показанные на рис. 6.6, имеет величину 2 и является максимальным.

1(1)

1(1)

1(1) S

I 1(0)

1(1) 1(1)

1(1)

Рис. 6.6

Определение

Множество L  U называется сечением сети N, если для всякого пути W, ведущего из I в S, выполняется условие

 uE(W)(uL).

Если L  сечение транспортной сети N, то после удаления из N ребер множества L сеть распадается на несколько не связанных частей. При этом исток и сток сети попадают в разные части.

Пропускной способностью сечения транспортной сети называется сумма пропускных способностей ребер, входящих в это сечение.

Пропускная способность сечения L обозначается как c(L).

Пропускные способности сечений всякой транспортной сети N и величину произвольного потока  в этой сети связывает следующее соотношение: (N) c(L).

Действительно, суммарный входной поток сети, определяемый как (N) выходит из I и затем передается по вершинам, связанным с S полностью распределяясь по ребрам из L и затем поступает в стока S. Суммарный поток, прошедший по ребрам L не превосходит пропускной способности сечения и в последующем может поступать в сток сети или повторно проходить по ребрам сечения, входящим в состав циклов сети, по которым течет ненулевой поток. Поэтому (N) c(L).

Сечения транспортных сетей обладают следующим важным свойством: величина всякого потока в сети не превосходит пропускную способность любого сечения этой сети.

В частности,  .

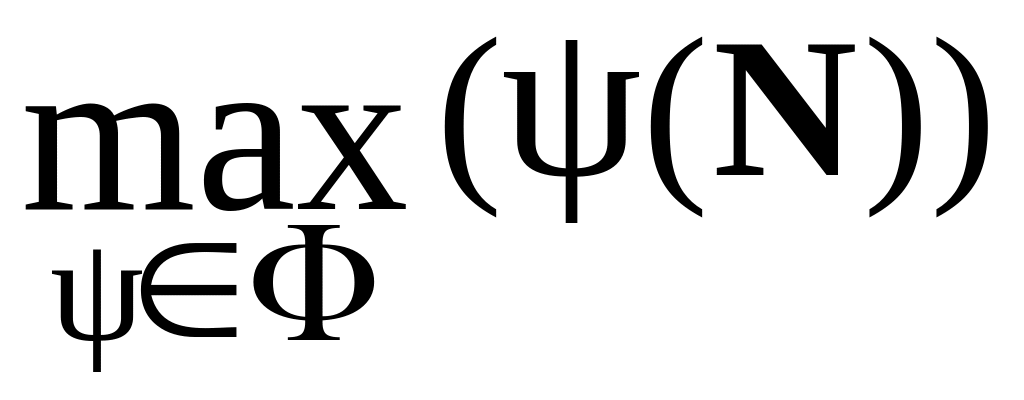
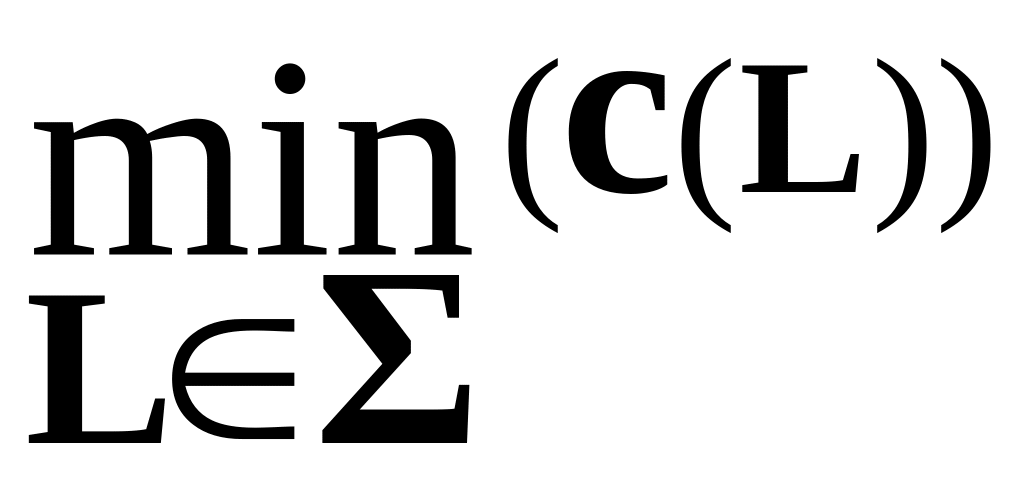Здесь   множество всех сечений сети.

ТЕОРЕМА 6.2

Для всякой транспортной сети N = (G, c) с целочисленной функцией c существует максимальный поток.

Доказательство

Пусть N = ((V, U), c)  некоторая транспортная сеть.

Последовательность Н = x₁, ... , x_k разных вершин этой сети называется цепью, если

i = 1, . . . , k  1 ((x_i, x_i+1)U  (x_i+1, x_i )U).

То есть любые две соседние вершины цепи соединяются между собой ребром одним из двух возможных способов. При этом, если (x_i, x_i+1)U, то такое ребро называется прямым. Если же (x_i+1, x_i)U, то такое ребро называется обратным.

Множество всех прямых и обратных ребер цепи Н обозначается как U(H). Множества прямых и обратных ребер той же цепи обозначаются как U⁺(H) и U^(H) соответственно.

Построим по шагам поток  в транспортной сети N.

1. Положим i = 0 и методом насыщения дуг построим некоторый полный поток _i в сети N.

2. Пока это возможно, повторяем следующие действия.

2.1. Найдем цепь Н = x₁, x₂, . . . , x_{k  1}, x_k, где I = x₁ и S = x_k, для которой выполняются условия:

 u  U⁺(H) (_i(u) < c(u)); (1)

 u  U^(H) (_i(u) > 0). (2)

2.2. Если такая цепь H найдена, то вычислим значения:

d₁ = min(c(u) _i(u)), где u  U⁺(H).

d₂ = min(c(u)), где u  U^(H).

d = min(d₁, d₂).

(Заметим, что d является целым числом и d > 0.)

2.3. Определим функцию _i+1 следующим соотношением:

(u)+d, если u  U⁺(H)

_i+1(u) = (u)d, если u  U^(H)

(u), если u  U(H).

3. Увеличим значение i на 1.

Действие 2 в приведенной процедуре повторяется конечное число раз, поскольку на всяком шаге величина новой функции _i+1 на одном из ребер, ведущих в сток сети, увеличивается на целое число d> 0. Поэтому число повторений выполнения действия 2 не превышает суммы пропускных способностей всех ребер, ведущих в S.

Пусть _k  последняя из функций, определяемых при выполнении приведенной процедуры. Положим  = _k.

Покажем, что  является максимальным потоком в сети N.

1.  является потоком, поскольку если некоторая функция _i  это поток, то действие 2 по потоку _i определяет новый поток _i+1.

Действительно, при определении _i+1 значения потока изменяются только для ребер из U(H). При этом поток в прямых ребрах возрастает, а в обратных убывает на такую величину, что новое значение для каждого ребра сети не превосходит пропускную способность этого ребра и не становится отрицательным. Поэтому для _i+1 выполняется первое условие определения потока в сети.

Для всякой внутренней вершины цепи H сохраняется равенство суммарных входного и выходного потоков.

Действительно, пусть a_j  внутренняя вершина из H.

Рассмотрим возможные случаи прохождения ребер из U(H) через вершину a_j

1. a_j1 a_j a _j+1

При этом входящий и выходящий потоки вершины a_j увеличиваются на d.

2. a_j1 a_j a_j+1

В этом случае входящий поток для вершины a_j по одному входному ребру возрастает на d, а по другому входному ребру убывает на d, а его величина оказывается неизменной, совпадающей с выходным потоком этой вершины.

a_j1 a_j a_j+1

3 .

Входящий и выходящий потоки для a_j уменьшаются на d, оставаясь равными.

a_j1 a_j a_j+1

4 .

Выходящий поток вершины a_j по одному ребру возрастает на d, а по другому ребру убывает на d.

Во всех случаях суммарный входящий поток вершины a_j для _{i+ 1} остается равным суммарному выходящему потоку этой вершины, если такое равенство имеет место для _i. Поэтому для _i+1 выполняется и второе условие определения потока в сети.

2. Покажем, что  является максимальным потоком.

2.1. Обозначим как R  множество таких вершин сети N, что a R тогда и только тогда, когда для всякой цепи H, начинающейся в истоке I и заканчивающейся в a, не выполняются условия

 u U⁺(H) (_i(u) < c(u)) (1)

 u U^(H) (_i(u) > 0) (2)

Множество R является непустым, так как из определения функции  следует, что S  R.

Множество остальных вершин сети обозначим F. Так как для I выполнены условия (1) и (2). Действительно, единственная цепь, ведущая из I в I, состоит из вершины I. Для этой цепи выполняются условия (1) и (2).Значит I F и F не является пустым множеством.

2.2. Обозначим как L множество ребер сети N, начала которых принадлежат множеству F, а концы  множеству R.

Всякий путь W из I в S содержит хотя бы одно ребро из L, поскольку его начало лежит в F, а конец  в R. Следовательно, в последовательности W содержатся две последовательно идущие вершины a и b, для которых aF и bR. Поэтому L образует сечение сети N.

2.3. Все ребер сечения L справедливо свойство:

uL ((u) = c(u)).

То есть все ребра L полностью нагружены потоком. В противном случае, если ребро u= (a,b),является недогруженным, то вершина b такого ребра из L, не может принадлежать R.

Действительно, если (u)  c(u), то найдется цепь, ведущая в b, которая проходит через u, в которой все прямые ребра недогружены, а по обратным ребрам течет ненулевой поток. Такая цепь может быть получена добавлением вершины b к цепи, ведущей в a, для которой выполнены условия (1) и (2). Последнее ребро для такой цепи является прямым и оно недогружено.Поэтому bF, а это противоречит предположению, что bR.

2.4. Если u = (a, b)  это ребро, для которого a R и b F, то (u) = 0.

Чтобы убедиться в справедливости последнего свойства, предположим противное: существует такое ребро u = (a, b), что a R, b F и (u) > 0.

Тогда, так как b F, то существует цепь H = I, . . . , b, для которой выполнены условия (1) и (2). Но тогда эти же условия выполнены и для цепи H^* = I, ... , b, a. Поскольку в ней вершины a и b связаны обратным ребром, по которому течет ненулевой поток.

Поэтому a F, что противоречит предположению о том, что a R.

Следовательно, поток между вершинами множеств F и R может протекать лишь в одном направлении.

2.5. Поэтому суммарный поток, проходящий через ребра сечения L, в дальнейшем распространяется только между вершинами множества R и полностью входит в сток S.

Следовательно, справедливо соотношение (N) = c (L).

То есть   это максимальный поток, так как его величина совпадает с пропускной способностью сечения L, величину которого не превосходит ни один поток в сети.

Доказательство окончено.

СЛЕДСТВИЕ 1

Для всякой транспортной сети величина максимального потока равна минимуму пропускных способностей сечений этой сети.

СЛЕДСТВИЕ 2

Пусть N = (G, c)  транспортная сеть с функцией пропускной способности, принимающей рациональные значения.

Тогда для N существует максимальный поток.

Доказательство

Пусть рациональные значения пропускных способностей ребер u₁, ... , u_m транспортной сети N = (G, c) задаются как отношения неотрицательных целых чисел p₁/q₁ , . . . , p_m/q_m.

Пусть d = q₁  ...  q_m.

Рассмотрим сеть N^* = (G, c^*), для которой c^* = dc. Поскольку функция c^* принимает только целочисленные значения, то для N^* существует максимальный поток ^*.

Тогда поток  = ^*\ d является максимальным потоком для транспортной сети N.

Действительно, сечение L для G, пропускная способность которого в сети N ^*совпадает с величиной потока ^*, в сети N имеет пропускную способность, совпадающую с величиной потока . Поэтому   это максимальный поток.

Доказательство окончено.

ТЕОРЕМА 6.3

Для всякой транспортной сети существует максимальный поток.

Доказательство

Пусть N = (G, c)  это произвольная транспортная сеть. Рассмотрим последовательность рациональнозначных функций пропускной способности ребер сети N: c₁, . . . , c_i, . . . , которые равномерно сходятся к функции c снизу.

Из следствия 2 следует, что для транспортных сетей N_i = (G, c_i), i = 1, ... существуют максимальные потоки

₁, . . . , _i, . . . (1)

Пусть сеть N содержит ребра u₁, ... , u_m.

Из последовательности (1) выделим такую бесконечную подпоследовательность потоков

_1,1 . . . , _1,j, . . . (2),

что числовая последовательность ₁,_i(u₁), i = 1, 2, . . . является сходящейся.

Из последовательности (2) выделим подпоследовательность

₂,₁, . . . , ₂,_j . . . (3).

Для (3) числовая последовательность ₂,_j (u₂), j = 1, 2, . . .также является сходящейся.

Продолжая процесс выделения подпоследовательностей, через конечное число шагов получаем последовательность функций

_m,₁, ... , _m,_j, . . . (m).

Эта последовательность состоит из потоков, значения которых на каждом ребре сети образуют сходящиеся последовательности.

Пусть  .

1. Покажем, что  является потоком.

Поскольку для всякого потока _m,_j справедливо неравенство

_m,_j c_m,j, то c.

Кроме того, для всякого потока _m,_j и внутренней вершины a сети N_m,_j выполняется равенство

.

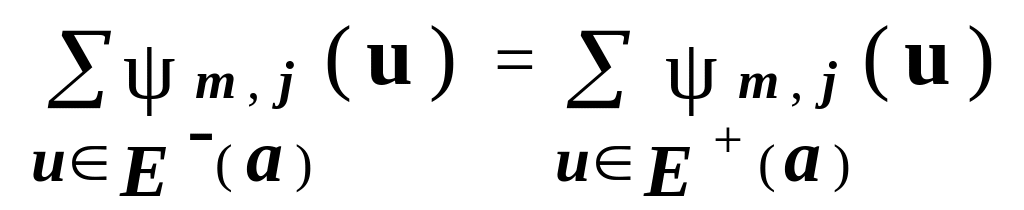Предельный переход по j   преобразует последнее равенство в равенство

.

Следовательно,  является потоком в N.

2. Покажем, что   это максимальный поток.

Если c_m,_j  функция пропускной способности, отличающаяся от c на всех ребрах сети не более чем на , то величина всякого потока в транспортной сети N не превосходит величины  + k  , где k  число ребер, выходящих из истока сети.

Поскольку значение  можно выбрать сколь угодно малым, то величина всякого потока в N не превосходит значения величины потока . Следовательно,   это максимальный поток.

Доказательство окончено.

177