
- •Вопрос 32: Формулы Тейлора для основных элементарных функций (тригонометрические функции)
- •Вопрос 33: Монотонные функции. Достаточные условия монотонности.
- •Вопрос 34: Локальные экстремумы. Исследование функции на экстремум. Необходимые, достаточные условия экстремума.
- •Вопрос 35: Исследование функций на экстремум. Достаточные условия. Примеры.
Вопрос 35: Исследование функций на экстремум. Достаточные условия. Примеры.
Точку называют точкой максимума функции y = f(x), если для всех x из ее окрестности
справедливо
неравенство
![]() .
Значение функции в точке максимума
называют максимумом
функции
и обозначают
.
Значение функции в точке максимума
называют максимумом
функции
и обозначают
![]() .
Точку
называют
точкой
минимума
функции y
= f(x),
если для всех x из ее окрестности
справедливо неравенство
.
Точку
называют
точкой
минимума
функции y
= f(x),
если для всех x из ее окрестности
справедливо неравенство
![]() .
Значение функции в точке минимума
называют минимумом
функции
и обозначают
.
Значение функции в точке минимума
называют минимумом
функции
и обозначают
![]() .
Под
окрестностью точки
понимают
интервал
.
Под
окрестностью точки
понимают
интервал
![]() ,
где
-
достаточно малое положительное
число.
Точки минимума и максимума
называют точками
экстремума,
а значения функции, соответствующие
точкам экстремума, называют экстремумами
функции.
,
где
-
достаточно малое положительное
число.
Точки минимума и максимума
называют точками
экстремума,
а значения функции, соответствующие
точкам экстремума, называют экстремумами
функции.
Достаточные признаки экстремума функции.
Для нахождения максимумов и минимумов функции можно пользоваться любым из трех достаточных признаков экстремума. Хотя самым распространенным и удобным является первый из них. Первое достаточное условие экстремума.
Пусть функция y = f(x) дифференцируема в -окрестности точки , а в самой точке непрерывна. Тогда
если при и при , то - точка максимума;
если при и при , то - точка минимума.
Другими словами:
-если в точке функция непрерывна и в ней производная меняет знак с плюса на минус, то - точка максимума;
-если в точке функция непрерывна и в ней производная меняет знак с минуса на плюс, то - точка минимума.
Алгоритм.
-Находим область определения функции.
-Находим производную функции на области определения.
-Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (эти точки называют точками возможного экстремума, проходя через эти точки, производная как раз может изменять свой знак).
-Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).
-Выбираем
точки, в которых функция непрерывна и,
проходя через которые, производная
меняет знак.
Пример.
Найти
экстремумы функции
![]() .
Решение.
Областью
определения функции является все
множество действительных чисел, кроме
x
= 2.
Находим
производную:
.
Решение.
Областью
определения функции является все
множество действительных чисел, кроме
x
= 2.
Находим
производную:
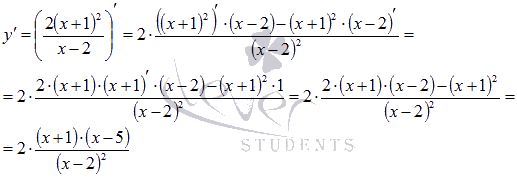 Нулями
числителя являются точки x
= -1
и x
= 5,
знаменатель обращается в ноль при x
= 2.
Отмечаем эти точки на числовой
оси
Нулями
числителя являются точки x
= -1
и x
= 5,
знаменатель обращается в ноль при x
= 2.
Отмечаем эти точки на числовой
оси
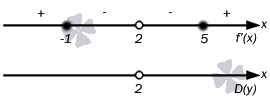 Определяем
знаки производной на каждом интервале,
для этого вычислим значение производной
в любой из точек каждого интервала,
например, в точках x
= -2, x = 0, x = 3
и x
= 6.
Определяем
знаки производной на каждом интервале,
для этого вычислим значение производной
в любой из точек каждого интервала,
например, в точках x
= -2, x = 0, x = 3
и x
= 6.
 ,
следовательно, на интервале
,
следовательно, на интервале
![]() производная
положительна (на рисунке ставим знак
плюс над этим интервалом).
Аналогично
производная
положительна (на рисунке ставим знак
плюс над этим интервалом).
Аналогично
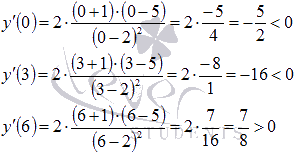 Поэтому
над вторым интервалом ставим минус, над
третьим – минус, над четвертым –
плюс.
Осталось выбрать точки, в
которых функция непрерывна и ее
производная меняет знак. Это и есть
точки экстремума.
В точке x
= -1
функция непрерывна и производная меняет
знак с плюса на минус, следовательно,
по первому признаку экстремума, x
= -1
– точка максимума, ей соответствуем
максимум функции
Поэтому
над вторым интервалом ставим минус, над
третьим – минус, над четвертым –
плюс.
Осталось выбрать точки, в
которых функция непрерывна и ее
производная меняет знак. Это и есть
точки экстремума.
В точке x
= -1
функция непрерывна и производная меняет
знак с плюса на минус, следовательно,
по первому признаку экстремума, x
= -1
– точка максимума, ей соответствуем
максимум функции
 .
В
точке x
= 5
функция непрерывна и производная меняет
знак с минуса на плюс, следовательно, x
= -1
– точка минимума, ей соответствуем
минимум функции
.
В
точке x
= 5
функция непрерывна и производная меняет
знак с минуса на плюс, следовательно, x
= -1
– точка минимума, ей соответствуем
минимум функции
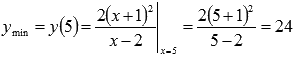 .
Графическая
иллюстрация.
.
Графическая
иллюстрация.
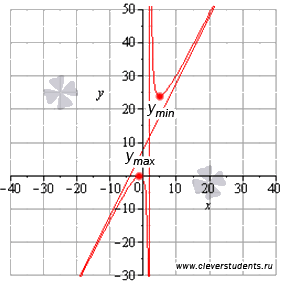 Ответ:
Ответ:
![]() .
ОБРАТИТЕ
ВНИМАНИЕ: первый достаточный признак
экстремума не требует дифференцируемости
функции в самой точке
.
Второй
достаточный признак экстремума
функции.
Пусть
.
ОБРАТИТЕ
ВНИМАНИЕ: первый достаточный признак
экстремума не требует дифференцируемости
функции в самой точке
.
Второй
достаточный признак экстремума
функции.
Пусть
![]() ,
,
если
![]() ,
то
-
точка минимума;
,
то
-
точка минимума;
если
![]() ,
то
-
точка максимума.
,
то
-
точка максимума.
Как
видите, этот признак требует существования
производной как минимум до второго
порядка в точке
.
Пример.
Найти
экстремумы функции
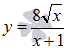 .
Решение.
Начнем
с области определения:
.
Решение.
Начнем
с области определения:
 Продифференцируем
исходную функцию:
Продифференцируем
исходную функцию:
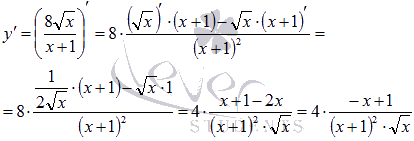 Производная
обращается в ноль при x
= 1,
то есть, это точка возможного
экстремума.
Находим вторую
производную функции и вычисляем ее
значение при x
= 1:
Производная
обращается в ноль при x
= 1,
то есть, это точка возможного
экстремума.
Находим вторую
производную функции и вычисляем ее
значение при x
= 1:
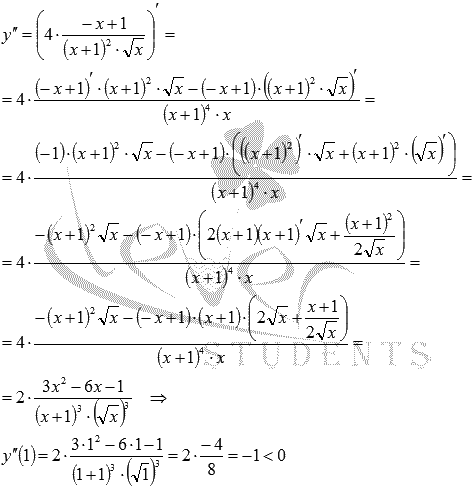 Следовательно,
по второму достаточному условию
экстремума, x
= 1
- точка максимума. Тогда
Следовательно,
по второму достаточному условию
экстремума, x
= 1
- точка максимума. Тогда
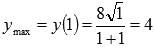 -
максимум функции.
Графическая
иллюстрация.
-
максимум функции.
Графическая
иллюстрация.
 Ответ:
Ответ:
![]() .
Третий
достаточный признак экстремума
функции.
Пусть
функция y
= f(x)
имеет производные до n-ого
порядка в
-окрестности
точки
и
производные до n+1-ого
порядка в самой точке
.
Пусть
.
Третий
достаточный признак экстремума
функции.
Пусть
функция y
= f(x)
имеет производные до n-ого
порядка в
-окрестности
точки
и
производные до n+1-ого
порядка в самой точке
.
Пусть
![]() и
и
![]() .
Тогда,
.
Тогда,
если n – четное, то - точка перегиба;
если n – нечетное, то - точка экстремума.
Причем,
если
![]() ,
то
-
точка минимума;
,
то
-
точка минимума;
если
![]() ,
то
-
точка максимума.
,
то
-
точка максимума.
Пример.
Найти
точки экстремума функции
![]() .
Решение.
Исходная
функция является целой рациональной,
ее областью определения является все
множество действительных
чисел.
Продифференцируем
функцию:
.
Решение.
Исходная
функция является целой рациональной,
ее областью определения является все
множество действительных
чисел.
Продифференцируем
функцию:
 Производная
обращается в ноль при
Производная
обращается в ноль при
![]() ,
следовательно, это точки возможного
экстремума. Воспользуемся третьим
достаточным признаком экстремума.
Находим
вторую производную и вычисляем ее
значение в точках возможного экстремума
(промежуточные вычисления
опустим):
,
следовательно, это точки возможного
экстремума. Воспользуемся третьим
достаточным признаком экстремума.
Находим
вторую производную и вычисляем ее
значение в точках возможного экстремума
(промежуточные вычисления
опустим):
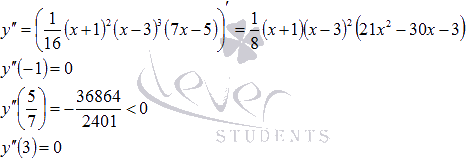 Следовательно,
Следовательно,
![]() -
точка максимума (для третьего достаточного
признака экстремума имеем n
= 1
и
-
точка максимума (для третьего достаточного
признака экстремума имеем n
= 1
и
![]() ).
Для
выяснения характера точек
).
Для
выяснения характера точек
![]() находим
третью производную и вычисляем ее
значение в этих точках:
находим
третью производную и вычисляем ее
значение в этих точках:
 Следовательно,
Следовательно,
![]() -
точка перегиба функции (n
= 2
и
-
точка перегиба функции (n
= 2
и
![]() ).
Осталось
разобраться с точкой
).
Осталось
разобраться с точкой
![]() .
Находим четвертую производную и вычисляем
ее значение в этой точке:
.
Находим четвертую производную и вычисляем
ее значение в этой точке:
 Следовательно,
-
точка минимума функции.
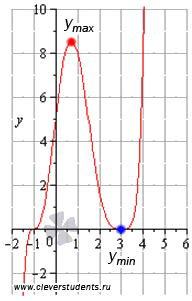
Графическая
иллюстрация.
Следовательно,
-
точка минимума функции.
Графическая
иллюстрация.
 Ответ:
- точка максимума,
-
точка минимума функции.
Ответ:
- точка максимума,
-
точка минимума функции.
