42. Корреляция и регрессия.

Часто наблюдаемые величины находятся в более сложных зависимостях, чем функциональная. Подобного рода зависимости относят к корреляционным зависимостям.

Определение. Две случайные величины X и Y находятся в корреляционной зависимости, если каждому значению любой из этих величин соответствует определенное распределение вероятностей другой величины.

Определение. Условным математическим ожиданием дискретной случайной величины X при Y = y (y –определенное возможное значение Y) называют сумму произведений возможных значений X на их условные вероятности:

(1),

где - условная вероятность равенства при условии, что Y = y.

Для непрерывных величин , где - плотность вероятности случайной непрерывной величины X при условии Y = y.

Условное математическое ожидание есть функция от y: , которую называют функцией регрессии величины X на величину Y.

Уравнение называют уравнением регрессии X на Y, а линию на плоскости, соответствующую этому уравнению, называют линией регрессии.

Уравнение регрессии Y на X записывается в виде функции .

Определение. Если X и Y – независимые случайные величины, то

(2)

Если X и Y – не являются независимыми случайными величинами, то, вообще говоря, .

За меру зависимости двух случайных величин X и Y принимают безразмерную величину , определяемую соотношением

(3)

или более кратко соотношением (4), где , , , и называемую коэффициентом корреляции.

Определение. Случайные величины X и Y называют некоррелированными, если r = 0, и коррелированными, если .

Свойства коэффициента корреляции:

1. Если X и Y – независимые случайные величины, то коэффициент корреляции равен 0. Обратное утверждение неверно.

2. Если 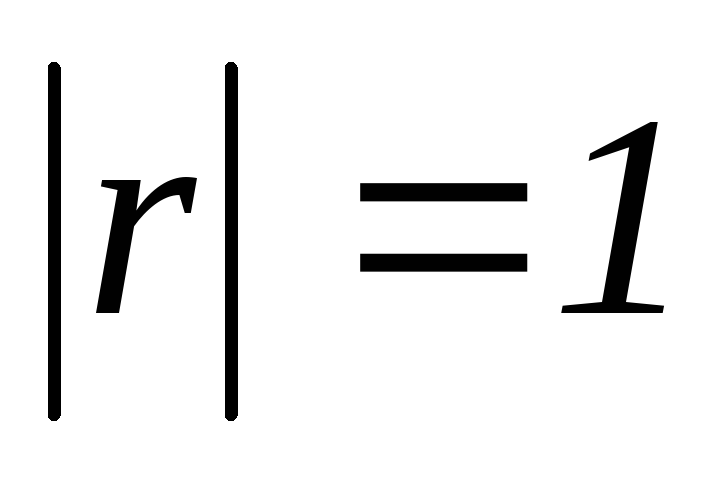, то между случайными величинами X и Y имеет место функциональная, а именно линейная, зависимость.

3. Коэффициент корреляции характеризует относительную величину отклонения математического ожидания произведения от произведения математических ожиданий 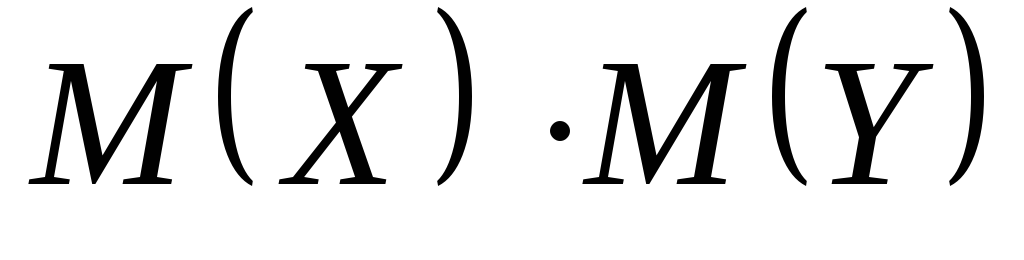, поэтому можно утверждать, что он характеризует тесноту зависимости между X и Y.

Прямые регрессии.

Определение. Корреляционная зависимость между случайными величинами X и Y называется линейной корреляцией, если обе функции регрессии и являются линейными. В этом случае обе линии регрессии являются прямыми; они называются прямыми регрессии.

Коэффициент называют коэффициентом регрессии Y на X и обозначают

(5).

Соответственно уравнение прямой регрессии Y на X имеет вид: .

С учетом коэффициента корреляции уравнения прямых регрессии можно записать в виде:

, (6).

Коэффициенты корреляции связаны с коэффициентами регрессии отношением:

(7).

43. Задача линейного программирования. Основные составляющие.

Под задачей линейного программирования будем понимать следующую задачу.

Даны система m линейных ограничений с n неизвестными (система может содержать как уравнения, так и неравенства того или иного знака).

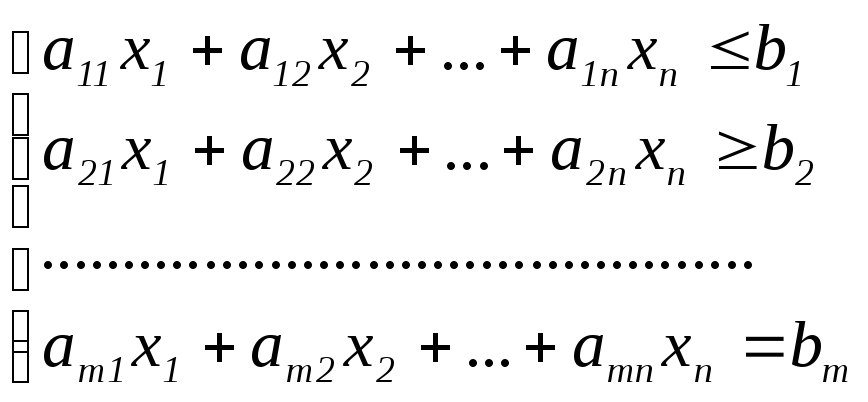(1)

Условие неотрицательности неизвестных:

, , …, (2)

Целевая линейная функция, зависящая от n неизвестных:

. (3)

- вектор неизвестных.

Требуется найти такой план системы линейных ограничений (1), при котором целевая функция (3) примет наибольшее или наименьшее значение, т.е. найти оптимальный план задачи.

Планом задачи (1)-(3) называется всякое неотрицательное решение системы линейных ограничений (1), то есть план – это вектор , удовлетворяющий условиям (1) и (2).

План называется оптимальным планом задачи максимизации (минимизации), если

,

где X – любой план задачи.

Решить задачу ЛП – это значит найти ее оптимальный план и подсчитать максимальное (минимальное) значение целевой функции.

При решении задачи ЛП возможны следующие случаи:

1. Существует оптимальный план (единственный или бесконечное множество оптимальных планов).

2. Оптимального плана не существует, так как планы в задаче есть, но на непустом множестве планов целевая функция не ограничена (сверху – в задаче максимизации или снизу – в задаче минимизации).

3. Оптимального плана не существует, так как в задаче вообще нет ни одного плана.

Будем рассматривать три формы задачи линейного программирования, а именно:

1. общая задача,

2. основная задача,

3. каноническая задача.

Задачу ЛП будем называть общей задачей, если система линейных ограничений (1) содержит хотя бы одно неравенство, и основной задачей, если все ограничения системы (1) являются уравнениями.

Задачу ЛП будем называть канонической задачей, если она является частным случаем основной задачи в том смысле, что система линейных уравнений – каноническая, а целевая функция выражена только через свободные неизвестные.

Система линейных уравнений называется канонической системой, если она удовлетворяет двум условиям:

1. в каждом уравнении содержится неизвестное с коэффициентом, равным единице, отсутствующее во всех остальных уравнениях и называемое базисным неизвестным,

2. свободные члены всех уравнений неотрицательны.

Неизвестные, не являющиеся базисными, называются свободными неизвестными. При m = 2, n = 4, если предполагать базисными неизвестные и , каноническую задачу можно записать в виде

(4)

, (5)

(min) (6)

Если в канонической системе положить все свободные неизвестные равными нулю, то базисные неизвестные будут равны неотрицательным свободным членам уравнений. Полученный таким способом план называется базисным планом канонической задачи. При из системы (4) получим, что , и базисный план задачи (4)-(6) будет иметь вид

,

причем, как видно из выражения (6), значение целевой функции для этого плана .

Из трех форм задачи ЛП главная роль отводится канонической, так как алгоритм, например, симплекс-метода непосредственно применяется к канонической задаче, а общая и основная задачи, в конечном счете, сводятся к канонической.

Для того, чтобы общую задачу привести к основной, то есть неравенства заменить уравнениями, достаточно вести неотрицательные дополнительные неизвестные, прибавив их к левым частям неравенств «типа », вычтя из левых частей неравенств «типа » и приписав к заданной целевой функции с нулевыми коэффициентами. Основная задача сводится к одной или двум каноническим, решаемым непосредственно одна за другой, с помощью метода искусственного базиса.