Многошаговые методы1

Многошаговые методы. Метод Адамса.

Если дифференциальное уравнение у'=f(х, у) име­­ет в правой части сложное ана­ли­ти­чес­кое вы­ра­же­ние, значение которого быстро изменяется при незначительном изменении аргумента, то рассмотренные выше одношаговые методы не дают желаемую точность вычислений. В таких случаях применяют многошаговые методы решения ДУ. К таким методам относятся экст­ра­по­ля­ционный и интерполяционный методы Адамса.

Экстраполяционный метод Адамса.

Пусть для дифференциального уравнения у'=f(х, у) зада­ны на­­чаль­ные условия х=х₀ , у=у_{0, а также известны или определены с помощью одношаговых методов ещё m точек искомой функции} у_1, у_{2, …} у_m. Требуется най­ти ре­ше­­ние уравнения у'=f(х, у) на отрезке [а, b].

Разобьем отрезок [а, b] равномерно на n частей точ­ка­­­ми х_i=х₀+ h^.i, i=0, 1,...,n, h = (b - а)/n. Выберем про­­из­воль­но элементарный отрезок, на котором про­ин­тегрируем диф­ференциальное уравнение

_или

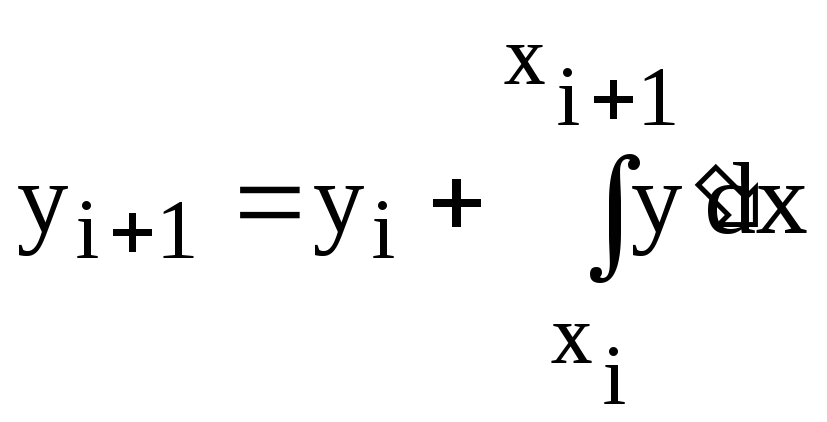
Если обозначить

,

то рекуррентная формула метода примет вид

у_i+1=у_i+у_i.

Для нахождения производной воспользуемся вто­рой ин­терполяционной формулой Ньютона. С учётом t= (х - х_i)/h получим:

Подставим полученное выражение для у' в ин­те­­граль­ное уравнение и, учитывая, что dх = hdt, име­ем

где

Обозначим через q_i=у_i' h=f(х_i, у_i)^.h, , тог­да для любой разности ^mq_i=^m (у_i'h) имеем вы­ражение

y_i =q_i+1/2 ^.q_i-1+5/12 ^.²q_i-2+3/8 ^.³q_i-3+…+Сm^.^mq_i-m+…,

используемое для получения решения урав­нения

у_i+1= у_i+у_i.

Две по­­след­ние формулы яв­ля­ют­ся основными в эк­стра­по­ля­ци­он­ном методе Адам­са.

Погрешность экстраполяционного метода Адамса можно оценить по формуле

,

где .

Для метода Адамса характерно убывание абсолютных величин конечных разностей. Этим обстоятельством обусловлен выбор m и h. Чем меньше h, тем ниже будет m – порядок конечных разностей. Однако это приводит к увеличению узловых точек, а значит и применению укороченных формул, что в свою очередь связано с ростом погрешности вычислений. Обычно m и h стараются подобрать так, чтобы последняя конечная разность, участвующая в вычислениях была практически постоянной. Обрывать формулу на практически постоянной разности удобно ещё из тех соображений, что это обстоятельство может быть использовано для текущего контроля вычислений.

Чаще всего применяется эк­стра­по­ля­ци­он­ный метод Адамса ограниченный тремя конечными разностями.

у_i+1 = у_i + q_i+1/2 ^.q_i-1+5/12 ^.²q_i-2+3/8 ^.³q_i-3

Для начала процесса вычисления нужны четыре на­чаль­ных значения у₀, у₁, у₂ и у_3, которые мож­но опре­де­лить любым известным методом. Далее, зная у₀, у₁, у₂ и у₃ , находят q₀=hy₀=h f(x₀, y₀); q₂= hy₂ =h f(x₂, y₂); q₃ = hy₃=h f(x₃, y₃); q₄= hy₄= hf(x₄, y₄) и составляют таблицу конечных раз­нос­тей ве­личин q (табл.)

Таблица 4.3

№ п/п	xi	yi	yi	yi’=f(x0,y0)	qi = hyi’	Конечные разности
0	x0	y0		f(x0,y0)	—	—	—	—
1	x1	y1		f(x1,y1)	q0	q0	2q0	3q0
2	x2	y2		f(x2,y2)	q1	q1	2q1
3	x3	y3	y3	f(x3,y3)	q2	q2
4	x4	y4		f(x4,y4)	q3
5	x4	y5		...	...
...	...	...

Метод Адамса заключается в продолжении дан­ной таб­ли­цы разностей с помощью формулы для у_i. Ис­поль­зуя уже вычисленные q₃, q₂, ^q₁ и ^q₀, рас­по­ло­жен­ные в таб­­лице диагонально, по формуле для у_i по­лу­чают, по­ла­гая n = 3,

у₃ = q₃ + 0.5q₂ + (5/12) ^. ^q₁ + (3/8) ^. ^q₀ ,

у₃ вносят в таблицу и находят у₄ = у₃+у₃. Затем, ис­поль­зуя х₄ и у₄ находят f(х₄,у₄), q₄, q₃, ^q₂ и ^q₁, т.е. новую ди­­а­го­наль. По этим данным опре­деляют значение у₄, ко­то­рое тут же вно­сят в таб­ли­цу, и находят у₅ = у₄ + у₄.

Таблицу продолжают по описанному алгоритму до ее за­пол­­не­ния, вычисляя правую часть формулы при этом толь­ко один раз. Что­бы оценить погрешность по­лу­­чен­но­го результата, можно применить правило Рун­­ге или просто следить за третьими разностями ^q_i, ко­то­рые считаются по­сто­ян­ны­ми. Этого мож­но добиться, вы­­бирая h каждый раз та­кой, что­­бы выражение для оценки погрешности бы­ло |³q_i-1 - ³q_i| < . На практике h выбирают из не­ра­вен­ст­ва h⁴ < , где - за­данная точность ре­ше­ния.

Метод Рунге состоит в том, что сначала находится ре­шение диф­фе­рен­ци­аль­но­го уравнения при шаге h, а за­тем зна­че­ние h удва­и­ва­ет­ся и находится решение при но­­вом шаге. Погрешность оце­нивается по формуле

= (2^m - 1) ^. |y_n^~ - y^~_2n| ,

где y_n^~ - значение приближенного вычисления при двойном шаге; m - порядок метода.

Интерполяционный метод Адамса (уточняющая формула).

Алгоритм интерполяционного метода Адамса можно представить в виде

где ;

.

Для применения интерполяционной формулы Адамса на начальном этапе необходимо знать приближённое значение функции в точке x_i+1. Для этого можно использовать экстраполяционную формулу Адамса. Тогда интерполяционная формула Адамса служит, как уточняющая в методе Адамса.

На практике поступают следующим образом:

1. по экстрополяционной формуле Адамса вычисляют y_i+1;

2. затем это значение уточняют с помощью интерполяционной формулы;

3. если , то в качестве уточнённого решения принимается 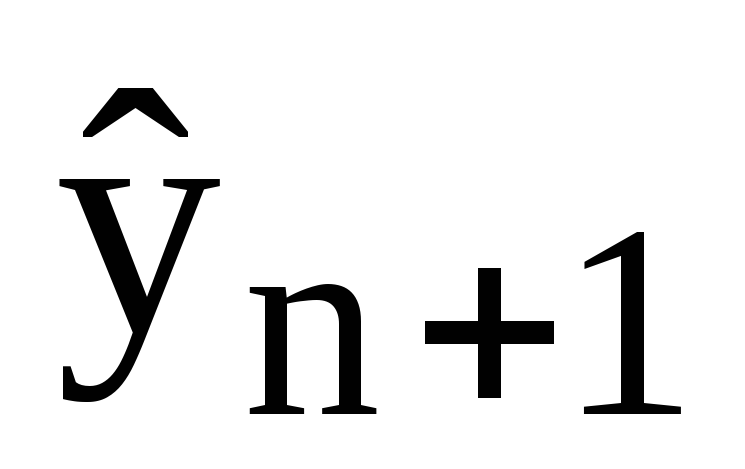, иначе производится уточнение для по интерполяционной формуле Адамса.