
11072
.pdf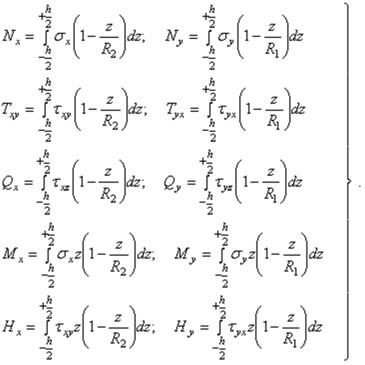
(2.1)
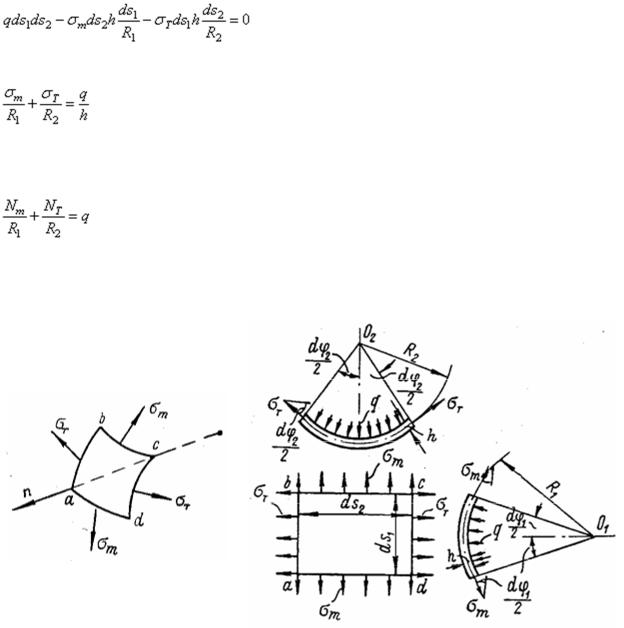
При переходе от одной грани выделенного элемента к соседней, расположенной на расстоянии dS1 или dS2 (рис. 39,а) от первой, необходимо учитывать приращение усилий.
Вследствие того, что трапеции, образующие боковые грани элемента, различны, сдвигающие силы Тxу и Туx не равны между собой, несмотря на справедливость закона
парности 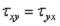 касательных напряжений. Однако обычно толщина h, а, следовательно, и расстояние z малы по сравнению с радиусами R1 и R2, поэтому отношения
касательных напряжений. Однако обычно толщина h, а, следовательно, и расстояние z малы по сравнению с радиусами R1 и R2, поэтому отношения  и
и 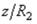 малы по сравнению с единицей и могут быть сразу отброшены. Тогда
малы по сравнению с единицей и могут быть сразу отброшены. Тогда
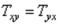 ,
,
т. е. закон парности сдвигающих усилий становится действительным.
Для решения статически неопределимой задачи о напряженном состоянии можно составить следующие уравнения:
1.Пять дифференциальных уравнений равновесия, представляющих собой суммы проекций всех сил, действующих на элемент, на оси Ох, Оу и Оz и суммы моментов этих сил относительно осей Ох и Оу. Уравнение равновесия в виде суммы моментов всех сил относительно оси Оz превращается в тождество 0 = 0 на основании закона парности касательных напряжений.
2.Три геометрических дифференциальных уравнения, связывающих относительные
деформации 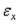 ,
, 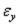 и
и 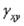 с составляющими перемещениями u0, v0 и w0 срединной поверхности, и три геометрических дифференциальных уравнения, связывающих вели-
с составляющими перемещениями u0, v0 и w0 срединной поверхности, и три геометрических дифференциальных уравнения, связывающих вели-
чины κx и κy, характеризующие изменения кривизн срединной поверхности, и величину 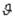 , характеризующую ее кручение, с составляющими u0, v0 и W0. Появление перемещений
, характеризующую ее кручение, с составляющими u0, v0 и W0. Появление перемещений
κx, κy и 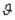 связано с тем, что элемент оболочки под нагрузкой получает дополнительное искривление.
связано с тем, что элемент оболочки под нагрузкой получает дополнительное искривление.
3. Шесть уравнений, аналогичных закону Гука для пластины, связывающих между собой соответствующие усилия с составляющими деформациями.
40

Таким образом, для нахождения восьми усилий Мх, My, Qx, Qy, Hx = Ну, Nx, Ny, Тxу = Туx, шести составляющих перемещений u0, v0, w0, κx, κy и 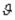 и трех относительных деформаций
и трех относительных деформаций
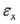 ,
, 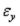 и
и  , т. е. семнадцати неизвестных, имеем 5 + + 3 + 3 + 6 = 17 уравнений.
, т. е. семнадцати неизвестных, имеем 5 + + 3 + 3 + 6 = 17 уравнений.
Число граничных условий для каждой кромки вырезанного элемента равно четырем. Они могут быть геометрическими (равенство нулю перемещений и, v и w), статическими (равенство нулю погонных усилий М, Q, N и Т) или смешанными. Например, для свободно
опертой кромки (  = const, рис. 41) можно написать смешанные условия: и = 0, w = 0, Мx = 0, Nx = 0. Общее число условий равно числу произвольных постоянных, получающихся при интегрировании дифференциальных уравнений.
= const, рис. 41) можно написать смешанные условия: и = 0, w = 0, Мx = 0, Nx = 0. Общее число условий равно числу произвольных постоянных, получающихся при интегрировании дифференциальных уравнений.
Рис. 41
Решение системы семнадцати уравнений при заданных граничных условиях в общем виде в ряде случаев не может быть получено. Поэтому пользуются обычно решениями для частных случаев формы оболочки и ее нагружения, дающих возможность упростить общие уравнения.
Одно из простых решений получается в тех случаях, когда напряжениями изгиба можно пренебречь, учитывая лишь напряжения, связанные с деформацией срединной поверхности. Соответствующая теория называется безмоментной или мембранной. Она применима в тех случаях, когда радиусы срединной поверхности изменяются плавно, оболочка не имеет переломов и резких изменений толщины. Нагрузка, действующая на оболочку, тоже должна изменяться плавно или быть постоянной.
По безмоментной теории предполагается, что изгибающие и крутящие моменты, а также поперечные силы отсутствуют, т. е.
Mx = My = H = Qx = Qy = 0,
и остаются лишь продольные силы Nx и Ny и сдвигающие силы Тxy = Тyx.
В случае, если оболочка представляет собой оболочку вращения и нагрузка симметрична относительно оси вращения и нормальна к срединной поверхности оболочки, сдвигающие силы Тxу = Тух также отсутствуют и остаются только продольные силы; меридиональные Nm и окружные NT.
При постоянной интенсивности давления q и постоянных радиусах R1 и R2 главных кривизн меридиональные, так же как и окружные погонные силы Nm и NT, одинаковы во всех точках и напряженное состояние оболочки однородное.
41
2.3 Оболочка вращения, нагруженная нормальным давлением
На рис. 42 показана оболочка вращения с постоянной толщиной, нагруженная нормальным давлением интенсивностью q. Вырежем из нее двумя меридиональными сечениями 1 и 2 и двумя экваториальными сечениями 3 и 4 малый элемент abcd, имеющий размеры ds1 и ds2. Радиусы кривизны R1 и R3
Рис. 42
кривых 1 и 3 в какой-либо точке К оболочки совпадают, так как оба радиуса направлены по нормали к касательной плоскости I – I в этой точке. Центр кривизны 01 меридиональной кривой может лежать как внутри очертания оболочки, так и вне оболочки в зависимости от того, выпуклая она или вогнутая, и в зависимости от величины радиуса кривизны R1, а центр кривизны 02 лежит на оси вращения  . Геометрическое место радиусов R3 представляет собой коническую поверхность с вершиной, расположенной на оси
. Геометрическое место радиусов R3 представляет собой коническую поверхность с вершиной, расположенной на оси  .
.
Составим условия равновесия элемента abcd в виде суммы проекций всех сил, действующих на элемент, на нормаль п к оболочке, проведенную в центре элемента (рис. 43,а). Так как по четырем граням, которыми выделен элемент, в силу симметрии оболочки и нагрузки относительно оси вращения касательные напряжения отсутствуют, эти грани представляют собой главные площадки, а нормальные напряжения − главные напряжения:
меридиональное 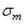 и окружное
и окружное  .
.
На рис. 43,б показаны три проекции элемента abсd и напряжения, действующие по его граням. Сумма проекций усилий, приложенных к элементу, на нормаль
,
получаем
42
или, после сокращения на произведение ds1ds2 и переноса давления q и толщины h в правую часть,
. |
(2.2) |
Так как погонные усилия, действующие в экваториальном и меридианном сечениях,
 ,
,
можно получить уравнение (2.2), записанное через погонные усилия,
. |
(2.3) |
Уравнение (2.2) или его разновидность (2.3) называется уравнением Лапласа.
а б
Рис. 43
При выводе формул Лапласа внутреннее давление q считалось положительным. Наружное давление q следует подставлять в формулы (2.2) и (2.3) со знаком минус. Радиусы кривизны R1 и R2 считаются положительными для выпуклого сосуда и отрицательными для вогнутого. При пользовании указанными правилами знаков положительное усилие или напряжение соответствует растяжению, а отрицательное − сжатию.
Уравнение Лапласа содержит два неизвестных − меридиональные и окружные напряжения (или усилия). Для их определения необходимо дополнительное уравнение, которое получается при отсечении от оболочки части ее и составлении условия равновесия для оставшейся части. Рассекающая плоскость Р − Р обычно выбирается нормальной к оси вращения 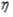 , но стенка оболочки пересекается по нормали к меридиану (рис. 44). Отбрасывать удобно ту часть, на которой находятся опорные связи, − верхнюю на рис. 44,а и нижнюю на рис. 44,б и в.
, но стенка оболочки пересекается по нормали к меридиану (рис. 44). Отбрасывать удобно ту часть, на которой находятся опорные связи, − верхнюю на рис. 44,а и нижнюю на рис. 44,б и в.
43
б
а
в
Рис. 44
Уравнение равновесия оставшейся части подвешенного сосуда, показанной на рис. 44,а сплошной линией, составляем в виде суммы проекции на ось вращения  всех сил, действующих на эту часть:
всех сил, действующих на эту часть:
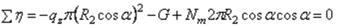 ,
,
откуда
. |
(2.4) |
В случае опертой оболочки, |
показанной на рис. 44,б и в, второй член G числителя |
формулы (2.4) будет отрицательным. В формуле (2.4) приняты обозначения: qz − гидростатическое или газовое давление на уровне Р − Р (в случае гидростатического давления qz = γ (Н − z), где  − объемный вес жидкости); G − вес жидкости в оставшейся части сосуда;
− объемный вес жидкости); G − вес жидкости в оставшейся части сосуда;  − угол между касательной к меридиональному сечению на уровне Р − Р и осью вращения.
− угол между касательной к меридиональному сечению на уровне Р − Р и осью вращения.
Первый член в числителе формулы (2.4) выражает вес цилиндра, имеющего радиус основания R2 cos и высоту (H – z ). Поэтому в случае опертой оболочки числитель
и высоту (H – z ). Поэтому в случае опертой оболочки числитель
44

формулы (2.4) представляет собой разность весов цилиндра с основанием, равным площади сечения Р − Р, и части сосуда, расположенной выше этого сечения. Эта разность пропорциональна разности объемов, показанных на рис. 44,б и в штриховкой. Если разность положительна, усилие Nm растягивающее (объем цилиндра больше объема сосуда − рис. 44,б), если разность отрицательна, усилие Nm сжимающее (объем цилиндра меньше объема сосуда − рис. 44,в).
Рассмотрим применение этих уравнении в частных случаях.
1. Шаровая оболочка с радиусом R, нагруженная радиальной равномерно распределенной нагрузкой (рис. 45).
Рис. 45
В этом случае в силу шаровой симметрии
(2.5)
и напряжение σ в любой точке и по любому нормальному сечению может быть найдено без помощи дополнительного уравнения. Подстановка значений (2.5) в уравнение (2.2) дает
.
Относительная окружная и равная ей относительная меридиональная деформации по закону Гука
. |
(2.6) |
С другой стороны, относительная окружная деформация
. (2.7)
Приравняв друг другу выражения (2.6) и (2.7), найдем радиальное перемещение
или, заменив σ его выражением (2.6), получим:
.
45
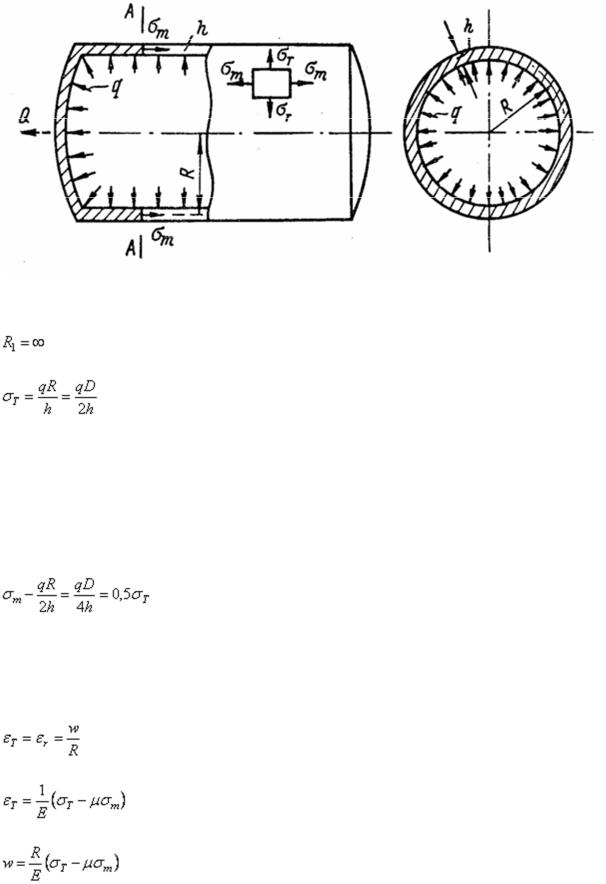
2. Цилиндрическая оболочка с радиусом R, нагруженная нормальной к поверхности равномерно распределенной нагрузкой q (рис. 46).
Рис. 46
В этом случае главные радиусы кривизны
и R2 = R.
Поэтому на основании формулы (2.2) окружное (экваториальное) напряжение
,
где D − диаметр цилиндра.
Второе главное напряжение − меридиональное напряжение 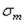 − находится из условия равновесия части оболочки слева от сечения А − А. Равнодействующая Q давления на торец уравновешивается усилиями, направленными вдоль образующей, действующими по кольцу, получающемуся при рассечении цилиндра плоскостью А − А. Тогда
− находится из условия равновесия части оболочки слева от сечения А − А. Равнодействующая Q давления на торец уравновешивается усилиями, направленными вдоль образующей, действующими по кольцу, получающемуся при рассечении цилиндра плоскостью А − А. Тогда
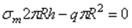 ,
,
откуда
.
При отсутствии торцовых днищ в коротком цилиндре  = 0, а в длинном
= 0, а в длинном 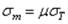 .
.
Относительная окружная деформация 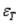 для цилиндрической оболочки вычисляется так же, как и для шаровой. Такую же величину имеет и относительная радиальная
для цилиндрической оболочки вычисляется так же, как и для шаровой. Такую же величину имеет и относительная радиальная
деформация  :
:
, |
(2.8) |
но по закону Гука |
|
. |
(2.9) |
Приравняв выражения (2.8) и (2.9), найдем радиальное перемещение
46
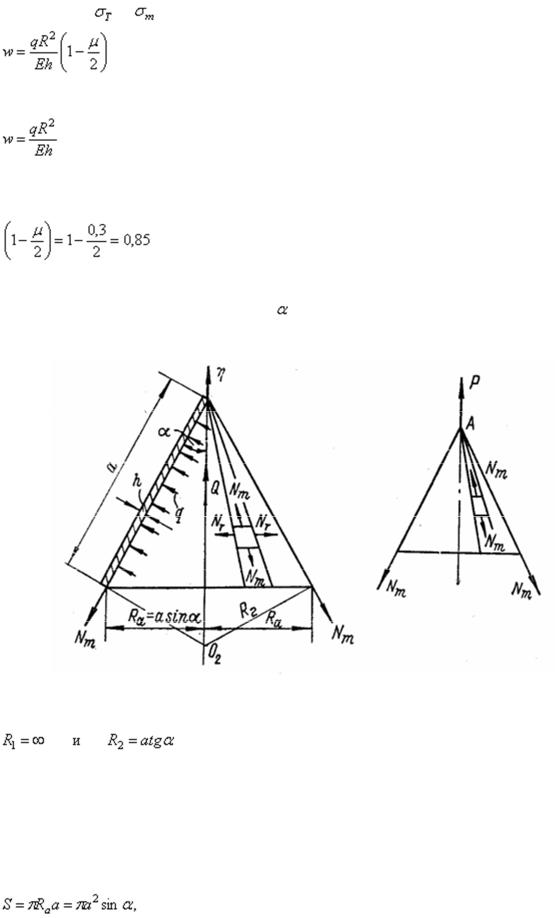
или, заменив |
и |
их выражениями, |
|
. |
(2.10) |
При отсутствии торцовых днищ в короткой оболочке напряженное состояние можно считать линейным и перемещения вычислять по формуле
. |
(2.11) |
Сравнение формул (2.10) и (2.11) показывает, что при плоском напряженном состоянии радиальное перемещение оболочки меньше, чем при линейном; для стальной оболочки
коэффициент уменьшения |
|
|
|
|
|
, |
|
|
|
т. е. перемещения при плоском состоянии составляют 85% |
от перемещений, |
|||
вычисленных в предположении линейного состояния. |
|
|
||
3. |
Коническая оболочка с углом |
при вершине, |
нагруженная нормальной к |
|
поверхности равномерно распределенной нагрузкой q (рис. 47,а). |
|
|||
|
а |
|
б |
|
Рис. 47
В этом случае главные радиусы кривизны
и из уравнения (5.3) находим
 .
.
Из уравнения равновесия 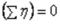
 ,
,
где Q − равнодействующая проекции на ось  нормальных давлений на оболочку. Так как при длине образующей а боковая поверхность оболочки
нормальных давлений на оболочку. Так как при длине образующей а боковая поверхность оболочки
47
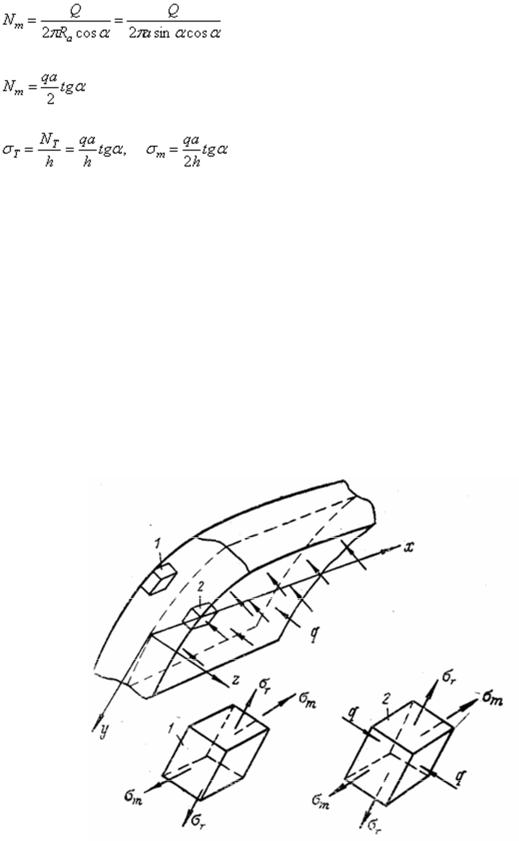
равнодействующая
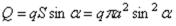 .
.
Меридиональное усилие
. |
(2.12) |
Если в это выражение подставить найденное значение Q, то
.
и
.
4. Выражение для меридионального усилия Nm справедливо также в случае сосредоточенной силы Р, приложенной к вершине А конической оболочки по ее оси (рис. 47,б). В формуле (2.12) равнодействующую Q нужно в этом случае заменить на Р. Так как при этом распределенное давление q равно нулю, из уравнения Лапласа (2.3) следует, что
окружное усилие NT и окружное напряжение 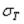 равны нулю.
равны нулю.
Две главные площадки оболочки вращения совпадают с экваториальным и меридиональным сечениями. Третья главная площадка нормальна к первым двум и параллельна срединной поверхности. При действии на оболочку внутреннего нормального давления элемент 1, выделенный у ее наружной поверхности (рис. 48), находится в плоском напряженном состоянии, а у внутренней поверхности (элемент 2) − в объемном. Третья главная площадка испытывает главное напряжение − q, однако меридиональное и
экваториальное напряжения, имеющие, как видно из уравнения Лапласа, порядок 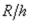 ,
,
значительно больше (в 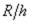 раз), чем q. Поэтому обычно третьим главным напряжением q пренебрегают и считают, что материал оболочки по всей толщине стенки находится в плоском напряженном состоянии.
раз), чем q. Поэтому обычно третьим главным напряжением q пренебрегают и считают, что материал оболочки по всей толщине стенки находится в плоском напряженном состоянии.
Рис. 48
48

2.4 Изгиб цилиндрической круговой оболочки
Основные зависимости для случая изгиба замкнутой круговой цилиндрической оболочки, нагруженной равномерным радиальным давлением q (рис. 49), можно получить без использования общей теории оболочек. Считаем, что отношением толщины оболочки
к радиусу кривизны 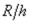 можно пренебречь ввиду его малости по сравнению с единицей. В таком случае при изгибе деформации и напряжения пропорциональны расстоянию z от волокна до срединной поверхности, а при отсутствии изгиба распределяются равномерно по толщине оболочки.
можно пренебречь ввиду его малости по сравнению с единицей. В таком случае при изгибе деформации и напряжения пропорциональны расстоянию z от волокна до срединной поверхности, а при отсутствии изгиба распределяются равномерно по толщине оболочки.
Рис. 49
Выделим из оболочки элемент двумя поперечными сечениями, находящимися на расстоянии dx друг от друга, и двумя радиальными сечениями, образующими между
собой угол 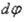 . Усилия, действующие на вырезанный элемент, показаны на рис. 50.
. Усилия, действующие на вырезанный элемент, показаны на рис. 50.
Рис. 50
Вследствие круговой симметрии оболочки и нагрузки относительно оси цилиндра поперечная силы Qy и крутящие моменты Н отсутствуют, а продольная сила Ny и изгибающий момент My постоянны по длине окружности. Вследствие того, что давление q
49
