10621

- 100 -

- 101 -

Теперь для построения М достаточно вычислить ее значение в точке

z = 4: M(4) = Mq(4) + Mp(4) + MM(4) = - 1 + 4 + 1 = 4кНм (рис.3.6б).

Переходим к построению эпюры Q.

На первом участке она обратносимметрична эпюре, приведенной на рис.3.4. На незагруженных участках балки эпюру Q легко построить по эпюре М, воспользовавшись зависимостью Q = dM / dz = tgα:

– на втором участке (2 ≤ z < 4) :

Q = tgα1= (4+2)/2=3 кН;

– на третьем (4 ≤ z < 6) :

Q = – tgα2= – (4– 2)/2= – 1 кН;

– на последнем четвертом участке (6 ≤ z < 8) М = const, поэтому Q = 0

(рис.3.6в).

По эпюре Q находим реакции опор (рис.3.6г) и выполняем статическую проверку правильности решения:

- 102 -

ГЛАВА 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЙ

Прочность балки при изгибе, в отличие от ЦРС, зависит не только от площади поперечного сечения, но и от формы этого сечения. В этом нетрудно убедиться на примере деревянной линейки, положенной плашмя или поставленной на ребро.

4.1. Статические моменты сечения

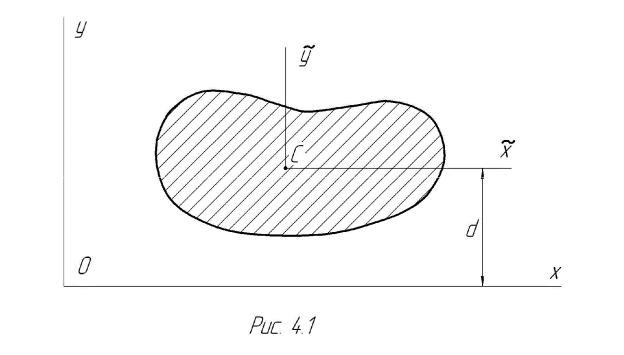
Рассмотрим произвольное поперечное сечение площадью F в системе координат Оху (рис.4.1).

Центр тяжести этого сечения, как известно из ТМ, определяется координатами:

где Sx , S y - статические моменты сечения относительно осей Ox и Oy.

Очевидно, что каждый из этих моментов можно рассматривать как предел суммы элементарных площадей Fi , на которые разбито сечение, умноженных

на взятые со знаком ± расстояния от них до этих осей:

тельно центральных осей равны нулю.

Отметим, что статические моменты измеряются в м3 или см3 и называются моментами первого порядка, т.к. равны произведению площади на расстоя-

ния в первой степени.

4.2. Моменты инерции сечения

Эти моменты являются моментами второго порядка и определяются следующим образом.

Момент инерции сечения относительно центра (оси) равен сумме произведений элементарных площадей на квадраты расстояний до этого центра (оси).

Переходя в этих суммах к пределу при стремлении элементарных площадей Fi к нулю, получим:

С учетом зависимости r = x2 + y2 получим из этих формул соотношение:

= + (4.5)

Jo J x J y

т.е. момент инерции относительно центра или полярный момент инерции равен сумме осевых.

ПРИМЕЧАНИЯ:

1.В этом курсе мы ограничимся изучением прямого изгиба и симметричных сечений, поэтому не будем рассматривать другие моменты инерции, необходимые для характеристики несимметричных сечений.

2.Моменты инерции измеряются в м4 или в см4 и, в отличие от статических моментов, всегда положительны.

-104 -

3.Радиусы инерции сечения относительно центра (io), или оси (iz) равны:

io = J o 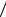F , iz = J z F .

4.3. Моменты инерции относительно параллельных осей

Для определения геометрических характеристик сложных сечений, составленных из стандартных прокатных профилей (двутавр, швеллер и др.), нужно знать соотношения между моментами инерции этих элементов относительно собственных центральных осей, приведенными в сортаменте, и моментами инерции относительно центральных осей всего сечения.

Таким образом, момент инерции сечения относительно какой-либо оси равен моменту инерции относительно параллельной ей центральной оси плюс площадь сечения, умноженная на квадрат расстояния между осями:

4.4. Моменты инерции простых сечений

К числу наиболее распространенных форм поперечных сечений балок, особенно деревянных, относятся прямоугольник и круг.

Прямоугольник. Рассмотрим поперечное сечение балки шириной b и вы-

- 105 -

Круг. Определим вначале момент инерции круга радиуса R относительно его центра О (рис.4.3). Проще всего вычислить соответствующий интеграл в (4.4), разбивая круг на кольца шириной dr и полагая dF равной площади этого кольца.

С точностью до бесконечно малых первого порядка dF = 2πr ×dr , поэто-

му:

Пример 4.1. Вычислить центральный момент инерции балки треугольного поперечного сечения (рис.4.4а).

Решение. Рассмотрим сечение в виде квадрата со стороной b = a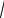2 (рис.4.4б). Полагая в (4.7) h = b , найдем момент инерции квадратного сечения

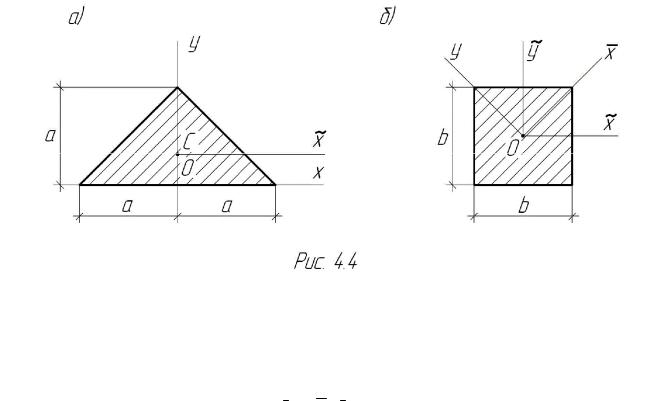
Воспользовавшись для квадрата соотношением (4.5), получим:

- 106 -

Из (4.4) следует, что момент инерции составного сечения относительно какой-либо оси равен сумме моментов инерции отдельных частей этого сече-

_

ния относительно той же оси. Поэтому, представив квадрат на рис.4.4б в виде

двух треугольников, разделенных осью Оx , получим, что момент инерции каждого из них относительно оси Оx будет равен:

J xТР = 1 J xКВ = b4 / 24 .

2

Возвращаясь к рис.4.4а, найдем для заданной балки:

J xТР = b4 / 24 = 4a4 / 24 = a4 / 6 .

- 107 -

ГЛАВА 5. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ

5.1. Предпосылки расчета

Мы выяснили, что напряжения в поперечном сечении балки статически эквиваленты внутренним усилиям, которые находят из условий равновесия ее отсеченной части. Однако, для расчета на прочность недостаточно определить М и Q − нужно знать именно напряжения σ и τ . Чтобы выразить последние через внутренние усилия (1.2), надо ввести дополнительные гипотезы, отражающие особенности деформирования балки и распределение напряжений по площади ее сечения, − подобные введенной при рассмотрении ЦРС.

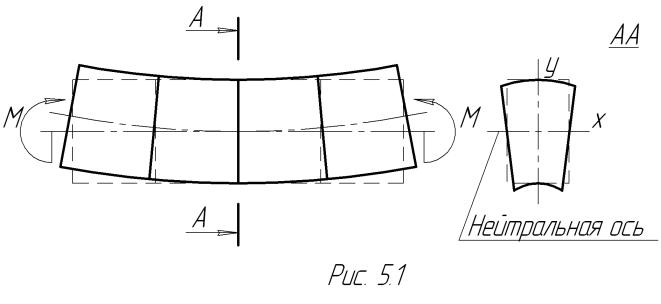
Для обоснования соответствующих предпосылок рассмотрим балку прямоугольного поперечного сечения в условиях чистого изгиба с нанесенной на ее боковой поверхности ортогональной сеткой (рис.5.1).

Как видим, ее нижние волокна − растягиваются, верхние − сжимаются, а образующие нейтральный слой − остаются недеформированными. При этом размеры сечения по оси Оу не меняются, а сами сечения остаются перпендику-

лярными к изогнутой оси балки.

Это позволяет ввести в рассмотрение две гипотезы.

1.Статическая гипотеза. Горизонтальные слои балки не давят друг на друга, т.е. σ у = 0 .

2.Кинематическая гипотеза. Сечения, перпендикулярные к оси балки до деформации, остаются перпендикулярными к ее изогнутой оси. При этом перемещения точек нейтрального слоя балки вдоль осей Ох и Оz равны нулю.

Как показывает опыт, применение этих гипотез оправдано и в случае поперечного изгиба балки.

- 108 -

Определение. Прямая, полученная пересечением нейтрального слоя с плоскостью поперечного сечения, называется его нейтральной осью.

ПРИМЕЧАНИЯ:

1. Кинематическая гипотеза, известная как гипотеза плоских сечений Я.Бернулли, фактически применялась нами еще в параграфе 2.1 при рассмотрении деформации ЦРС: вве-

денная там предпосылка о постоянстве σz в поперечном сечении стержня с учетом закона Гука (2.6) означала постоянство ε z , а в силу (2.4) − также и w.

2. Рассмотренные гипотезы, особенно в случае поперечного изгиба, соответствуют действительности только приближенно:

-вблизи мест приложения нагрузки нарушается статическая гипотеза о несдавливании горизонтальных слоев;

-первоначально плоские поперечные сечения при деформации могут искривляться и так далее.

Тем не менее, полученные на их основе результаты расчета вполне отвечают потребностям инженерной практики.

5.2.Перемещения и деформации

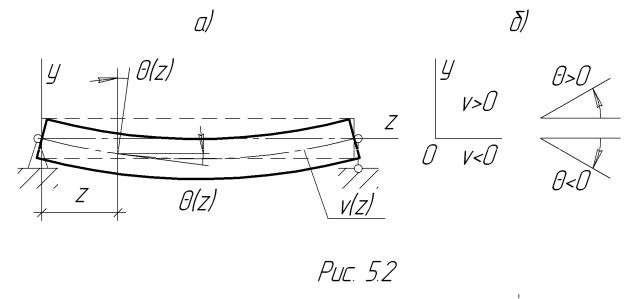
Рассмотрим балку в системе координат Oxyz , где ось балки совпадает с осью Оz , проходящей через нейтральные оси сечений (рис.5.2а).

z

Прогибами балки называются перемещения точек ее оси, которые с учетом кинематической гипотезы возможны только в направлении оси Оу .

Изогнутой осью балки называется кривая v(z) , которую принимает ось

балки при деформации.

Угол поворота сечения θ(z) равен углу наклона касательной к изогнутой оси балки. На основании гипотезы малости перемещений (параграф 1.4):

- 109 -

Правило знаков − в соответствии с рис.5.2б.

Отметим, что в силу гипотезы Бернулли перемещения всех точек балки описываются перемещениями точек, лежащих в плоскости ее симметрии Oyz.

Чтобы проследить за точками балки, не лежащими на ее оси, рассмотрим консоль длиной z, защемленную на левом конце и загруженную на правом − моментом (рис.5.3).

Зафиксируем на свободном конце балки точку А − пусть она находится на расстоянии у от нейтральной оси, проходящей через точку С, и в результате деформации занимает в пространстве положение А′ .

Из А′ВС′ найдем модуль проекции вектора перемещения АА′ на ось Оz:

|w(z)| = A′B = A′C′sin θ = y sin θ. Принимая во внимание (5.1) и заменяя приближенное равенство строгим, получим с учетом знака w(z):

Таким образом введенные в предыдущем параграфе гипотезы, позволяют выразить перемещения и деформации точек балки через уравнение ее изогнутой оси v(z) .

ПРИМЕЧАНИЯ:

1. Фактически изменение длины волокна балки, проходящего через точку А ее сечения, равно не отрезку A′B = y sin θ , а отрезку A′B′ = y tgθ, и (5.1) означает, что A′B′

A′B (рис.5.3б).