
10520
.pdf
70
в грунтах после землетрясения. Применяемые при расчетах конструкций зданий акселерограммы неполно отражают характер сейсмического воздействия, в этих акселерограммах не содержатся длиннопериодные составляющие.
2. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1
Определение частот собственных колебаний систем с одной степенью свободы
Числом степеней свободы механической системы называют число параметров, полностью определяющих положение всех точек системы. В
динамике число степеней свободы напрямую зависит от количества сосредоточенных масс системы и от количества независимых перемещений этих масс.
В практике применяются следующие основные методы составления уравнений движения:
Принцип Даламбера Уравнение динамического равновесия можно получить из уравнения
статического равновесия добавлением инерционных сил. Как известно,
сила инерции J по величине равна произведению массы на ускорение:
= ̈=
2
2
и направлена в противоположную ускорению сторону. Здесь m – масса, y
– перемещение, ̈= 2 – ускорение, t – время.
2
Энергетический метод При решении задач о собственных колебаниях упругих консервативных
систем часто используется закон сохранения механической энергии,
согласно которому сумма потенциальной и кинематической энергий колебательной системы постоянна во времени:
+ =
71
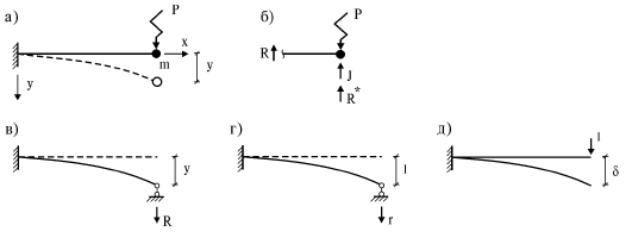
Рассмотрим собственные колебания системы с одной степенью свободы на основе принципа Даламбера (кинетостатического метода):
- рассмотрим движение массы относительно ее исходного положения равновесия.
Рис. 1.1 – Колебательная система с одной степенью свободы.
− − − = 0 (, , )
где = ̈– сила инерции, – сила упругости балки, - сила сопротивления среды движению массы.
Силу упругости можно определить из решения задачи статики в двух формах − в форме метода перемещений и в форме метода сил. Вначале применим метод перемещений. С этой целью в свободном правом конце балки введем вертикальную связь, и дадим ей такое же перемещение y, какое возникает при колебаниях (рис. 1.1 в). Реакция этой связи будет равна силе отпора балки R. Если балка упругая, эта сила пропорциональна отклонению балки:
=
где – упругая характеристика балки, называемая жесткостью. Она равна реакции в связи при ее смещении на единицу (рис.1.1 г).
Подставив в (,,) выражения сил инерции и упругости, получим уравнение вынужденных колебаний системы с одной степенью свободы в форме метода перемещений:
̈+ + = (… )
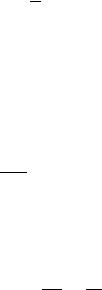
72
Иногда его называют уравнением колебаний в прямой форме. Для использования метода сил рассмотрим другое состояние балки, когда в направлении колебаний массы приложена единичная сила (рис. 1.1д).
Перемещение этой точки под действием единичной силы называется податливостью. Обозначим его буквой δ. На основании теоремы о взаимности работ, возможная работа сил состояния «г» (рис.1.1 г) на перемещениях состояния «д» (рис. 1.1 д) равна возможной работе сил состояния «д» на перемещениях состояния «г», т.е.:
∙ = 1 ∙ 1
Отсюда получаем уравнение связи между жесткостью и податливостью
1= (++)
Подставим его в уравнение (…). После деления на m получим:
̈ |
1 |
|
|
|
|
|
+ = |
||||
+ |
|||||
Если обозначить
1 = 2(_)
получаем уравнение вынужденных колебаний системы с одной степенью свободы в форме метода сил (уравнение колебаний в обратной форме):
+̈ 2 + = ( )
Полученные уравнения движения системы с одной степенью свободы в формах метода перемещений (…) и метода сил (**) позволяют вести расчет простейших сооружений на колебания. Выбор конкретного метода зависит от особенностей системы и определяется самим расчетчиком.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 2
Определение частот собственных колебаний систем с несколькими степенями свободы
73
При проектировании сейсмостойких зданий и сооружений особое внимание следует уделять грамотной оценке их динамических характеристик, поскольку сейсмическое воздействие носит ярко выраженный динамический характер.
Из курса строительной механики известно, что при динамических воздействиях на напряженно-деформированное состояние конструктивных элементов влияет не только характер самих воздействий, но и характер распределения входящих в систему масс.
Масса – это количественная мера инертности, то есть физическая величина, показывающая, насколько сложно изменить скорость изучаемого тела. Если рассматривать систему отсчета, связанную с самой массой, то, согласно принципу Д’Аламбера, массу можно считать уравновешенной, если ввести дополнительную силу, называемую силой инерции. Именно с этой силой масса будет «сопротивляться» попытке изменения своей скорости:
| ин| = ∙ = ∙ ̈
Направление силы инерции всегда противоположно
сообщаемому массе.
Поскольку любое сейсмическое воздействие носит динамический характер, во всех точках системы возникают силы инерции, которые оказывают значительное влияние на напряженно-деформированное состояние системы.
Перед началом расчета важно правильно выделить основные особенности работы элементов здания, которые должны быть учтены при выборе расчетной схемы. В общем случае любое здание представляет собой систему с бесконечным числом динамических степеней свободы, поскольку все элементы здания имеют массу и являются упругими. Тем не менее, зачастую возможно пренебречь массами тех или иных элементов, получив при этом конечное число степеней свободы системы.
Например, для каркасных многоэтажных зданий с большой степенью точности можно предположить, что все входящие в систему массы сосредоточены в уровнях перекрытий. Это означает, что здание можно рассмотреть как консольный стержень с количеством сосредоточенных на нем масс, равным количеству этажей здания и жесткостью, эквивалентной жесткости всего здания.
74
Рисунок 2.1.1 Динамическая расчетная схема каркасного здания
При этом, в случае перемены сечений колонн по высоте здания, необходимо учитывать это при определении значения эквивалентной жесткости.
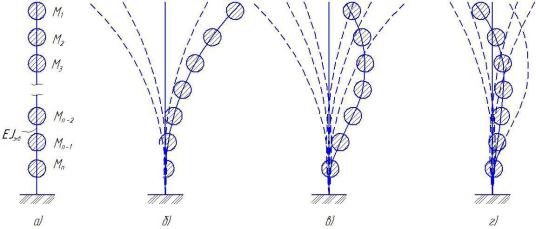
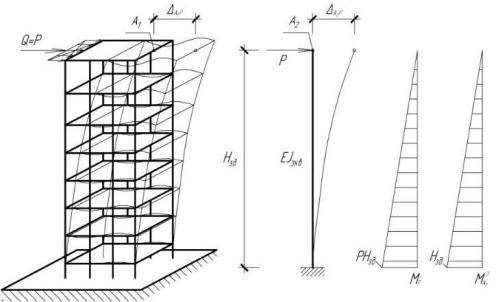
Важной задачей является определение эквивалентной жесткости стержня. Для этого предлагается использовать условие равенства удельного перемещений точек A1 и A2 (рис.2.1.2, а, б) при действии эквивалентных нагрузок. При этом, в случае перемены сечений колонн по высоте здания, необходимо учитывать это при определении значения эквивалентной жесткости.
(а) |
(б) |
(в) |
Рисунок 2.1.2 К определению эквивалентной жесткости стержня
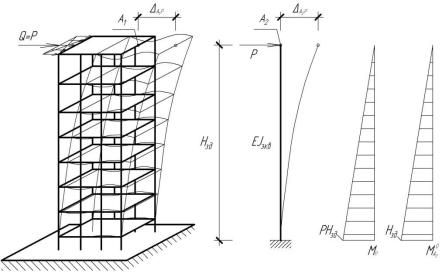
Величину перемещения конечно-элементной модели здания. Мора-Максвелла (рис. 2.1.2, в):
следует определять из статического расчета Перемещение A2 P определяется по формуле
H зд М |
|
A2 |
|
||
M |
|
||||
A2P |
P |
|
|
. |
|
EI |
экв |
||||
0 |
|
|
|
||
Раскроем интеграл (2.2) с помощью правила Верещагина:
A P |
1 |
|
1 |
P H зд H зд |
2 |
H зд |
P H зд3 |
. |
EJ экв |
2 |
3 |
|
|||||
2 |
|
|
|
3EJ экв |
||||
|
|
|
|
|
|
|
|
|
Условие эквивалентности жесткостей примет вид:
A2 P A1P ,
или, с учетом (2.3):
(2.2)
(2.3)
(2.4)
75
A P |
P H зд3 |
|
, |
(2.5) |
|||
3EJ экв |
|||||||
1 |
|
|
|
||||
|
|
|
|
||||
откуда |
|
|
|
|
|
||
EJ |
P H зд3 |
. |
|
(2.6) |
|||
экв |
3 |
A P |
|
1
При этом можно задаваться любой величиной силы P, учитывая, что величина перемещения A1P всегда пропорциональна ей. Для повышения точности расчета
рекомендуется выбирать силу P таким образом, чтобы перемещение A1P не было
исчезающее мало.
Динамической степенью свободы называют наименьшее количество геометрических параметров, определяющих положение системы. Это количество равняется числу независимых возможных колебаний входящих в систему масс. Для расчета системы необходимо не только определить количество возможных колебаний, но и направление каждого из них, поскольку именно в этом направлении и будут прикладываться соответствующие силы инерции.
Собственные колебания – это колебания, совершаемые под действием только внутренних сил. Частота собственных колебаний является важной характеристикой системы, поскольку позволяет спрогнозировать различные резонансные явления, следовательно, она учитывается при определении любых нагрузок, имеющих динамический характер.
Поскольку, в общем случае, здания и сооружения являются механическими системами с N степенями свободы, они имеют N частот и форм собственных колебаний.
Собственные колебания механической системы описываются системой уравнений вида:
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
11М 1 |
|
|
|
a1 |
12 М |
2 a2 |
13 М 3 a3 |
... 1n |
М n an 0 |
|
||||||||
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
21M 1a1 |
22 М 2 |
|
|
a2 |
23 M 3 a3 |
... 2n M n an |
0 |
|
||||||||||
2 |
|
(2.7) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
........................................................................................ |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
n1 M 1a1 |
n2 M 2 a2 |
n3 M |
3 a3 ... |
nn М n |
|
|
|
|
an |
0 |
|
|||||||
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где ai |
– амплитуда колебаний массы Mi , ij |
- |
удельное перемещение точки |
||||||||||||||||
сосредоточения массы Mi от единичного силового фактора, приложенного в точке сосредоточения массы Mj, ω – круговая частота собственных колебаний.
Система уравнений (2.7) имеет 2 вида решений: нулевое, выражающее отсутствие колебаний, и ненулевое, описывающее собственные колебания. Ненулевое решение возможно только в том случае, если определитель матрицы, составленный из коэффициентов системы (2.7) будет равен нулю:

|
|
|
|
|
|
|
|
|
|
|
|
76 |
|
|
|
11М1 |
|
1 |
|
|
|
12 М 2 |
|
13М 3 |
|||
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21M1 |
|
|
|
|
М |
2 |
1 |
|
23M 3 |
||
|
|
|
|
22 |
|
|
|||||||
|
|
2 |
|||||||||||
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
................................................................ |
||||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1M1 |
|
|
|
|
|
n2 M 2 |
|
n3 M 3 ... |
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда уравнение частот примет вид:
... |
1n М n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
... |
2n M n |
|
|
||
|
(2.8) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М n |
1 |
|
|
|
nn |
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
11М1 |
|
1 |
|
|
|
12 М 2 |
|
13М 3 |
||
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21M1 |
|
|
|
М |
2 |
1 |
|
23M 3 |
||
|
|
|
|
22 |
|
|
|||||||
det W |
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
................................................................ |
|||||||||
|
|
|
n1M1 |
|
|
|
|
n2 M 2 |
|
n3 M 3 ... |
|||
... |
1n М n |
|
|
|
|
... |
2n M n |
|
0 |
||
|
|
|
|
|
|
|
М n |
1 |
|
|
|
nn |
|
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
Решениями уравнения (7) являются корни многочлена n-ной степени:
a |
n a n 1 |
a |
n 2 .... a |
n 1 |
a |
n |
0 |
, |
0 |
1 |
2 |
|
|
|
|
где 12 .
(2.9)
(2.10)
Для зданий с большим количеством этажей вычисления становятся очень громоздкими, поскольку возникает необходимость раскрытия определителя матрицы n-ного порядка, после чего необходимо определить корни многочлена n- ной степени.
Для определения собственных частот предлагается использовать простой перебор случайных значений . Тогда выражение (9) будет представлять собой определитель числовой матрицы, вычисление которого возможно с помощью ПК.
Помимо этого, существуют приближенные методы определения частот собственных колебаний, например, метод Релея, метод приведенной массы и пр.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3
ОПРЕДЕЛЕНИЕ СОБСТВЕННОЙ ЧАСТОТЫ ПОСТУПАТЕЛЬНЫХ КОЛЕБАНИЙ ЗДАНИЙ
Найдем частоты изгибных форм колебания здания [4,10,11,31]:
( − |
1 |
) + |
|
+ + + |
|
|
|
|
= 0 |
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
11 1 |
2 |
1 |
|
|
|
2 12 |
|
2 |
|
|
3 13 |
|
1 |
|
|
|
|
|
|
||||||
+ ( |
|
|
− |
1 |
) |
|
|
+ |
|
+ + |
|
|
|
= 0 |
(2.6) |
||||||||||
|
|
|
2 |
3 |
|
|
|||||||||||||||||||
1 21 1 |
22 |
21 |
|
|
2 |
|
|
|
3 23 |
|
2 |
|
|
|
|||||||||||
… … … … … … … … … … … … … … … … … … … … … … |
|
|
|
|
|
||||||||||||||||||||
+ |
|
|
|
+ |
|
|
|
|
+ + ( − |
1 |
) |
|
|
= 0 |
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||
{ 1 1 1 |
2 2 |
|
2 |
|
3 3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||

77
где – удельное перемещение сосредоточения i-той массы от единичной силы, приложенной в точке сосредоточения j-той массы;
- частота собственных колебаний системы.
На основании уравнения частот, отбросив амплитуды колебаний составим матрицы частот (2.7):
|
( − |
1 |
) |
|
… |
|
|
|
|
|||||
|
|
|
|
|
||||||||||
|
11 1 |
|
2 |
2 12 |
|
|
1 |
|
|
|||||
|
| |
|
|
|
|
1 |
|
|
|
|
|
| |
|
|
det = |
|
( |
− |
) … |
|
= 0 |
(2.7) |
|||||||
|
|
|||||||||||||
1 21 |
22 21 |
|
2 |
|
|
2 |
||||||||
|
| … … … … … … … … … … … … … … … … | |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
… ( |
|
− |
|
|
) |
|
|
||||
|
|
|
|
|
||||||||||
|
1 1 |
|
2 2 |
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Раскрывая определитель матрицы коэффициентов системы уравнений амплитуд (W) (2.7) найдем корни многочлена n-ной степени (2.8):
|
−1 |
−2 |
+ + |
+ = 0, |
(2.8) |
|
+ |
+ |
|||
0 |
1 |
2 |
−1 |
|
|
где = 12.
В связи с возникновением необходимостью раскрытия определителя матрицы n-ного порядка, вычисление зданий с большим количеством этажей становится громоздким.
Для определения первой и последующих собственных частот, используя метод последовательного приближения, выражение (2.7) будет представлять собой определитель числовой матрицы.
При определении частотных характеристик одной из важных задач является определение эквивалентной жесткости стержня. Для решения этой задачи воспользуемся условием равенства удельных перемещений А1 и А2 (рис 2.8. а, б) при действии эквивалентной нагрузки.
78
(а) |
(б) |
(в) |
Рис. 8. К определению эквивалентной жесткости стержня
Значение удельного перемещения верхней точки здания следует определять из статического расчета конечно-элементной модели рассматриваемого здания, построенного в ПВК SCAD. Перемещение 2
определяется по формуле Мора-Максвелла (рис. 8. в) [27,10,11,29,30]:
|
|
|
|
|
|
|
зд |
|
̅ |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 = ∫ |
|
|
|
|
|
|
|
|
2 |
. |
|
|
|
(2.9) |
|||||
|
|
|
|
|
|
|
экв |
|
|
|
|
|||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Раскроем интеграл (2.9) с помощью правила Верещагина: |
|
|||||||||||||||||||||
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
∙ 3 |
|
|||
|
= |
|
∙ |
|
|
∙ ∙ |
|
|
∙ ∙ |
|
|
|
∙ = |
зд |
. |
(2.10) |
||||||
2 |
|
2 |
|
|
3 |
|
|
|||||||||||||||
|
|
|
|
зд |
|
зд |
|
зд |
3 |
|
||||||||||||
|
|
экв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
экв |
|
|
Условие эквивалентности жесткостей примет вид: |
|
|||||||||||||||||||||
|
|
|
|
|
|
2 = |
1, |
|
|
|
|
|
|
(2.11) |
||||||||
или, с учетом (2.10): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
∙ 3 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
= |
|
|
|
зд |
, |
|
|
|
|
|
|
(2.12) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
3 экв |
|
|
|
|
|
|
|
||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ 3 |
|
|
|
|
|
|
|
|||||
|
|
|
|
= |
|
|
|
|
|
зд |
. |
|
|
|
|
|
|
(2.13) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
экв |
|
|
3 ∙ 1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Выполняя расчет по определению эквивалентной жесткости значение Р |
||||||||||||||||||||||
можно задать любой величины, так как величина перемещений |
1 всегда |
|||||||||||||||||||||
79
пропорциональна ей. Силу Р рекомендуется выбирать таким образом, чтобы величина перемещения 1, для повышения точности расчета не была исчезающе мала[11,30].
Составление матрицы податливости
Для решения задачи по определению первой собственной частоты изгибных колебаний рассмотрим двенадцатиэтажный каркасный жилой дом.
Элементы матрицы перемещений-частот W определяются с помощью ПВК
«Полюс» с учетом правила взаимности удельных перемещений: =
(рис.9.).
На основании данных расчета удельных перемещений от единичной нагрузки с использованием ПВК «Полюс», когда здание рассматривается как консольный стержень, составим матрицу удельных перемещений от единичной нагрузки (единичных перемещений) согласно уравнению 2.14.
Результаты расчета представлены в таблице В1.1 приложения В1.
