
10380
.pdf
- 80 -
i 1, i Xi 1 + i,i Xi + i+1, i X i+1+ i p0 = 0. (4.17)
Это уравнение называется «уравнением трех моментов», поскольку в качестве неизвестных выступают изгибающие моменты над i-й опорой неразрезной балки и еще над двумя опорами, смежными с ней.
Рис. 4.12
Примечание
В качестве исходной балки для получения неразрезной помимо простой двухопорной балки можно взять балку с одним или двумя жесткозащемленными концами.
4.8. Примеры расчета СНС
При расчете СНС реакции связей могут оказаться равными нулю так же, как и при определении опорных реакций СОС.
- 81 -
Пример 4.5. Построить эпюру MP в раме от заданной нагрузки, полагая EJ
= const (рис. 4.13, а).
Решение. Заданная система имеет только одну лишнюю связь, поэтому в качестве основной можно взять систему, полученную из заданной устранением опоры А. Связь в точке С является безусловно необходимой, и ее устранение приводит к мгновенно изменяемой ОС.
а) |
C |
б) |
|
C |
|
З.С. |
|
|
M10 |
|
|
A |
X1=1 |
B |
|
B |
|
||
A |
|
|
||
|
|
|
в) |
|
C г) |
C |
|
MP0 |
|
MP |
A |
B |
A |
B |
Рис. 4.13
Строим эпюры M 0 и M 0 (рис. 4.13, б-в) для вычисления коэффициента и
1 p
свободного члена канонического уравнения МС:
11 X1 + 1p0 = 0. |
(а) |
Как видим, эти эпюры взаимно ортогональны, 11 0, 1p0 = 0, и решением (а) будет X1 = 0. Поэтому M = M 0 + M 0X = M 0 (рис. 4.13, г).
p |
p |
1 1 |
p |
Как уже отмечалось, для системы с одной лишней связью простота решения задачи полностью определяется видом эпюры Mp0.
Пример 4.6. Построить эпюру MP в раме от заданной нагрузки, полагая EJ
= const (рис. 4.14, а).
Решение. Отбросив в ЗС опору А, придем к ОС, которой соответствуют |
||||
эпюры M 0 |
и M 0 (рис. 4.14, б-в). |
|
|
|
1 |
p |
0 |
= M 0 (рис. 4.14, г) и M |
0, при этом |
Другой ОС соответствуют эпюры M |
||||
|
|
1 |
1 |
P |
последняя заметно проще эпюры Mp0 (рис. 4.14, д).

|
|
|
|
|
- 82 - |
а) |
q |
B |
|
C |
б) |
|
|
|
|
||
|
|
|
З.С. |
|
l |
|
A |
|
|
|
|
|
|
l |
l |
|
|
|
|
|
|
|
|
в) |
|
|
|
|
г) |
|
ql2/2 |
|
|
|
|
|
|
|
MP0 |
|
|
C
 B l
B l
M10
A X1=1
|
C |
l |
X1=1 |
|
|
|
M10 |
A |
|
д)
ql2/8
е) |
C |
ql2/40 |
B |
MP0 |
MP |
A |
|
Рис. 4.14
Вычисляя коэффициенты канонического уравнения для EJ = 1, получим:
11 = ( M10 M10) = 5l3/3; ip0 = ( M10 MP0) = – ql4/24,
откуда X1 = – ip0/ 11 = ql/40.
Правильность найденной эпюры Mp = MP0 + M10X1 (рис. 4.14, е) проверяем с помощью кинематической проверки:
1p = (Mp M10) = – (2/3) ( l) (ql2/8) (l/2) + (1/2) ( l) (ql2/40) (2l/3) + |
|
+ l (ql2/40) l + (1/2) l (ql2/40) (2l/3) = (ql2/40)[– (1/24) + 2(1/120) + (1/40)] = 0. |
|
- 83 -
ГЛАВА 5. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ФЕРМ И АРОК МЕТОДОМ СИЛ
5.1. Расчет статически неопределимых ферм
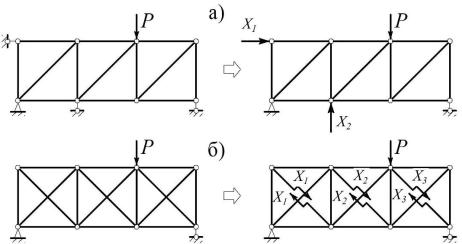
Отметим, прежде всего, что фермы могут быть статически неопределимыми внешним и внутренним образом (рис. 5.1). У первых основная система МС получается отбрасыванием внешних связей и заменой их неизвестными опорными реакциями (рис. 5.1, а), у вторых – опорные реакции можно найти из уравнений статики, а статическая неопределимость проявляется только при определении внутренних усилий. В этом случае ОС получается путем введения разрезов в стержнях фермы, образующих ее пояса или решетку (рис. 5.1, б).
Рис. 5.1
Формально канонические уравнения метода сил для ферм не отличаются от соответствующих уравнений для рам:
n |
|
ij Xj + ip0= 0, (i = 1,2,…, n), |
(5.1) |
j 1
однако теперь в соответствии с примечанием к §3.5 коэффициенты и свободные члены этих уравнений будут определяться только продольными силами:
ij |
= ( Ni0 Nj0 /EF ) ds = ( N 0 |
N 0/EFk)lk , |
(5.2) |
|
ik |
jk |
|
ip0= ( Ni0 Np0/EF ) ds = ( Nik0 Npk0/EFk)lk , |
(5.3) |
||
где lk и EFk – соответственно длина и жесткость k–го стержня фермы, по которым проводится суммирование.
После того как решена система уравнений (5.1), усилия во всех стержнях заданной фермы можно найти по формуле (4.7):
Np = Np0 + Ni0Xi.
-84 -
5.2.Расчет статически неопределимых арок
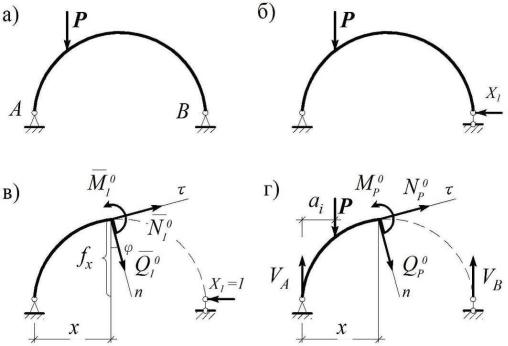
Простейшим примером таких систем является двухшарнирная арка, у которой в отличие от рассмотренной в §2.4 трехшарнирной арки отсутствует ключевой шарнир (рис. 5.2, а).
Рис. 5.2
Основная система для ее расчета может быть получена введением ключевого шарнира, или устранением горизонтальной связи на одной из опор и заменой ее неизвестным распором H = X1 (рис. 5.2, б). Отметим при этом, что вертикальная связь является безусловно необходимой, поскольку ее устранение приводит к мгновенно изменяемой ОС.
Коэффициент 11 и свободный член 1p0 в каноническом уравнении метода
сил:
11 X1 + 1p0 = 0 |
(5.4) |
следует вычислять, учитывая изгибающие моменты и продольные силы и пренебрегая, как обычно, влиянием поперечных сил:
11 |
= ( M10 |
M10 |
/EJ) ds + ( N 10 |
N 10 |
|||
1 |
0 = |
( M 0 |
M 0 |
/EJ) ds + ( N 0 |
N 0 |
||
p |
|
1 |
|
p |
1 |
|
p |
/GF) ds, |
(5.5) |
/GF) ds. |
(5.6) |
Для определения соответствующих усилий надо рассмотреть взятую слева от сечения с абсциссой x часть арки, загруженной вначале силой X1 = 1, а затемзаданной нагрузкой (рис. 5.2, в, г).

-85 -
Впервом случае из условий равновесия арки в целом мы найдем опорные реакции: HA = 1, VA = 0, а затем, рассматривая равновесие ее отсеченной части, так же, как в § 2.4.2 определим усилия:
M10(x) = 1 f (x); Q 10 (x) = 1 sin ; N10(x) = 1 cos . |
(5.7) |
Во втором случае опорные реакции арки, загруженной заданной нагрузкой, равны: HA = 0, VA = VAБ, а ее внутренние усилия:
Mp0(x) = M Б (x); Qp0(x) = Q Б(x) cos ; Np0 = Q Б(x) sin . |
(5.8) |
|||||||||||||||
Подставляя (5.5) (5.8) в (5.4) получим: |
|
|
|
|
|
|
||||||||||
|
|
S |
f (x) M |
0 (x) |
cos N |
|
0 (x) |
|
||||||||
|
|
|
|
|
p |
|
|
|
|
p |
|
ds |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
EJ |
|
|
|
|
EF |
|
|
|
|
|||
X1 = H = 1p0 |
/ 11 = |
|
|
S f |
2 (x) |
cos2 |
|
|
|
|
||||||
|
|
|
|
, |
(5.9) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
ds |
|
||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
0 EJ |
EF |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
после чего внутренние усилия в арке можно найти по формулам (4.7): |
|
|||||||||||||||
|
M = M 0 + M 0X ; |
|
|
|
|
|
|
|||||||||
|
p |
p |
1 |
1 |
|
|
|
|
|
|
|
|
|
|||
|
Q = Q 0 |
+ Q 0X ; |
|
|
|
|
|
|
||||||||
|
p |
p |
1 |
1 |
|
|
|
|
|
|
|
|
|
|||
|
N = N 0 |
+ N 0X . |
|
|
|
|
|
|
||||||||
|
p |
p |
1 |
1 |
|
|
|
|
|
|
|
|
|
|||
Если в последние формулы подставить соотношения (5.7) и (5.8), то нетрудно убедиться, что мы придем к выражениям (2.2) (2.4) для определения внутренних усилий в статически определимой трехшарнирной арке:
Mp = M Б (x) H f (x);
Qp= Q Б (x) cos H sin ;
Np= Q Б (x) sin H cos .
Этим и определяется удобство основной системы, выбранной для расчета.
- 86 -
ГЛАВА 6. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
6.1. Суть метода перемещений. Основная система МП
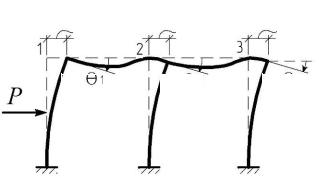
Суть метода перемещений (МП) рассмотрим на примере расчета рамы. Под действием приложенной нагрузки рама деформируется, а ее узлы получают линейные i и угловые i перемещения (рис. 6.1).
Идея МП заключается в том, чтобы выбрать эти перемещения i и i в качестве неизвестных.
Для упрощения расчета будем, как обычно, пренебрегать влиянием продольных сил на деформации. Тогда в нашем примере все линейные перемещения узлов будут равны: i = .
В общем случае для определения числа неизвестных линейных перемещений nл нужно во все жесткие узлы рамы, включая опорные, ввести шарниры, а затем подсчитать число степеней свободы полученной шарнирно-стержневой системы по формуле (1.3):
nл = 2У С СО.
При этом число nл будет равняться числу дополнительных линейных связей, необходимых для превращения полученной системы в геометрически неизменяемую.
Число неизвестных угловых перемещений i равняется, очевидно, числу незакрепленных жестких узлов рамы nу .
Общее число неизвестных метода перемещений n = пу + nл. Таким образом, в рассматриваемом примере n = 3 + 1 = 4.
В дальнейшем все линейные i и угловые i перемещения будем обозначать одинаково Zi.
1 |
2 |
3 |
θ1 |
θ2 |
θ3 |
|
|
|
Рис. 6.1
Основная система МП образуется из заданной системы путем введения дополнительных связей, препятствующих угловым и линейным смещениям ее узлов.

- 87 -
Например, для рамы на рис. 6.2, а основная система получается наложением двух дополнительных связей (рис. 6.2, б). При этом первая связь является моментной и не препятствует линейному смещению соответствующего узла рамы. На схемах такие связи могут обозначать так, как показано на рис. 6.2, в.
Введение связей превращает раму в совокупность однотипных элементов с одним или двумя жестко защемленными концами, для которых известны готовые решения (рис. 6.2, г).
Рис. 6.2
6.2. Канонические уравнения метода перемещений
Если основную систему метода перемещений (ОС МП) загрузить нагрузкой, во введенных связях появятся реакции, которые отсутствовали в заданной системе (поскольку не было самих связей).
Обозначим через R1 и R2 реакции во введенных связях и отметим, что поскольку ОС МП является статически неопределимой, эти реакции могут появляться не только под действием приложенной нагрузки, но и в ответ на кинематические воздействия.
Сообщим введенным связям перемещения Z1 и Z2, равные смещениям заданной системы и потребуем, чтобы ОС вела себя как заданная. Это означает, что реакции во введенных связях от смещения этих связей и от заданной нагрузки в сумме должны равняться нулю:
R1 (Z1, Z2, P) = 0;
R2 (Z1, Z2, P) = 0.

- 88 -
Воспользовавшись принципом суперпозиции, представим эти уравнения в виде:
r11 Z1+ r12 Z2 + R1p0 = 0;
r21 Z1+ r22 Z2 + R2p0 = 0,
где rij реакция во введенной i-й связи от единичного смещения j-й связи, а Rip0реакция в этой связи от заданной нагрузки.
Последние уравнения и называются каноническими уравнениями метода перемещений. В отличие от соответствующих уравнений метода сил эти уравнения имеют не геометрический, а статический смысл.
В общем случае для n неизвестных система канонических уравнений метода перемещений имеет вид:
rij Zj + Rip0 = 0; (i = 1, 2,…, n). |
(6.1) |
Решив эту систему и определив неизвестные Zj, можно найти внутренние усилия по формуле, аналогичной формуле (4.7):
Mp = Mp0 + Mi0Zi. |
(6.2) |
Примечание
Всоответствии с принципом суперпозиции перемещение любой фиксированной точки
iзаданной системы можно найти как сумму двух: перемещения этой точки в ОС МП вследствие смещения введенных связей и ее перемещения в той же системе под действием заданной нагрузки (рис. 6.3):
ip = 0ic + 0ip . |
(6.3) |
Последнее соотношение является аналогом формулы (6.2) для перемещений.
Рис. 6.3
6.3. Вычисление коэффициентов канонических уравнений
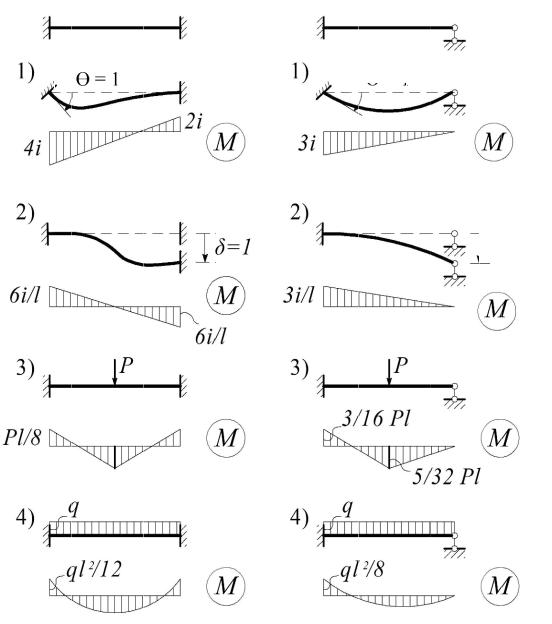
Чтобы определить коэффициенты и свободные члены системы (6.1) нужно предварительно найти эти реакции для отдельных стержней. Соответствующие
- 89 -
решения получаются интегрированием дифференциального уравнения изогнутой оси балки или с помощью метода сил и приведены на рис. 6.4, где через i = EJ/l
обозначена приведенная жесткость балки.
θ=1 |
θ =1 |
|
δ =1 |
δ =1 |
Рис. 6.4
С помощью этих стандартных решений нетрудно построить эпюры Mi0 и Mp0 в заданной раме. После этого для определения искомых реакций rij и Rip0 достаточно рассмотреть равновесие ее вырезанных узлов или других элементов, включающих введенные связи.
Пример 6.1. Построить эпюру изгибающих моментов Mp для рамы, рассмотренной в примере 4.3. (рис. 6.5, а).
