10380

- 10 -

СО – число опорных связей.

Как видим, при рассмотрении любой системы возможны три варианта:

1)W* > 0 – система заведомо подвижна;

2)W* = 0 – система имеет минимальное число связей, необходимых для

еенеизменяемости;

3)W* < 0 – система содержит избыточные связи.

На самом деле наше предположение о том, что в формуле (1.1) W* = W

неверно. Дело в том, что не всякая дополнительная связь уменьшает степень свободы системы – нетрудно представить связь, которая просто дублирует наложенную ранее, не меняя степени свободы системы.

Итак, условие W* 0 является необходимым, но недостаточным для образования неподвижной системы.

Если все-таки при условии W* < 0 система окажется неподвижной, то она одновременно будет и статически неопределимой, а число ее лишних связей можно найти по формуле:

Пример 1.1. Определить число лишних связей рамы (рис. 1.8).

Рис. 1.8

Решение. 1) Методом теоретической механики: общее число неизвестных реакций в опорах А, В, С и соединительном шарнире D равно восьми, максимально допустимое число уравнений для их определения – 6 (по три для каждого из дисков AD и DBC), число лишних связей Л = 8 – 6 = 2.

2) По формуле (1.2):

Для плоских ферм применять формулы (1.1) и (1.2) неудобно: если С – число стержней фермы, а У – число ее узлов, то во-первых будет слишком много дисков Д = С, а во-вторых почти все шарниры будут кратными.

- 11 -

Гораздо проще найти степень ее свободы из следующих соображений: каждый узел имеет две степени свободы, а каждый стержень как линейная связь, уменьшает общее число степеней свободы на единицу, откуда получим:

Пример 1.2. Определить степени свободы ферм (рис. 1.9).

P

Рис. 1.9

Решение. По формуле (1.3) находим:

–для схемы а): W* = 2 6 – 8 – 4 = 0;

–для схемы б): W* = 2 6 – 9 – 3 = 0.

Таким образом, необходимое условие неизменяемости выполняется для каждой из ферм, но только первая из них удет неподвижной. Система на рис. 1.9, б является изменяемой, и не может воспринимать показанную нагрузку, оставаясь в состоянии равновесия.

Примечания

1.Мы выяснили, что степень свободы зависит не только от того, какие элементы образуют систему, но и как они соединяются друг с другом. При неправильном образовании в одной части системы связи дублируют друг друга, а в другой – их недостаточно и система в целом оказывается изменяемой, как в примере на рис. 1.9, б. Вопрос о том, какие системы будут неподвижными, остается открытым.

2.Полезно рассмотреть еще одно определение.

Определение 1.3. Степень свободы системы W равна минимальному числу дополнительно введенных связей, превращающих ее в неизменяемую систему.

-12 -

1.2.3.Изменяемые системы

Ограничимся в дальнейшем рассмотрением систем, у которых условная степень свободы W* = 0.

Мы выяснили, что такие системы могут быть как изменяемыми, так и неизменяемыми, причем в последнем случае они будут статически определимыми. Для таких систем справедливо следующее определение.

Определение 1.4. Изменяемыми называются системы, которые получаются из неизменяемых систем при определенных критических значениях параметров.

Например, НС на рис. 1.10, а при = 0 переходит в ИС на рис. 1.10, б. Это сопровождается превращением статически определимой системы (СОС) в СНС, поскольку число линейно-независимых уравнений для определения опорных реакций уменьшается на единицу. При этом ранг матрицы этих уравнений становится равным двум, а ее определитель – равным нулю:

det A = 0.

Изменяемые системы (W > 0, W* = 0) подразделяются на:

–геометрически изменяемые системы (ГИС);

–мгновенно изменяемые системы (МИС).

Рис. 1.10

Мгновенно изменяемые отличаются от ГИС тем, что допускают не конечные – как рама на рис. 1.10, б, – а только бесконечно малые перемещения. При этом значения параметров, о которых идет речь в определении 1.4, у ГИС остаются постоянными, а у МИС – изменяются при перемещении.

Кроме того, переход неподвижных статически определимых систем в МИС может сопровождаться появлением бесконечно больших опорных реакций.

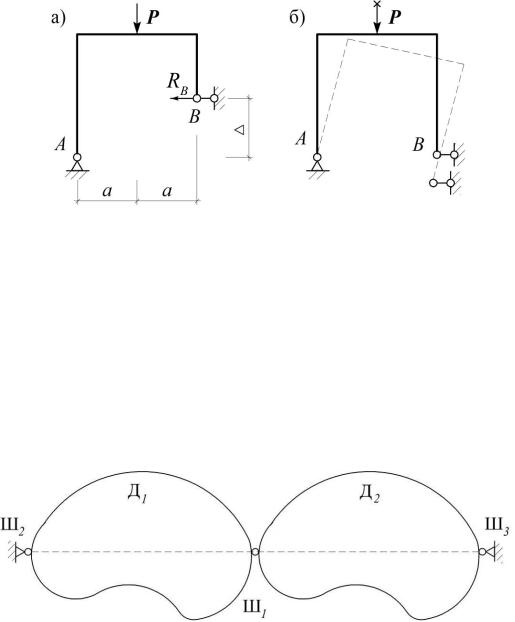
Рассмотрим, например, НС на рис. 1.11, а. Для определения опорной реакции RB составим уравнение равновесия: МА = 0, откуда найдем: RB = Pa/ .

Эта рама переходит в МИС на рис. 1.11, б при критическом значении параметра = 0. Нетрудно видеть, что предел RB при 0 равен бесконечности.

- 13 -

Это может привести к разрушению реальной конструкции, поэтому такие МИС не применяют в строительстве.

Термин «мгновенно изменяемая система», подчеркивает, что под действием приложенной нагрузки реальная деформируемая система может занять новую конфигурацию, для которой значение параметра станет отличным от критического. При этом в рассматриваемом примере (рис. 1.11, б) точка В сместится вниз и реакция RB примет конечное значение.

Рис. 1.11

Итак, мы выяснили, что принадлежность системы к классу МИС крайне нежелательна. Поэтому перечислим некоторые признаки МИС:

1)два диска, соединенные шарниром, связаны с остальной частью системы или с землей при помощи двух других шарниров, лежащих на одной прямой с первым (рис. 1.12);

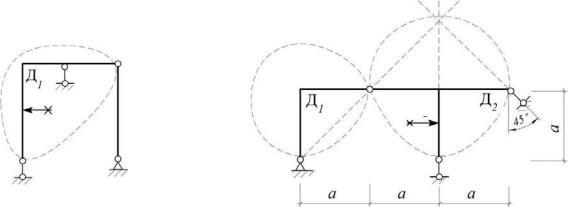
2)диск, прикреплен к системе или к земле при помощи трех линейных связей, у которых линии действия реакций параллельны (рис. 1.13) или пересекаются в одной точке (рис. 1.14).

Рис. 1.12

- 14 -

P

P

Примечания

1.МИС на рис. 1.11, б соответствует первому из приведенных признаков, роль второго диска выполняет подвижная опора В. Диск Д1 на рис. 1.14 выполняет роль третьей линейной связи по отношению к диску Д2.

2.Приведенные признаки МИС не являются исчерпывающими, и если исследуемая модель не отвечает им, то это не означает, что она не будет принадлежать к этому классу. Самым общим является аналитический метод исследования систем, основанный на рассмотрении уравнений равновесия для определения их опорных реакций.

3.Поскольку кинематический анализ связан с рассмотрением системы абсолютно твердых тел, он мог бы изучаться в курсе теоретической, а не как традиционно – строительной

механики. Кстати, в 7 на с. 26–28 можно найти две МИС, ошибочно включенных в задание, где требуется определить опорные реакции составной конструкции.

1.2.4. Способы образования и структурный анализ

Рассмотрим два способа образования стержневых систем, которые будут неизменяемыми и статически определимыми. Другими словами, выясним, при каких условиях соотношение:

будет не только необходимым, но и достаточным для образования таких систем.

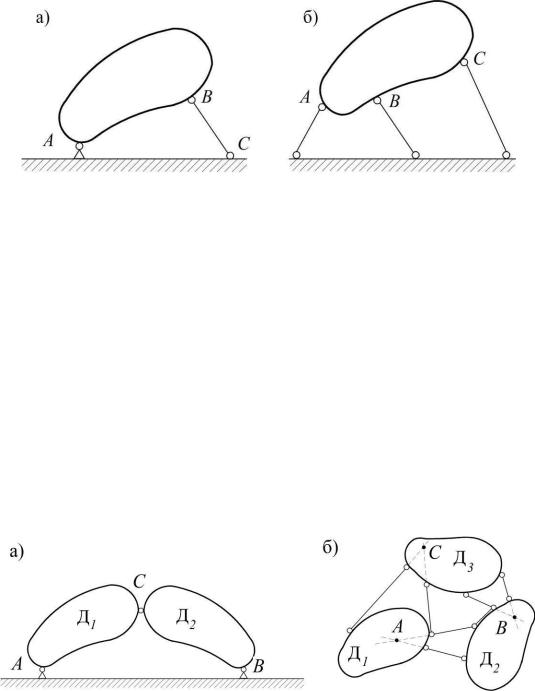
Соединение диска с землей (соединение двух дисков). Диск прикреплен к земле

при помощи шарнира и линейной связи, линия действия реакции которой не проходит через этот шарнир (рис. 1.15, а).

Шарнир А можно заменить двумя линейными связями, у которых линии действия реакций пересекаются в точке, через которую не должна проходить реакция третьей линейной связи (рис. 1.15, б).

- 15 -

Рис. 1.15

Если диск Д2 присоединяется не к земле, а к диску Д1, получим систему, которую можно принять за новый диск, имеющий ту же степень свободы, что и

диск Д1.

Этот способ образования систем называется диадным – от названия простейшей фермы, образованной из двух стержней, соединенных шарниром В. Роль первого стержня выполняет незагруженный диск АВ (рис. 1.15, а).

Соединение двух дисков с землей (соединение трех дисков). Два диска соедине-

ны друг с другом и с землей при помощи трех шарниров, не лежащих на одной прямой (рис. 1.16, а).

Аналогично соединяются три диска, при этом каждый шарнир можно заменить двумя линейными связями, у которых точки пересечения линий действия реакций также не должны лежать на одной прямой (рис. 1.16, б).

Рис. 1.16

Этот способ образования систем называется способом трехшарнирной арки. Очевидно, что он является более общим и сводится к диадному, если диски Д1 и Д2 незагружены и , значит, их можно заменить стержнями АС и ВС, соединенными в точке С (рис. 1.16, а).

Нетрудно заметить, что ограничения, налагаемые на способы образования системы, нужны для того, чтобы избежать появления МИС.

Структурный анализ. Суть такого анализа заключается в исследовании уже существующей системы с точки зрения возможности ее образования двумя рассмотренными способами.

- 16 -

При этом:

– системы, образованные из нескольких дисков, образуют один новый

диск;

–при условии (1.5) ни один из присоединенных дисков не должен иметь лишних связей;

–вновь образованная система будет неподвижной (НС) и статически определимой (СОС).

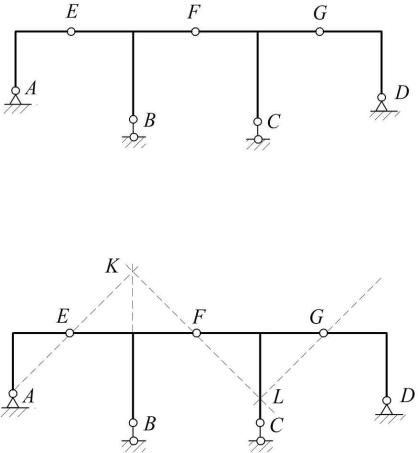
Пример 1.3. Выполнить структурный анализ рамы (рис. 1.17).

Рис. 1.17

Решение. Система состоит из пяти дисков, соединенных простыми шарнирами E, G, F и кратным шарниром D, эквивалентным двум простым.

Условная степень свободы по формуле (1.5):

W* = 3 5 2 5 5 = 0.

Диски Д1 и Д2 образуют по способу трехшарнирной арки новый диск Д1-2, жестко связанный с землей. К диску Д1-2 тем же способом при помощи шарнира D и линейной связи C присоединяется диск Д3, который образует новый и неподвижный относительно земли диск Д1-3. Наконец, к диску Д1-3 присоединяется диада Д4, Д5, образуя диск Д1-5. Таким образом, заданная система является СОС и НС.

Следует отметить, что системы могут быть образованы и другими способами – отличными от диадного и способа трехшарнирной арки, поэтому основанный на них структурный анализ не является универсальным методом исследования системы. Например, с его помощью нельзя дать ответ на вопрос об изменяемости рамы на рис. 1.18, поскольку ее нельзя образовать двумя указанными способами.

- 17 -

1.2.5. Аналитическое исследование системы

Как уже отмечалось, этот метод исследования систем является самым общим.

Суть метода. Уравнения равновесия для определения опорных реакций

где [A] – матрица коэффициентов при неизвестных;

{X} – вектор-столбец неизвестных опорных реакций; {B} – вектор-столбец нагрузки.

При этом для СОС любому вектору {B} однозначно соответствует единственный вектор {X}, что возможно только при условии: det [A] 0.

Учитывая, что в силу (1.5) СОС одновременно являются НС, можно сде-

лать вывод, что необходимым и достаточным условием неподвижной системы

будет:

Таким образом, для кинематического анализа системы достаточно вычислить определитель матрицы соответствующей системы алгебраических уравнений. Но можно избежать даже этой процедуры, учитывая некоторые сложности которые она вызывает уже при четвертом порядке определителя.

Метод нулевой нагрузки. Рассмотрим однородную систему уравнений, соответствующую (1.6):

Известно, что она имеет только нулевое решение, если det [A] 0, и наоборот – условием ненулевого решения будет: det [A] = 0.

Отсюда – следующее правило:

1)если система (1.9) имеет решение {X} = {0}, то соответствующая механическая система является неподвижной;

2)если система (1.9) имеет решение {X} {0}, то соответствующая механическая система является подвижной.

Пример 1.4. Выполнить кинематический анализ рамы (рис. 1.18).

Решение. Воспользуемся методом нулевой нагрузки, применив графический способ решения – см., например, [2], с. 53.

- 18 -

Из условия равновесия диска АЕ (рис. 1.19) следует, что реакции RA и RE направлены по прямой АЕ (аксиома 2).

Рис. 1.18

Рис. 1.19

Из условия равновесия диска EBF следует, что реакция RF проходит через точку K, где пересекаются линии действия R E = RE и RB (теорема о трех силах).

Из условия равновесия диска FCG аналогично находим линию действия реакции RG, проходящей вдоль прямой GL.

Наконец, рассмотрим диск DG . По аксиоме 2 реакция RG = RD должна быть направлена вдоль прямой GD, соединяющей точки их приложения. С другой стороны, R G = RG действует по прямой GL. Одновременно удовлетворить этим требованиям можно, лишь полагая RG = 0, откуда следует, что все реакции равны нулю, а значит {X} = {0} и система будет неподвижной.

Примечания

1.Подобно тому как СНС, которые мы рассмотрим в 4-й главе, могут быть статически неопределимыми внешним и внутренним образом, можно говорить о системах, изменяемых аналогично. Поэтому в общем случае вектор {X} в системе (1.6) должен содержать компоненты реакций не только внешних, но и внутренних связей.

2.Отметим, что в последнем примере 1.4 мы остаемся в рамках аналитического метода анализа геометрической изменяемости системы, несмотря на то, что при реализации метода

- 19 -

нулевой нагрузки применялся графический способ определения реакций связей. Такой прием вполне оправдан, поскольку формальный подход потребовал бы вычисления определителя двенадцатого порядка.

3.Анализ системы уравнений (1.6), независимо от условия (1.5), позволяет получить полную характеристику механической системы, в том числе степень ее свободы и степень ее статической неопределимости.

4.При построении модели сооружения ее параметры определяются с некоторой степенью точности, поэтому опасность на практике представляют не только МИС, но и близкие к

ним – у которых det [A] 0.

Математическая сторона основной задачи строительной механики основана на зависимостях, полученных в сопромате. Напомним их на примере напря- женно-деформированного состояния элемента рамы, для которого – в отличие от балки – поперечный изгиб сопровождается дополнительным растяжением или сжатием.

Пусть такой элемент длиной dx расположен в локальной системе координат Oxy, где ось Ox направлена по оси стержня, и загружен распределенной нагрузкой интенсивностью qx и qy вдоль Ox и Oy соответственно (рис. 1.20).

Напряженно-деформированное состояние стержня определяется девятью компонентами:

–внутренними усилиями (M, Q, N,);

–перемещениями (u, v, );

–деформациями (κ, , ).

Уравнения для определения этих функций можно разделить на три группы. Статические уравнения – связывают внутренние усилия (рис. 1.20, б) с за-

данной нагрузкой:

Геометрические уравнения – выражают деформации через перемещения, показанные на рис. 1.20, в, г:

Физические уравнения – представляют собой зависимости между внутренними усилиями и деформациями: