
10183
.pdf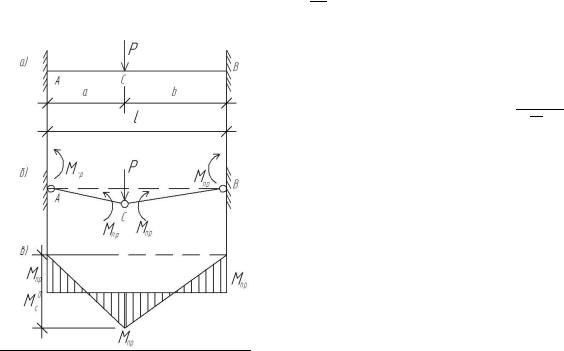
61
Балка, защемленная по концам
Предельное состояние для балки, защемленной по концам, определяется образованием трех пластических шарниров: двух в защемлениях и одного в пролете в месте наибольшего изгибающего момента (рис. 5.8).
Условие предельного состояния запишется в виде:
.
Полагая, что нагрузка изменяется пропорционально одному параметру P, за-
пишем, что |
|
. |
Тогда: .
Следовательно, предельная нагрузка для балки, защемленной по концам, всегда в два раза больше предельной нагрузки для простой статически определимой двухшарнирной балки при одинаковом их загружении и неучете влияния поперечной силы на образование пластических шарниров.
Рис. 5.8
Определение предельной нагрузки для многопролетных, неразрезных, статически неопределимых балок
Предельное состояние в неразрезной балке наступает тогда, когда число пластических шарниров на единицу превышает степень ее статической неопределимости, а также в том случае, когда в любом промежуточном пролете образуются три, а в крайних пролетах с шарнирной опорой - два пластических шарнира. Возможны и другие формы разрушения, например, когда одновременно обращаются в механизмы несколько или даже все пролеты неразрезной балки.
При расчете неразрезной балки, когда известны предельные несущие способности
всех ее сечений |
и требуется определить предельную нагрузку, поступают |
следующим образом:
- нагрузку на балку выражают через один общий параметр P, представляющий собой искомую величину (рис. 5.9);

62
- откладывают на опорах балки наименьшие значения предельных опорных моментов и проводят линии предельных опорных моментов;
- откладывают в каждом пролете балки значение предельного момента и проводят линии предельных пролетных моментов;
- к линии опорных моментов подвешивают эпюры изгибающих моментов от нагрузки для каждого пролета, рассматривая его как простую двухопорную балку. Эпюры подвешивают так, чтобы они каса-
Рис. 5.9 лись линий предельных пролетных моментов.
- исходя из предположения о возможном разрушении каждого пролета в отдельности, определяют параметры P для каждого пролета (P1, P2, P3 , где 1, 2, 3 … - номера пролетов) и из полученных значений выбирают наименьший параметр предельной нагрузки
Pmin .
Если неразрезная балка имеет все поперечные сечения с одинаковой несущей способностью (балка постоянного по всей длине сечения), то определение предельной нагрузки для нее производится путем выравнивания ординат эпюры предельных моментов.
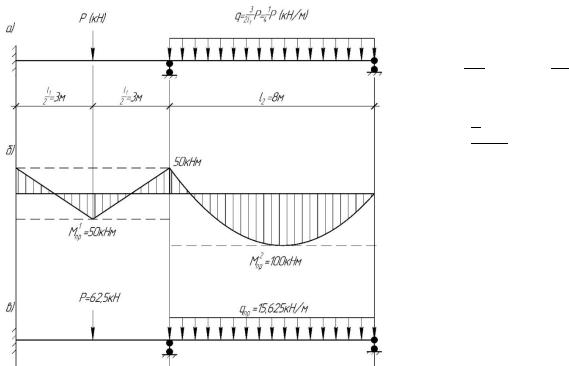
Пример |
|
|
Дано: неразрезная балка по рис. 5.10. |
|
|
Предельные моменты: - |
в первом пролете |
= 50 кНм; |
- |
во втором пролете |
= 100 кНм . |
Определить: предельную нагрузку для балки при заданной схеме ее загружения:
Предельная нагрузка в первом пролете будет (см. рис. 6.6
б):
,
откуда:
63
Предельная нагрузка во втором пролете:
или:
откуда:
По наименьшему параметру P = 62,5 кН устанавливаем предельную нагрузку на балку. Ее значения показаны на рис. 6.6 в .
Рис.5.10
Определение предельной нагрузки для статически неопределимых ферм
Предельной нагрузкой для фермы с n лишними стержнями считают ту нагрузку, при которой в (n+1) стержнях напряжения достигнут предела текучести . При этом условии система потеряет (n+1) связей и станет геометрически изменяемой.
В зависимости от того, какие (n+1) стержней из их общего числа “потекут”, может возникнуть значительное число различных механизмов, в которые способна превратиться ферма при исчерпании ее несущей способности. Очевидно, фактической формой разрушения будет та, при которой предельная нагрузка будет наименьшей. Трудоемкость решения задачи будет, прежде всего, заключаться в необходимости рассмотрения большого числа возможных схем разрушения.
Чаще оказывается более выгодным исследовать процесс постепенного возрастания нагрузки и проводить расчет системы в нескольких стадиях, рассматривая ее как упругую.
Составив для заданной фермы с n лишними неизвестными канонические уравнения метода сил и решив их, выявляют стержень с наибольшим напряжением, т.е. тот стержень, который потечет первым. Поскольку в последующей второй стадии усилие этого стержня остается неизменным, то его можно удалить, заменив усилием, равным произведению площади сечения удаленного стержня на предел текучести материала (
Затем рассматривают новую статически неопределимую ферму уже с (n-1) лишними неизвестными. Составив для нее канонические уравнения и решив их, выявляют следующий стержень, который должен потечь.
64
Проведя последовательно (n+1) таких расчетов, доходят до статически определимой системы, в которой возникновение предельного усилия в наиболее напряженном из оставшихся стержней приводит к превращению фермы в механизм и, следовательно, к ее разрушению.
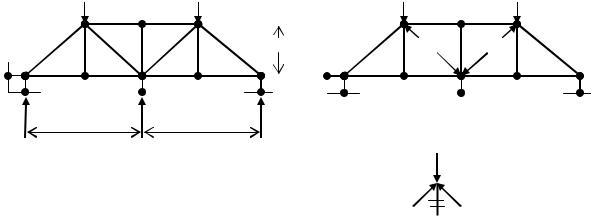
Применение изложенного метода рассмотрим на примере определения несущей способности двухпролетной статически неопределимой металлической фермы с одним лишним неизвестным при условии, что площади всех стержней одинаковы (рис. 5.11).
|
|
P |
|
|
P |
|
|
P |
|
|
P |
|||
a) |
O2 |
O3 |
|
|
|
|
б) |
O2 |
O3 |
|
||||
|
O1 |
D1 |
V2 D2 |
|
O4 3 м |
|
O1 |
|
|
V2 |
O4 |
|||
|
V1 |
|
|
|
V3 |
|
V1 |
|
|
|
|
V3 |
||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U1 |
U2 |
|
U3 |
|
U4 |
|
U1 |
U2 |
|
|
U3 |
U4 |
|
|
|
|
|
|
|
|||||||||
|
l = 8 м |
|
l = 8 м |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Pпр |
|
|
|
|
в)
Рис. 5.11
В связи с симметричностью фермы и нагрузки предельное состояние наступит тогда, когда потекут два стержня в каждой половине фермы. Для выявления стержней, которые потекут первыми, исследуем первую стадию работы фермы, рассматривая ее как упругую с одним лишним неизвестным. Составив каноническое уравнение, решив его и определив усилия всех стержней, находим, что наибольшие усилия возникают в стержнях
D1 и D2 (D1 = D2 = 1,654P) , следовательно, они потекут первыми. |
|
Исключив из системы стержни D1 и D2 , заменив их усилиями |
(рис. 6.7 б) и |
определив усилия, возникающие в стержнях во второй стадии работы фермы, найдем, что наибольшие по абсолютной величине усилия возникают в стержнях O1 и O4 , следовательно они потекут.
Рассматривая далее возникший механизм, из условия равновесия узла (рис. 6.7 в), спроектировав все действующие на него усилия на вертикальную ось, получим величину предельной нагрузки:
.

65
Определение предельной нагрузки для статически неопределимых рам
Предельное состояние n раз статически неопределимой рамы наступает в тот момент, когда в ней образуется (n+1) пластических шарниров. В результате образования пластических шарниров рама обращается в механизм, а , следовательно, полностью теряет свою несущую способность.
Сложность расчета статически неопределимых рам с учетом пластических свойств материала заключается в том, что трудно установить места, в которых будут образовываться пластические шарниры, так как их образование зависит от совместного действия внутренних усилий M, N и Q .
Известно, что условие предельного состояния сечения при изгибе с поперечной и продольной силами записывается в виде:
.
Влиянием поперечных сил обычно пренебрегают, поскольку оно незначительно. Тогда условие предельного состояния получает следующий вид:
.
Долю влияния продольных сил на образование пластического шарнира часто оценивают выражением:
Таким образом, расчет можно выполнять по следующему алгоритму: определяют предельную нагрузку для рам сначала без учета продольных сил, а затем устанавливают степень погрешности исходя из доли влияния продольных сил ( ) и вводят в расчет поправки, если в этом есть необходимость.
Более выгодным для определения предельной нагрузки статически неопределимых рам оказывается подход изучения постепенного возрастания нагрузки и расчета рамы в несколько этапов в упругой стадии. Поясним этот прием на примере.
66
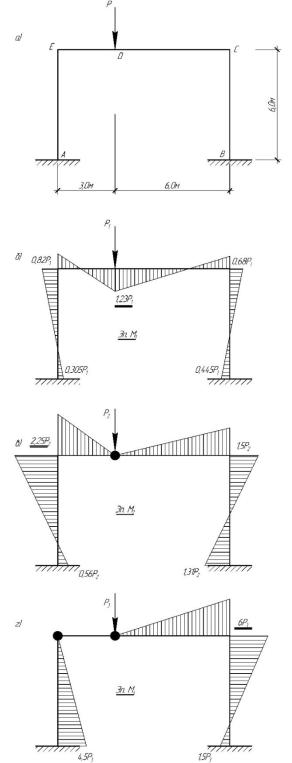
Рассмотрим три раза статически неопределимую раму по рис. 6.8а. При наличии трех лишних неизвестных потеря несущей способности должна произойти при образовании четырех пластических шарниров.
Производя статический упругий расчет рамы, получим эпюру изгибающих моментов M1, показанную на рис. 6.8б. По этой эпюре устанавливаем самое напряженное сечение с наибольшим изгибающим моментом (точка D), где образуется первый пластический шарнир. Расчетную нагрузку P1 определим из условия: Mпр = 1,23P1 , откуда
P1 = 0,813Mпр .
Вводим в сечение D пластический шарнир и рассматриваем вторую стадию работы рамы с двумя неизвестными (рис. 6.8в) под воздействием силы P2 (приращение нагрузки). Для этого случая строим эпюру моментов M2 , из которой легко установить, что наиболее напряженным является сечение E, т.е. в нем возникает второй пластический шарнир.
Приращение нагрузки P2 определяется из условия:
= |
, откуда |
|
. |
В раму, |
кроме шарнира D, вводим |
шарнир в сечение E и рассматриваем третью стадию работы рамы с одним лишним неизвестным.
Выполняем расчет от силы P3 (приращение нагрузки) и строим эпюру изгибающих моментов M3 . На основании этой эпюры устанавливаем, что третий пластический шарнир возникнет в сечении C.
Приращение нагрузки P3 определится из условия:
,
.
Рис.5.12.
Поскольку в рассматриваемой раме на одной прямой образовалось три пластических шарнира D, E и C, то система становится мгновенно-изменяемой, а ее несущая способность – исчерпанной.
Предельную нагрузку определим из условия, что несущая способность рамы:
= 0,813Mпр + + .
Расчетная эпюра изгибающих моментов в предельном состоянии, определяемая по формуле:
приведена на рис. 5.12.

67
6. ПРИБЛИЖЕННЫЕ МЕТОДЫ РАСЧЕТА СООРУЖЕНИЙ
Разработка приближенных методов расчета продиктована значительными масштабами проектирования рамных конструкций, используемых при строительстве зданий, мостов и целого ряда других сооружений.
Приближенные методы расчета необходимы, прежде всего, для установления размеров сечений элементов конструкций на этапе разработки эскизных проектов, а также при выполнении расчетов статически неопределимых систем, когда необходимо предварительно задаться жесткостями (или их соотношениями) всех элементов, входящих в расчетную схему. При отсутствии каких-либо аналоговых проектов проектируемому зданию или сооружению, размеры сечений элементов приходится определять, как правило, на основании приближенных расчетов.
6.1. Приближенные методы расчета неразрезных балок.
Моментные фокусные отношения и моментные фокусы.
Теория моментных фокусных отношений имеет большое практическое и теоретическое значение для расчета неразрезных балок и рам. Потребность в ее использовании возникает при рассмотрении эпюры изгибающих моментов, отвечающей загружению одного пролета балки.
Загрузив неразрезную балку нагрузкой, например, как показано на рис. 6.1 и составив и решив для этого случая систему уравнений трех моментов, мы получим вид эпюры моментов, изображенный на рис. 6.1. Характерной особенностью этой эпюры является то, что на каждом незагруженном пролете она имеет вид наклонной прямой с нулевой точкой в пределах пролета. Эти нулевые точки называются моментными фокусами. Их положе-
ния на рисунке обозначены F1, F2, F3, ,
В каждом пролете имеются два фокуса – левый и правый. Левым (правым) мо-
ментным фокусом какого-нибудь пролета называется нулевая точка эпюры моментов этого пролета при условии, что вся нагрузка на неразрезной балке расположена справа (слева) от него.
Рис. 6.1 Необходимо помнить, что не всякая нулевая точка какой либо эпюры моментов на-
зывается фокусом, а только та, которая получается на данном пролете при определенных условиях: когда на этом пролете нагрузка отсутствует, а вся она расположена по одну сторону от него. Например, нулевые точки в эпюре моментов в пролете 3-4 по рис. 6.1 не являются фокусами.
Достаточно просто доказать, что моментные фокусы обладают свойством инвариантности, т.е. на заданной неразрезной балке все фокусы занимают вполне определенное, не зависящее от внешней нагрузки, положение.
Рассмотрим, например, многопролетную неразрезную балку, у которой на первых четырех пролетах, считая слева, нет никакой нагрузки. Ту часть балки, которая расположена справа, можно отбросить, а ее действие на оставшуюся часть балки заменить моментом M, продольной силой N и поперечной силой Q, которые приложены к крайнему опорному сечению – рис. 6.2. Продольная сила, если она имеется, вызывает в балке только растягивающее или сжимающее усилие, но не влияет на эпюру изгибающих моментов
68
(если расчет выполняется по недеформированной схеме). Поскольку поперечная сила Q приложена на опоре, то она полностью воспринимается (уничтожается) сопротивлением самой опоры и дальше не передается. Следовательно, изгибающий момент в сечениях рассматриваемых пролетов балки возникает только от момента M, т.е. момент является единственной нагрузкой рассматриваемой части балки.
Зададимся вопросом: что произойдет с эпюрой изгибающих моментов, если в правой откинутой части балки произойдут какие-либо изменения: изменится характер, расположение или величина нагрузки, величина или количество пролетов, способ закрепления правого конца балки, изменятся как угодно поперечные сечения, поднимутся или опустятся те или иные опоры? От всех этих возможных вариаций, происходящих в правой части балки, изменится только величина (а может быть и знак) момента M. Можно считать, что этот момент умножится на какой-то множитель. Но в соответствии с принципом независимости действия сил, все ординаты эпюры изгибающих моментов также умножатся на тот же множитель. Следовательно, в тех точках, где ординаты равнялись нулю, они так и останутся равными нулю. Таким образом, положение в данном случае левых моментных фокусов останется прежним, что и требовалось доказать. То что мы доказали для левых фокусов в одинаковой мере справедливо и для правых фокусов.
Рис. 6.2
Из того факта, что фокусы занимают вполне определенные положения, следует ряд инвариантных отношений между величинами, характеризующими работу балки. Когда вся нагрузка расположена по одну сторону от данной группы пролетов, то на этих пролетах эпюра изгибающих моментов имеет вполне определенный вид. Следовательно, отношение между изгибающими моментами в двух произвольно взятых точках, расположенных на одном и том же пролете или на разных, остается постоянным.
Абсолютная величина отношения между изгибающими моментами на концах ка- кого-нибудь пролета называется моментным фокусным отношением.
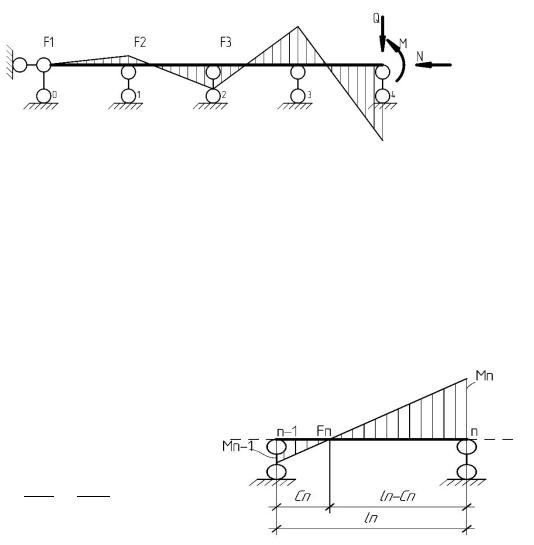
Различают левое и правое фокусные отношения, смотря по тому, определяется ли оно левым или правым фокусом. Например, для пролета ln по рис. 6.3 левым фокусным отношением называется величина:
(6.1)
Если известно положение фокуса, то известно и фокусное отношение, и наоборот.
Постоянным и независимым от нагрузки, расположенной по одну сторону от рассматриваемых пролетов, будет также и отношение между поперечными силами в двух сечениях, между углами поворота оси в двух сечениях, между прогибами, между опорными реакциями на двух опорах и т.д.
69
Каждое такое отношение может приобрести практическое значение, если его удастся использовать для расчета. Особое значение приобрели именно моментные фокусные отношения, которые мы и рассмотрим подробнее.
Когда нагрузка расположена справа от рассматриваемых пролетов, то положение левых фокусов определяется отношением:
; |
|
; . . . ; |
|
. |
|
|
Для опоры “n” по рис. 6.4 уравнение трех моментов будет иметь вид:
=0.
Если обе части уравнения разделить на Mn,, получим:
или:
.
Тогда:
Рис.6.4
В случае, если жесткости пролетов балки разные, полученное выражение примет следующий общий вид:
(6.2)
Полученная формула является рекуррентной, т.е. она позволяет переходить от «n” к “n+1”. Для того, чтобы воспользоваться этой формулой, необходимо определить хотя бы одно из фокусных отношений.
В балке с шарнирно опертыми концами левый фокус первого пролета совпадает с левым опорным сечением, так как момент на конце равен нулю. Поэтому:
.
В таком случае:
; |
|
|
|
, |
и т. д. |
|
|
Те же формулы справедливы и для балки, имеющей на левом конце консоль.
Если левый конец балки защемлен, то жесткая заделка моделируется тремя связями с дополнительным пролетом, приведенная длина которого l0 = 0 . В этом случае балка будет иметь шарнирно опертый левый конец и, следовательно, для пролета нулевой
длины k0 = . Тогда |
|
|
|
моментное фокусное отношение |
|
|
для фокуса, примыкающего к защемленному концу балки, всегда равно 2.

70
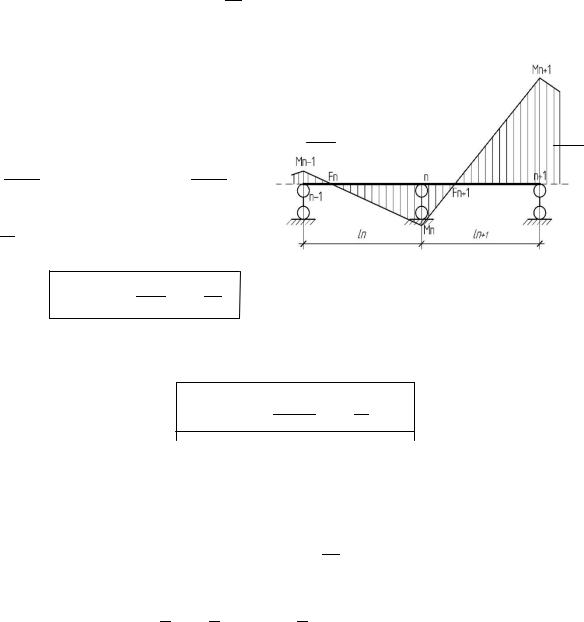
Аналогичный вид имеют формулы для правых фокусных отношений (рис. 6.5):
- для балок с равными жесткостями пролетов:
; |
|
- для балок с пролетами разной же- |
|
сткости: |
Рис. 6.5 |
|
(6.3)
Формулы 6.2 и 6.3 показывают, что положение левого (правого) фокуса любого пролета зависит только от приведенной длины (при разных жесткостях пролетов) самого пролета и всех лежащих слева (справа) от него, но совершенно не зависит от величин, характеризующих остальные пролеты балки.
Из формул также следует, что фокусные отношения являются положительными числами, которые могут принимать всевозможные значения от низшего предела, равного 2, до высшего, который равен бесконечности.
Зная фокусные отношения, можно графически строить эпюры моментов – фокусы получаются при этом на чертеже сами собой. Можно также построить фокусы независимо от эпюры моментов, так как из пропорции (6.1) получается следующее выражение для расстояния левого фокуса от ближайшей левой опоры (рис 6.3):
Аналогичный вид имеет формула для правого фокуса (рис.6.5):
Если левый конец балки защемлен, то фокусное отношение k1=2, следовательно
т.е. фокус, примыкающий к защемленному концу балки, отстоит от него на расстоянии, равном одной трети длины соответствующего пролета. Это – наибольшее возможное для фокусов расстояние от ближайшей опоры; наименьшее возможное расстояние равно нулю.
Между левыми и правыми фокусными отношениями существуют зависимости, которые могут использоваться для проверки числовых значений этих отношений.
Для m-пролетной балки с шарнирно опертыми концами и с сечениями, постоянными на протяжении каждого пролета, зависимость между фокусными отношениями имеет вид:
.
