
10183
.pdf
51
4.5. Седловидные напряженные сетки
Покрытие седловидными сетками применяется для постоянных зданий и временных сооружений. Примером постоянного здания с таким покрытием может служить Ре- лей-арена в США (рис. 8.13), возведенная в 1953 г. и давшая мощный толчок развитию висячих покрытий. В качестве других сооружений можно отметить Дворец культуры и спорта в Варне и, как пример временного сооружения – покрытие Олимпийского стадиона в Мюнхене.
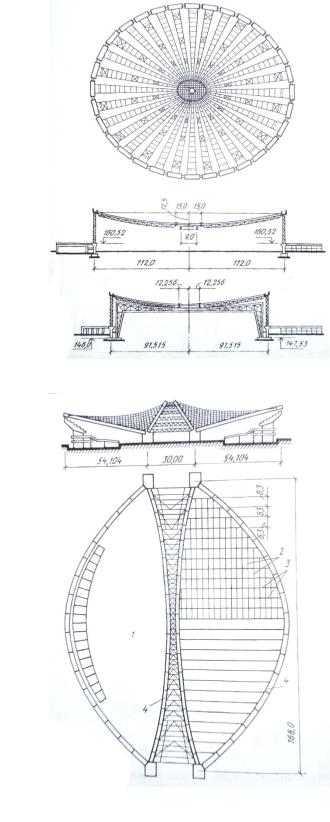
Рис. 4.10
1 – железобетонные арки;
2 – несущие тросы;
3 – стабилизирующие тросы.
от конструкции кровли. В легких сооружениях, покрытых брезентом, оно не должно превышать 1,0 м во избежание образования больших водяных мешков.
Форма плана может быть самой разнообразной, но чаще всего сетку закрепляют на две наклонные параболические арки или опорное кольцо сложной конфигурации, которые и воспринимают тяжение сетки покрытия.
Приближенный расчет напряженной сетки, имеющей форму гипара и закрепленной в недеформируемом опорном контуре, на действие внешней равномерно распределенной по покрытию нагрузки ведут аналогично двухпоясным системам исходя из пропорционального распределения нагрузки между несущими и стабилизирующими тросами по всему покрытию.
52
4.6. Металлические оболочки-мембраны
В покрытиях висячих систем широкое применение получили тонкостенные металлические оболочки-мембраны. Мембранами называют тонкие оболочки, в работе
которых изгибными напряжениями можно пренебречь.
Главными преимуществами этих систем являются совмещение несущей и ограждающей функции и индустриальность изготовления. Утеплитель и гидроизоляцию кровли в таких системах укладывают непосредственно на несущую оболочку, не применяя никаких кровельных плит.
Изготовленные на заводе полотнища оболочки доставляют на строительство в виде рулонов, из которых на месте собирают всю оболочку без применения лесов.
Примерами таких покрытий могут служить Олимпийский стадион (рис. 4.11) и велотрек (рис. 4.12), построенные в Москве.
Конструкция покрытия стадиона (рис. 4.11) включает гибкие радиальные фермы, опирающиеся на периферийное опорное
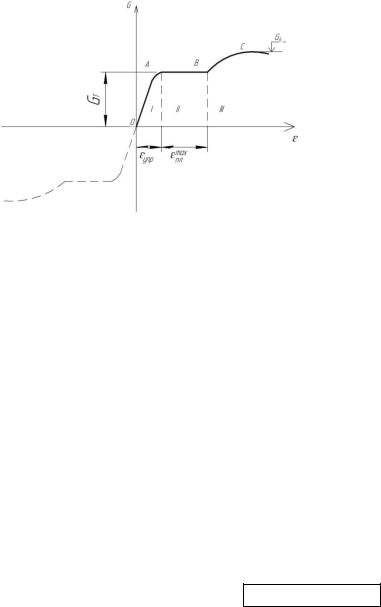
Рис. 4.11
Рис. 4.12
1 – металлическая мембрана; 2, 3 – элементы постели; 4 – металлические арки
кольцо и одновременно служащие “постелью” для укладки полотнищ чашеобразной оболочки. Полотнища оболочки скрепляются между собой и с радиальными фермами высокопрочными болтами. В готовом покрытие фермы работают совместно с оболочкой, значительно увеличивая ее жесткость, особенно при действии неравномерных нагрузок.
Покрытие велотрека (рис. 8.15) выполнено с помощью двух металлических мембран отрицательной гауссовой кривизны. Каждая из мембран прикреплена к двум металлическим аркам коробчатого сечения, а “постелью” для укладки и скрепления между собой полотнищ мембраны служат металлические полосы, провисающие вниз, и перпендикулярно им расположенные гнутые швеллеры, выгнутые вверх. Рулоны мембраны раскатывались по выверенной сетке “постели” и приваривались к ней.
Форма оболочек покрытия может быть самой разнообразной: цилиндрической, конической, сферической, чашеобразной, седловидной, шатровой и др. Работа их под нагрузкой отличается, но пространственность работы, присущая всем формам оболочек,
53
делает их работу выгодной в сравнении с другими видами покрытий и позволяет применять листы толщиной от 2 до 5 мм.
Вдоль толщины оболочек напряжения и деформации могут считаться постоянными. В этом случае говорят о безмоментной оболочке. При изменении напряжений и деформаций по толщине оболочки, например, по линейному закону, оболочку называют моментной – при ее расчете учитываются изгибающие и крутящие моменты.
При расчете в оболочке выделяют срединную поверхность, проведенную через середины толщин оболочки. К срединной поверхности обычно относят все уравнения оболочки.
В безмоментной теории оболочек предполагают, что равнодействующие напряжений действуют в срединной поверхности. При этом оболочка не оказывает сопротивления изгибу и кручению. В плоскостях, касательных к срединной поверхности оболочки, возникают внутренние силы, которые называют мембранными усилиями. В каждой точке срединной поверхности они образуют симметричный двумерный тензор с составляющими:
, |
, |
где:
- толщина оболочки; , , - составляющие тензора напряжений, действующих в плоскости,
касательной к срединной поверхности и отнесенных к координатам 1, 2 на этой поверхности.
Для трех составляющих внутренних сил безмоментного напряженного состояния N1 , N2 , S12 можно составить два уравнения равновесия в плоскости, касательной к срединной поверхности оболочки, и одно уравнение равновесия в направлении нормали к этой поверхности. Отсюда следует, что безмоментная оболочка является внутренне статически определимой.
В моментной теории оболочек учитываются линейные составляющие функций изменения напряжений по толщине оболочки.
Существование безмоментного напряженного состояния в оболочке связано с необходимостью соблюдения целого ряда условий, касающихся закрепления контура и характера действующих нагрузок. В реальных конструкциях соблюдение этих условий затруднительно, поэтому на этапе рабочего проектирования расчет выполняют по моментной теории. Однако на стадии эскизного проектирования и предпроектных предложений используют расчет по безмоментной теории, так как он позволяет сравнительно быстро и просто выполнить расчет для большого числа вариантов оболочек
54
5. Расчет конструкций с учетом пластических свойств материала на основе метода предельного равновесия
5.1. Особенности расчета стержневых систем по предельному состоянию
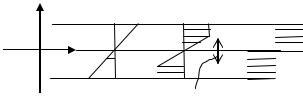
Диаграмма зависимости напряжений от деформаций достаточно пластичных материалов, какими, например, являются стали обычной прочности, как известно, имеет вид, показанный на рис. 5.1. Участок OA диаграммы отвечает упругой стадии деформирования (I), зависимость между напряжениями и деформациями здесь подчиняются закону Гука: . Горизонтальный участок AB описыванет пластическую стадию дефор-
мирования (II), в которой , E = 0. Кривая BC отвечает III стадии нагружения
– стадии упрочнения материала. Она завершается разрушением образца при напряжении , называемым временным сопротивлением.
Для практических расчетов реальную диаграмму заменяют идеализированной диаграммой Прандтля, которая отвечает
Рис. 5.1
идеальному упруго-пластическому материалу.
В 1938 году профессор А. А. Гвоздев, основываясь на упрощенной диаграмме работы материала, предложил особый метод определения предельной несущей способности. Идея метода состоит в том, что работа конструкции рассматривается в момент, непосредственно предшествующий ее разрушению, когда еще выполняются условия равновесия для внутренних и внешних сил, достигших предельных значений. Именно по этой причине и возникло название метода – метод предельного состояния (или равновесия).
5.2. Условия предельного состояния при разных видах деформации системы
Условия предельного состояния при ЦРС
Для пластичных материалов предельное состояние сечения при центральном растяжении или сжатии наступает в том случае, когда во всех волокнах поперечного сечения элемента напряжения достигнут предельной величины, равной . В этом случае:
- для растянутых стержней :
- для центрально сжатых стержней ( |
|
- коэффициент продольного изгиба): |
||
|
||||
|
|
|
|
|
|
|
|
|
|
55
Условия предельного состояния при чистом изгибе
Предельное состояние сечения элемента при чистом изгибе наступает в тот момент, когда напряжения во всех волокнах по высоте достигнут предельной величины, рав-
ной |
|
(рис. 5.2) и эпюра нормальных напряжений примет вид двух прямоугольников в |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сжатой и растянутой зонах с ординатами, |
|
Y |
Aс |
|
|
|
равными |
. Рассмотренное состояние для |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поперечного сечения будет соответство- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
вать образованию в нем пластического |
|||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
MТ |
|
|
|
|
|
M |
пр |
шарнира. |
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пластический шарнир является односто- |
|
Aр |
|
|
|
|
|
|
|
|
|
|
|
|
|
упругое |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ронним, |
т.е. допускает поворот только в |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ядро |
пластический |
сторону увеличения деформаций (в сторо- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шарнир |
||||
|
|
|
|
|
|
|
Рис. 5.2 |
|
|
|
ну раскрытия), в противном случае он |
||||||||||||
“замыкается”.
Исходя из условий равновесия для рассматриваемого по рис. 5.2 сечения в стадии развития пластического шарнира можно записать:
Из первого выражения получаем или . Это указывает на то, что нулевая линия в сечении с пластическим шарниром совпадает с центральной осью и делит сечение на две равные части.
Из |
второго выражения |
следует, что |
, |
где: |
- статический момент половины площади поперечного сечения относи- |
||
тельно центральной оси; |
- пластический момент сопротивления площади попе- |
||
речного сечения. |
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
Для прямоугольного сечения (bxh) |
|
, тогда |
|
|
|
. Известно, что уп- |
|
|
|
||||||
ругий момент сопротивления для того же сечения равен |
|
. Отношение |
к |
||||
|
|||||||
показывает, во сколько раз предельный момент |
|
больше упругого момента MТ , соот- |
|||||
ветствующего фибровой текучести. |
|
|
|
|
|
|
|
Это отношение составляет:
- для прямоугольного сечения - 1,5;
-для круглого сечения - 1,7;
-для двутаврового сечения - (1,15 – 1,17).

56
Условия предельного состояния при изгибе с поперечной силой
Очевидно, что величина предельного момента при наличии поперечной силы будет меньше, чем при чистом изгибе.
Приближенное решение задачи основано на предположении, что касательные напряжения, возникающие в сечении, будут восприниматься только упругим ядром сечения. В этом случае
Рис. 5.3
предельное состояние наступит в тот момент, когда касательные напряжения на уровне нейтрального слоя достигнут своих максимальных значений.
Из курса сопротивления материалов известно, что максимальные касательные на-
пряжения определяются по формуле: |
|
|
|
|
|
|
|
|
|
|
, откуда: |
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Тогда, предельный момент запишется в следующем виде: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
Таким образом, условие предельного состояния сечения при изгибе с поперечной силой примет следующий окончательный вид:
Условия предельного состояния при изгибе с продольной силой
При одновременном статическом действии изгибающего момента и продольной силы (растягивающей или сжимающей) на элемент, выполненной из углеродистой стали или стали повышенной прочности, предельное состояние по прочности определяется образованием шарнира пластичности. Развитие пластических деформаций при наличии
момента и продольной силы так же, как и при чистом изгибе, приводит к образованию шарнира пластичности, но при этом положение нейтральной оси сечения в процессе развития пластических
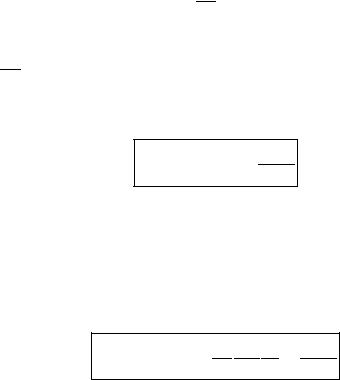
Рис. 5.4
деформаций смещается. При увеличении
момента и продольной силы на одной из сторон стержня фибровые напряжения достигают предела текучести и затем останавливаются в своем развитии; эпюра становится притупленной (рис. 5.4). Напряжения в прочих фибрах, так же как и кривизна стержня (угол наклонной части эпюры напряжений) продолжают расти, пока напряжения на другой сторо-
57
не стержня тоже не достигнут предела текучести. После этого пластичность распростра-
няется на все фибры сечения. |
|
|
Очевидно, что разность площадей эпюр напряжений, умноженная на |
, равна |
|
предельной продольной силе ( |
т.е. |
|
|
, или так: |
|
откуда: |
|
. |
|
|
|
|
|
||
Принимая во внимание, что при чистом изгибе |
и |
, выраже- |
||
ние предельного момента может быть записано в следующем виде: |
|
|||
|
= |
, |
или так: |
|
а, учитывая выражение для |
: |
.
Для прямоугольного поперечного сечения:
, |
|
, тогда: |
|
. |
|
|
Окончательно получаем условие предельного состояния сечения при изгибе с продольной силой:
Условия предельного состояния при изгибе с поперечной и продольной силами
Исходя из рассмотренных выше случаев, условие предельного состояния сечения при одновременном действии изгибающего момента, поперечной и продольной сил запишется в следующем виде:
Таким образом, все ранее рассмотренные решения являются частным случаем полученного общего выражения.

58
5.3. Определение предельных нагрузок для различных систем
Плоские статически определимые фермы
Предельное состояние для плоской статически определимой фермы наступает в тот момент, когда в одном из ее стержней напряжение достигает предела текучести , в результате чего этот стержень неограниченно деформируется при постоянном усилии и ферма обращается в механизм, который не в состоянии воспринимать дальнейшее увеличение нагруз-
, в результате чего этот стержень неограниченно деформируется при постоянном усилии и ферма обращается в механизм, который не в состоянии воспринимать дальнейшее увеличение нагруз-
ки.
|
|
|
Исходя из условий предельного со- |
|
|
стояния сечения при центральном рас- |
|
|
|
тяжении – сжатии можно записать: |
|
|
Рис. 5.5. |
|
|
- |
для растянутых стержней : |
|
; |
|
|||
- |
для сжатых стержней : |
|
. |
|
|||
Поскольку нагрузка, действующая на систему, изменяется всегда пропорционально |
|||
одному параметру, то справедлива запись: |
|
пр . P , где пр - продольные усилия в |
|
стержнях фермы от нагрузки при параметре P=1.
Будем иметь: |
пр , |
тогда: |
- для растянутых стержней: |
пр ; |
|
- для сжатых стержней: |
|
пр . |
Таким образом, определение предельной нагрузки для плоской статически определимой фермы сводится к следующему:
- определяют усилия во всех стержнях заданной фермы от нагрузки при параметре
P = 1;
-определяют параметры P для каждого стержня в отдельности: сжатый стержень; растянутый стержень;
-по наименьшему параметру из полученных устанавливают предельную нагрузку для заданной фермы.
Статически определимые балки
Предельное состояние для статически определимой балки наступает в тот момент, когда в одном из ее сечений образуется пластический шарнир. Появление пластического шарнира в каком-то сечении балки соответствует моменту перехода балки в механизм, не способному сопротивляться дальнейшему возрастанию нагрузки.
Условие предельного состояния сечения балки при изгибе с поперечной силой имеет вид:
.
Обозначая |
, где |
, получим: |
.
|
|
|
|
|
|
|
|
|
59 |
|
|
Помножив левую и правую части полученного равенства на |
|
, придем к квад- |
|||||||
|
|
|||||||||
ратному уравнению следующего вида: |
|
|
|
|||||||
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
решая которое определим значение предельного напряжения |
, а затем и предельную |
|||||||||
нагрузку для заданной балки. |
|
|
|
|||||||
|
В практических расчетах обычно пренебрегают влиянием поперечной силы, пола- |
|||||||||
гая |
, так как влияние поперечной силы в большинстве случаев незначительное. В |
|||||||||
этом случае предельную нагрузку для статически определимых балок устанавливают исходя из предельного условия:
.
Полагая, что нагрузка, действующая на балку, изменяется пропорционально одному параметру P, можно записать, что пр . P , где пр – изгибающий момент от заданной нагрузки при параметре P=1 , откуда получаем:
= |
|
|
|
. |
|
|
Полученное выражение, таким образом, определяет предельную нагрузку для статически определимой балки при возникновении пластического шарнира в сечении с наибольшим значением изгибающего момента.
Однопролетные статически неопределимые балки
Определение предельных нагрузок для простейших статически неопределимых балок будем выполнять без учета поперечной силы, поскольку, в большинстве случаев, влияние ее незначительно, но в то же время учет поперечной силы сильно осложняет расчет. При этом следует иметь в виду, что полученные без учета поперечной силы величины предельных нагрузок будут иметь несколько завышенные значения.
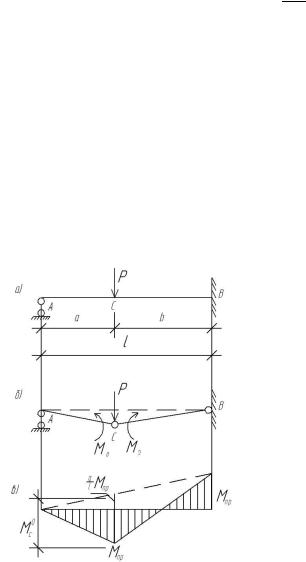
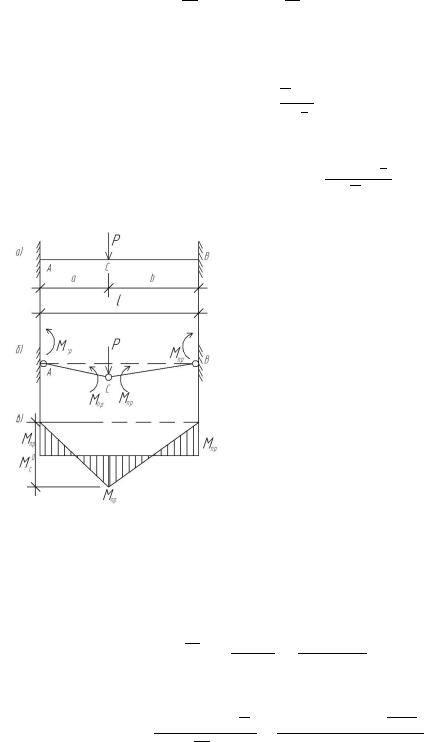
5.3.1. Балка, защемленная с одной стороны и шарнирно опертая с другой Предельное состояние таких балок наступает в тот момент, когда образуются два
|
пластических |
шарнира: один в пролете с |
|||||
|
раскрытием вниз, другой в защемлении с |
||||||
|
раскрытием вверх (рис. 5.6).. |
||||||
|
В результате образования двух пласти- |
||||||
|
ческих шарниров балка обращается в меха- |
||||||
|
низм, который не в состоянии восприни- |
||||||
|
мать дальнейшее увеличение нагрузки, т.е. |
||||||
|
балка теряет свою несущую способность. |
||||||
|
Принимая во внимание одновременное |
||||||
|
образование пластических шарниров в бал- |
||||||
|
ке, можем записать: |
||||||
|
откуда: |
|
|
|
|
|
, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|||||
|
|
|
|
|
|
||
|
Условие |
предельного состояния без |
|||||
|
учета поперечной силы запишется в сле- |
||||||
Рис. 5.6 |
дующем виде: |
|
|
|
|
|
|
|
|
|
|
60 |
|
|
. |
|
|
|
|
|||
|
|
|
|
|
Полученное условие при замене |
на |
|||
расчетное сопротивление материала |
|
|||
(например, для стали) может быть использовано для определения предельной расчетной нагрузки.
Полагая, что нагрузка на балке изменяется пропорционально одному параметру P,
можно написать: , где: - изгибающий момент в основной системе (двух шарнирной статически определимой балке) от нагрузки при параметре P = 1.
Тогда условие предельного состояния примет вид:
,
откуда предельная нагрузка для балки при рассмотренном виде ее загружения:
.
Пример
Дано:
-пролет балки l = 6,0 м;
-материал балки – сталь обычной прочности
типа С245 по ГОСТ 27772-88, для которой = Ry =
=240 мПа (24 кН/см2);
-пластический момент сопротивления сече-
ния балки: |
; |
-схема загружения балки – по рис. 6.3;
-влиянием собственного веса балки и поперечной силы в расчете пренебречь.
Рис. 5.7 |
|
Определить: |
|
- предельную нагрузку |
. |
Решение:
- максимальный (в сечение под силой) изгибающий момент в основной системе при параметре P=1:
;
- предельная нагрузка для балки при принятой схеме загружения составит:
Ответ: предельная нагрузка для рассматриваемой балки составляет =131,3 кН
