Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4629 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Нижегородский Государственный Архитектурно-Строительный Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

10075

.pdf
Скачиваний:
0
Добавлен:
25.11.2023
Размер:
3.88 Mб
Скачать
☆

справедливости основной гипотезы по закону Фишера – Снедекора со степенями

свободы nx, ny.

 

S 2

 

 

 

 

 

 

 

 

 

 

 

 

 

K

max

Fn

 

 

k

 

k

 

F

( , n

 

, n

 

)

2

,n

y

nabl

kr

xx

y

 

x

 

 

 

obr

 

 

 

 

Smin

 

 

 

 

 

 

 

 

 

 

 

 

 

поскольку К>1, то критическая область односторонняя с права Проверим теперь гипотезу о равенстве математических ожиданий у наблюдаемых

случайных величин Н0={ах=ау} при условии равенства их дисперсии { х2= у2}. В ка-

честве критерия примем величину К, распределенную при условии справедливости

основной гипотезы по закону Стьюдента с nх+ nу -2 степенями свободы.

K

 

 

 

 

 

X ñð Yñð

 

 

 

nx ny (nx

ny

2)

 

tn n 2

 

 

 

 

 

 

 

 

 

 

nx

ny

 

 

(n

 

1)S 2 (n 1)S 2

 

 

 

 

 

 

 

 

x y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

x

 

y

y

 

 

 

 

 

 

 

 

knab

 

kkr

tobr

( / 2, nx

ny 2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

Критическая область гипотезы (Область где проверяемая гипотеза отвергается) здесь двухсторонняя и симметричная .

U m {yˆ(x, 1 , 2 ,.. m )}
М ( ) 0
Y (X )

♥♠2.6 Корреляция двух величин

Две случайные величины X и Y могут быть независимыми между собой, зависимыми строго функционально или зависимыми статистически. При статистической зависимости между случайными величинами распределение одной из величин зависит

от того,

какое значение имеет другая случайная величина. Степень статистической за-

висимости величин X и Y характеризует теоретический коэффициент корреляции

Пирсона

 

 

 

 

 

 

 

XY

M ( X

Y ) M ( X )

M (Y )

,

 

 

 

 

 

 

 

 

 

 

D( X ) D(Y )

обладающий следующими свойствами:

 

 

 

 

1)

его значение по модулю не превышает единицы 1 ХУ 1.

2)

для независимых величин X и Y

 

ХУ 0 ,

3)

для линейно зависимых величин

ХУ 1.

Сама статистическая зависимость описывается функциями условного распределения, например, для непрерывных случайных величин функциями плотности условного

распределения f X (x y) или f y ( y x) . Однако нахождение этих функций и их практиче-

ское использование обычно затруднено и малоэффективно. Чаще статистическая зависимость рассматривается в более простом виде, в виде функциональной зависимости числовых характеристик одной из величин от значения другой величины. Такая зависи-

мость называется корреляционной и описывается функциями регрессии

ˆ

или

ˆ

Y (x)

X ( y) .

Так например, наиболее часто используется регрессия в форме условного математического ожидания:

ˆ

M (Y х) yf y ( y x)dy Y (x) .

y

Корреляционная зависимость приближает статистическую зависимость функциональной зависимостью и имеет следующий вид:

ˆ

Y Y (x) .

Здесь Y - объясняемая переменная, x - значение объясняющей переменной X , а - случайная величина ошибки (невязки) корреляции с нулевым математическим ожиданием при любом значении х.

Дисперсия же ошибки D( ) не нулевая, но при «хорошей» функции регрессии она не должна быть большой, и не должна зависеть от переменной х. Построение таких функций регрессии является задачей регрессионного анализа.

Для приближенного построения функции регрессии будем искать наилучшее в определенном, но довольно широком, m-параметрическом классе функций

таким образом, что бы дисперсия ошибки

D( , 1 , 2 ,.. m ) --- min

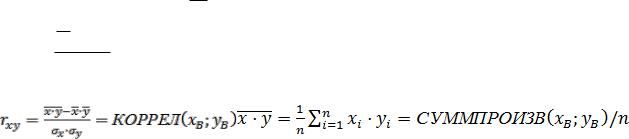
как функция от параметров k была минимальной. Такое приближение называет-

ся среднеквадратической регрессией в классе U m . Для приближенного построения функции регрессии можно так же воспользоваться данными наблюдений за величинами

X и Y, полученными в выборке

(хi , yi ) объема n. Такие оценки для функции регрессии

уˆ(x) ищутся так же в кассе

U m , имеют минимальное суммарное отклонение от

наблюдаемых значений yi , строятся методом наименьших квадратов и называются выборочной среднеквадратической регрессией.

2.4.1Линейная среднеквадратическая регрессия

Линейная регрессия является простейшей регрессионной моделью, согласно которой функция регрессии является линейной 2-х параметрической функцией:

уˆ(x) а вх ,

где а, в - неопределенные коэффициенты, которые оценим по наблюдаемым данным. Пусть имеется двухфакторная выборка n наблюдений (хi , yi ) за величинами

X и Y , которую будем называть корреляционным полем.

Помимо выборочных

средних значений х, у и выборочных дисперсий Dx 2x ,

Dy 2y , вычислим так

же среднее произведение xy и выборочный (эмпирический) коэффициент корреля-

ции rxy xy x y , который является выборочным аналогом теоретического коэффи-

x y

циента корреляции Пирсона XY .

Построим

коэффициенты

а, в методом наименьших квадратов. Для этого найдем

такие значения

а, в , которые

минимизируют

сумму

квадратов

отклонения yi и

yˆi yˆ(xi ) , то есть

ошибки ei yi

yˆi

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

n

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ei2 ( yi

yˆi )2

( yi

a bxi

)2 min .

 

 

 

 

 

 

 

 

 

 

 

 

 

i 1

i 1

 

 

i 1

 

 

 

 

 

 

a,b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Из необходимых условий минимума найдем искомые значения а, в :

 

 

 

 

 

 

 

 

 

 

n

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ei2 2 ( yi a bxi ) 0 ;

y а вх ; a y вх ,

 

 

 

 

 

 

 

 

 

 

a i 1

i 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

xy

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xy

 

 

 

 

 

 

 

 

 

 

 

аx вх 2 ; в

 

 

 

ei2 2 ( yi

a bxi )xi 0 ;

xy

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

b i 1

i 1

 

 

 

 

 

 

 

 

 

 

 

 

x 2 x 2

Через выборочный коэффициент корреляции

rxy , коэффициент в

 

представим в

форме в r

y

,

 

а уравнение выборочной линейной среднеквадратической регрессии

 

 

xy x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

имеет одну из следующих форм:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ˆ

 

 

 

ˆ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y(x) а вх ;

y(x) y в(х x) ;

 

 

 

 

ˆ

y

 

yˆ(x) y

 

(x x)

 

y(x) y rxy

x

(х x) ;

y

rxy

x

.

 

 

 

 

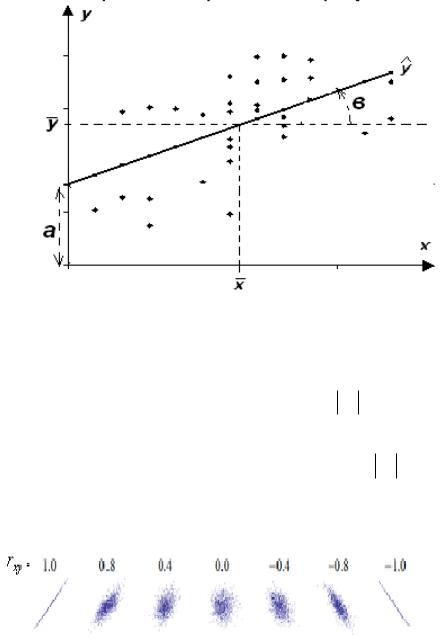
Построенная выборочная линейная среднеквадратичная регрессия является простейшим приближение корреляционной зависимости, показывает тенденцию (тренд) этой зависимости и изображается прямой на корреляционном поле, наименее уклоня-

ющейся от его точек. Прямая линия

ˆ

регрессии y(x) а вх проходит через точку

(х, у), отсекает от оси х отрезок а ,

и имеет угол наклона с тангенсом равным в , как

это изображено на рис. 15.1.

 

Рис. 15.1 Прямая линейной среднеквадратической регрессии

Выборочный коэффициент корреляции rxy характеризует степень корреляционной зависимости наблюдаемых величин Х и У и обладает следующими свойствами:

1)его значения по модулю не превышают единицы ( rxy 1),

2)для независимых Х и У коэффициент близок к нулю (rxy 0) ,

3)для линейно зависимых величин он близок к единице ( rxy 1) .

Геометрически он показывает «тесноту» корреляционного поля возле прямой линии регрессии, что иллюстрирует рис. 15.2 для различных значений коэффициента.

.

Рис. 15.2 Корреляционное поле для различных уровней корреляции величин

Из рис. 15.2 видно, что некоррелированной выборке (rxy 0) соответствует не-

ориентированное шаровое корреляционное поле, с ростом rxy поле сжимается и ориен-

тируется к прямой линии регрессии. Знак коэффициента говорит о нарастающем или убывающем тренде зависимости.

 

 

 

 

 

 

 

ˆ

имеют нулевое среднее значение е 0 , так как

 

 

 

 

Ошибки регрессии ei yi yi

y yˆ ,

и минимальную в соответствии с методом наименьших квадратов дисперсию

 

 

1

 

n

 

 

De

 

 

ei2

Dy (1 rxy2 ) , так называемую остаточную дисперсию, которая тем меньше,

 

 

 

 

 

 

 

n i 1

 

 

чем выше коэффициент корреляции. Величина выборочной дисперсии De является статистической оценкой для дисперсии ошибки D( ) , однако, это смещенная оценка. Не-

смещенной (исправленной)

оценкой является

 

 

величина S 2

n

 

D ,

величина

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n 2

e

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S (

 

 

ei2 )1/ 2 называется стандартной ошибкой регрессии. Ошибки для коэффици-

n

 

 

 

 

 

2 i 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ентов регрессии вычисляются по формулам:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Sb2

 

S 2

, Sa2

 

 

x 2 S 2

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n Dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n Dx

 

 

 

 

 

В

корреляционном анализе

также

 

вводится

понятие коэффициента

детерминации

R 2

DY / DY , показывающего долю объясненной части дисперсии,

объясняемой пере-

менной Y. Поскольку Dy Dyˆ

De , то коэффициент детерминации представим так же в

следующем виде:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R 2 1

De

rxy2 ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

D y

 

 

 

 

 

 

 

 

 

 

показывающем его прямую связь с коэффициентом корреляции.

 

 

 

 

 

 

 

Известно [9] распределение случайных величин, связанных с введенными выше

коэффициентами при условии независимости величин

X и Y :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

rxy

 

 

n 2

 

tn 2 ~ распределение Стьюдента с n 2 степенями свободы,

 

 

 

 

 

 

 

 

 

 

 

 

1 r 2

 

 

 

 

 

xy

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R 2 (n 2)

 

F1,n 2 ~ F-распределение Фишера с 1 1, 2

n 2 степенями свободы.

 

1 R

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Эти величины используется для построения критериев значимости выборочных коэффициентов rxy и R 2 , и их распределение приводится приложениях 3 и 5 соответствен-

но.

Действительно, например, задаваясь уровнем значимости проверяемой гипотезы

H 0

{ XY 0} , соответствующей

независимости величин Х и Y, можно сравнить

наблюдаемое значение критерия

tnab с критическим значением tkr ( ) . Если

tnab tkr ( ) , то гипотеза принимается, что говорит о незначимости выборочного ко-

эффициента корреляции, мало отличного от нуля. Если же tnab tkr ( ) , то гипотеза

отвергается, то есть выборочный коэффициент корреляции, а значит и уравнение регрессии, значимы. Значимость коэффициента корреляции говорит о том, что полученный по данной выборке коэффициент неслучайно отличен от нуля, а корреляционная зависимость между наблюдаемыми величинами существенна.

Аналогично строится критерий Фишера для проверки гипотезы H 0 {R 2 0} о значимости коэффициента детерминации R 2 :

если Fnab Fkr ( ) , то гипотеза H 0 принимается, т.е. R 2 незначим. Выводы критериев значимости rxy и R 2 идентичны [9].

Значимость коэффициентов регрессии может быть оценена по критериям Стью-

дента

a

tn 2 ,

b

tn 2 .

 

 

 

Sa

Sb

Построенная регрессия может быть использована для прогноза значения Y для людого значения Х.

Ошибка прогнозирования зависит от удаления величины х от среднего:

Доверительный интервал для прогнозируемого значения Y Y Y cтроится

исходя из распределения Стьюдента для отклонения прогнозируемого значения от истиннго по заданной надежности:

3. Многомерные статистические данные

Измерительные данные, с которыми работает инженер-исследователь или аналитик в процессах проектирования, производства, эксплуатации и мониторинга различных технических, экологических, социально-экономических систем редко бывают одномерными. Обычно при исследовании объекта или множества объектов измеряется несколько параметров объекта. Таким образом формируется многомерный статистический набор данных. При строительстве и эксплуатации зданий и сооружений могут быть измерены и запротоколированы множество различных параметров (рис. 3.1).

Рис. 3.1. Факторы влияния на здание

Измеряемые величины в большинстве случаев являются случайными как по своей природе, так и за счёт ошибок измерения

x x0 δx x ,

где x0 - истинное или среднее значение величины, δx - флуктуация измеряемой величины, x - ошибка измерительного прибора и измеряющего субъекта. Виды изме-

рений разнообразны и классифицируются по множеству признаков (рис. 3.2).

Рис. 3.2.Виды измерений

Приведём несколько примеров наборов статистических данных, как документально оформленных измерений.

Многомерность статистических данных состоит в том, что у каждого наблюдаемого объекта Ai ( X1, X2 , X3 ,..., X m ) , измеряется (фиксируется) несколько величин-

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности