
9845
.pdf
имеющую отставание по фазе на угол 90° от приложенной силы. Говорят, что эта компонента находится в квадратуре с возбуждением.
На рисунке 1.2 векторы ОА и ОВ показывают соответственно вещественную и мнимую компоненты смещения в плоскости Арганда. Вектор ОС является общим смещением с амплитудой, определяемой выражением
{
 Re2 (x) + Im 2 (x)} и равной:
Re2 (x) + Im 2 (x)} и равной:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Fe jωt |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
(1.9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
||||
|
|
|
ω |
|
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|||
|
1 |
- |
ω |
|
|
|
|
+ 2ξ ω |
ω |
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Общее смещение отстает от вектора силы на угол θ, определяемый выра-
жением tan −1
Im(x) |
и равный: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Re(x) |
|
|
|
|
|
|
||
|
θ = tan −1 |
2ξ ω |
ω0 |
|
. |
(1.10) |
||
|
|
ω |
|
|
2 |
|||
|
|
|
|
|
|
|||
|
1 - |
|
ω0 |
|
|
|
||
|
|
|
|
|
|
|
||
Поэтому для установившегося состояния решение уравнения (1.2) колебаний может быть записано в виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Fe j(ωt −θ ) |
|
|||
x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
, |
(1.11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
ω |
|
|
2 |
|
2 |
|
|
|
|
2 |
|
k |
|
|||
|
1 |
- |
ω |
|
|
|
|
+ 2ξ ω |
ω |
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Где угол θ определяется равенством (1.10).
10

Рис.1.2. Вещественная и мнимая компоненты смещения по отношению к вектору силы
Величина в квадратных скобках выражения (1.11) является модулем комплексной частотной характеристики H(ω) (смотри равенства (1.4) и 1.5). Она назы-
вается коэффициентом усиления и является безразмерным отношением между амплитудой смещения X и статическим смещением F k .
1.2. Характеристики виброзащитной системы
На рис. 1.3,а представлен модуль комплексной функции частотной харак-
теристики в зависимости от безразмерного отношения частот ω |
ω |
для различ- |
|
0 |
|
|
|
ных значений относительного демпфирования. Видно, что увеличение относительного демпфирования приводит к уменьшению амплитуд и смещению пи-
ков влево от вертикальной линии, проходящей через ω |
ω |
= 1 . Пики соответст- |
|
0 |
|
|
|
|
11 |
|
|

вуют частотам, определяемым из выражения:
ω = ω0 |
|
, |
|
(1 − 2ξ 2 ) |
(1.12) |
а значение пика H(ω) равно:
H(ω) |
|
= |
|
1 |
|
. |
(1.13) |
|
|
|
|
||||||
|
|
|
|
|
||||
|
2ξ |
1 − ξ 2 |
||||||
|
|
|
|
|
|
|||
Рис.1.3,а. Коэффициент усиления H(ω) в зависимости от безразмерного отношения частот
ω ω0 для различных значений относительного демпфирования ξ
12

Рис.1.3,б. Отставание по фазе смещения по отношению к силе в зависимости от
ω ω0 для различных значений ξ
Для слабого демпфирования (ξ<0,05), кривые почти симметричны относитель-
но вертикальной линии, проходящей через точку ω |
ω |
0 |
= 1 . Значение пика |
|
H(ω) |
|
|
||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
находится в непосредственной близости от точки ω |
ω |
= 1 и равно |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H(ω) |
|
|
1 |
= Q , |
|
|
|
|
(1.14) |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где величина Q называется добротностью. |
|
|
|
|
|
|
|
|
|
|
|||||||||
Для кривой с относительным демпфированием ξ = 0,1 , например , точки P1 и Р2, |
|||||||||||||||||||
для который амплитуда |
|
H(ω) |
|
уменьшается до значения Q |
|
от пиковой вели- |
|||||||||||||
|
|
||||||||||||||||||
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чины, называются точками половинной мощности. (Если ордината отложена в логарифмическом масштабе, то Р1 и Р2 являются точками, амплитуды которых H(ω) уменьшаются на 3 дБ и поэтому называются -3 дБ точками). Разница в
частотам между точками Р1 и Р2 называется 3 дБ: шириной полосы частот системы и для слабого демпфирования можно показать, что:
ω =ω2 ω1 = 2ξω0 , |
(1.15) |
где ω = 3 дБ - ширина полосы частот, ω1 - частота, соответствующая точке Р1, ω2 -частота, соответствующая точке Р2.
Из уравнений (1.14) и (1.15) получим:
13

ω2 − ω1 |
= 2 |
c |
= |
1 |
= η , |
(1.16) |
ω0 |
|
|
||||
|
cc |
|
Q |
|
||
η - называется коэффициентом потерь.
На рис. 1.3,б представлены кривые фазового угла θ в зависимости от отношения
ω ω0 для различных значений ξ , построенных на основании выражения (1.10).
Следует отметить, что все кривые проходят точку θ = π  = 1 , другими словами, независимо от величины демпфирования фазовый угол между силой и
= 1 , другими словами, независимо от величины демпфирования фазовый угол между силой и
смещением на собственной частоте колебаний без демпфирования ω′ = ω0 |
ра- |
|||
вен 90°. Кроме того, фазовый угол стремится к нулю при ω |
ω |
→ 0 и к 180° |
при |
|
|
|
0 |
|
|
|
|
|
|
|
ω ω |
→ ∞ . |
|
|
|
|
0 |
|
|
|
Для рассмотрения изменений синфазной компоненты Re(х) и компоненты в
квадратуре Im(x) смещения уравнений (1.7) и (1.8) вычерчены на графике в за- |
||
висимости от отношения ω |
ω |
и представлены соответственно на рисунках |
|
0 |
|
|
|
|
1.4,а и 1.4,б. Кривые вещественной компоненты смещения на рисунке 1.4,а
имеют нулевое значение при ω |
ω |
= 1 независимо от демпфирования и имеют |
|||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пик и спад на частотах: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
= ω |
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 − 2ξ |
|
|
|||||||
|
|
|
|
|
|
|
|
|
, |
(1.17) |
|||
|
|
ω |
|
= ω |
|
|
|
|
|
|
|||
|
|
2 |
0 |
|
|
1 + 2ξ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
соответственно.
С уменьшением демпфирования (значение ξ становится меньше) пик и спад возрастают по величине и приближаются друг к другу. В пределе, когда ξ=0,
график имеет асимптоту при ω ω0 = 1 . Частоты ω1 и ω2 часто используются для определения демпфирования системы с помощью выражения:
|
ω |
2 ω |
|
2 |
− 1 |
|
|
|
|
|
|
|
|||
η = 2ξ = |
|
1 |
|
|
|
. |
(1.18) |
ω |
|
|
2 |
|
|||
|
2 ω |
+ 1 |
|
||||
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
Кривые мнимой компоненты смещения имеют спад в непосредственной близо-
14

сти точки ω |
ω |
= 1 и выглядят острее, чем кривые для |
|
H(ω) |
|
, показанные на |
|
|
|||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
рис. 1.3а при соответствующих значениях ξ. |
||||||
Рис.1.4,а. Вещественная компонента смещения в зависимости от безразмерного отношения
частот ω ω |
для различных значений ξ |
|
0 |
Рис.1.4,б. Мнимая компонента смещения в зависимости от ω ω |
для различных |
|
0 |
значений ξ
Если вещественную и мнимую компоненты, а также отношение частот
15

вычертить на графике в системе трех взаимно перпендикулярных осей, получим трехмерную кривую, показанную на рис. 1.5.
Штриховая линия представляет собой кривую при ξ=0 и полностью лежит в плоскости {Re(x),ω}. Кривые, показанные на рис. 1.4,а и 1.4,б, в действи-
тельности являются проекциями кривых, подобных представленным на рис. 1.5 в плоскости {Re(x),ω} и {Im(x),ω}соответственно. Третья проекция кривой на плоскость [Re (х), Im(х)] выглядит подобно кривым, показанным на рис. 1.6.
Рис.1.5. Трехмерный график вещественной и мнимой компонент смещения в зависимости от частоты
16
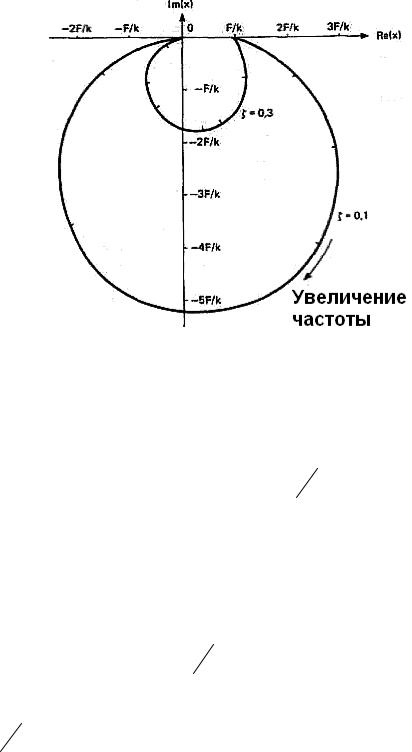
Рис.1.6. Комплексный график вещественной компоненты в зависимости от мнимой компоненты при изменении частоты дли различных значений ξ
Правые части уравнений (1.7) и (1.8) вычерчены в осях X и У на рис. 1.6 соот-
ветственно для различных значений отношения ω ω0 . Представлены две кривые
для ξ=0,1 и ξ=0,3. Эти кривые также можно получить, вычерчивая общее смещение, определяемое выражением (1.9), от начала координат под углом θ относительно Re(x), определяемым выражением (1.10). Таким образом, кривая на рис. 1.6 является годографом общего смещения для определенного значения ξ в
зависимости от отношения частот ω |
ω |
. Из рис. 1.6 также видно, что независи- |
|
0 |
|
|
|
мо от величины демпфировании на собственной частоте колебаний без демп-
фирования ω ω0 = 1 вещественная компонента равна нулю, иными словами, фа-
зовый угол между силой и общим смещением составляет 90°.
1.3. Линейное гистерезисное демпфирование
Другим видом демпфирования, нейным демпфированием и дающим цессам демпфирования на практике,
позволяющим записать уравнение с лидостаточно хорошее приближение к проявляется гистерезисное (иногда называе-
17

мое структурным) демпфирование. Большое количество материалов, находящихся под действием циклического нагружения (для деформаций ниже предела упругости), проявляют связь между напряжением и деформацией, характеризуемую петлей гистерезиса. Энергия, рассеиваемая за один цикл колебания вследствие внутреннего трения в материале, пропорциональна площади петли гистерезиса, и поэтому процесс называется гистерезисным демпфированием. Считаем, что внутренние трение не зависит от скорости деформирования (следовательно, и от частоты) и в достаточно большом диапазоне пропорционально смещению. Таким образом, демпфирующая сила пропорциональна упругой силе, но поскольку энергия рассеивается, то она должна быть в фазе со скоростью (в квадратуре со смещением).
Таким образом, для простого гармонического движения демпфирующая сила равна:
jγkx = γk |
x′ |
, |
(1.19) |
|
ω |
||||
|
|
|
где γ называется коэффициентом структурного демпфирования. Уравнение движения системы с одной степенью свободы и гистерезисным демпфированием можно, следовательно, записать в виде:
mx¢¢ + |
γk |
x¢ + kx = Fe jωt , |
(1.20) |
|
|||
|
ω |
|
|
или |
|
|
|
mx¢¢ + k(1 + jγ )x = Fe jωt , |
(1.21) |
||
где k(1+ jγ ) называется комплексной жесткостью.
Решение уравнения (1.21) для установившегося состояния представим в виде:
|
|
|
|
|
1 |
|
|
|
|
Fe jωt |
|
|||
|
jωt |
|
|
|
|
|
|
|
|
|||||
x = Xe |
|
= |
|
|
|
|
|
|
|
|
× |
|
, |
(1.22) |
|
|
- (ω |
|
|
2 |
+ jγ |
|
|||||||
|
|
|
1 |
ω |
) |
|
|
|
k |
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
соответствующем уравнению (1.4) для случая вязкого демпфирования. Умножая числитель и знаменатель в квадратных скобках на комплексное сопряженное знаменателю выражение, можно получить вещественную и мнимую компоненты смещения:
18

|
|
|
|
ω |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jωt |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jγ |
|
|
|
|
|
|
|
|
|
|
|
Fe |
|
|
|||||||
|
|
|
|
|
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(1.23) |
||||||||||
x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
k |
|||||||||||||||
|
|
|
|
|
+ γ |
2 |
|
|
|
|
|
|
- |
ω |
|
|
|
|
|
|
|
+ |
γ |
2 |
|
|
|
||||||||||||||||||||||
|
1 - |
ω |
ω |
|
|
|
|
|
|
|
|
|
|
1 |
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Следовательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jωt |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fe |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
(1.24) |
||||||||||||||
|
Re(x) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
+ γ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
1 |
- |
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- jγ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fe jωt |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Im(x) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
. |
|
|
|
|
|
|
|
|
(1.25) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
+ γ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 - |
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Общее смещение, равное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fe jωt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
(1.26) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
ω |
|
|
|
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 - |
ω |
|
|
|
|
|
+ γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
отстает от вектора силы на угол, равный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
θ = tan |
−1 |
|
|
|
|
|
|
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(1.27) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
- |
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Выражение (1.27), представляющее угол θ, вычерчено на графике в зависимости от отношения ω ω0 для различных значений γ и показано на рис. 1.7. Вид-
ω0 для различных значений γ и показано на рис. 1.7. Вид-
но, что кривые на рис. 1.7 подобны кривым рисунка 1.3,б для вязкого демпфирования, однако есть некоторые незначительные отличия. Для очень низких значений ω ω0 отклик для гистерезисного демпфирования зависит от величины γ и фазовый угол θ (рис. 1.7) стремится к величине tan-1γ, тогда как он равен нулю при вязком демпфировании. На рис. 1.8 представлен комплексный гра-
ω0 отклик для гистерезисного демпфирования зависит от величины γ и фазовый угол θ (рис. 1.7) стремится к величине tan-1γ, тогда как он равен нулю при вязком демпфировании. На рис. 1.8 представлен комплексный гра-
19
