9845

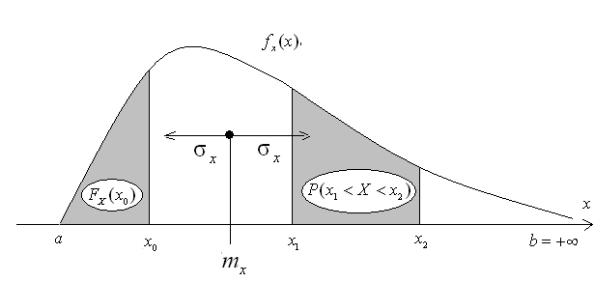
x2

P(x1 < X < x2 ) = FX (x2 ) − FX (x1 ) = ∫ fx (x)dx ,

x

которые иллюстрируются на рис.8.1.

Рис. 8.1. Иллюстрация закона распределения случайной величины и ее основных числовых характеристик

Функции распределения или плотности распределения при исследованиях часто не известны и предполагаются гипотетической моделью явления, кроме того, они часто являются избыточной информацией. Обычно в инженерных расчетах и оценках достаточно знать некоторые основные числовые характеристики случайных величин, таковыми являются два первых начальных момента и второй центральный момент:

D[ X ] = Dx = ∫ (x − mx )2 fx (x)dx; Dx = mx2 − mx2 .

Ωx

Эти величины есть постоянные (неслучайные) числовые величины и они час-

120

тично дают представление о распределении. Величина mx называется математическим ожиданием (МО) и характеризует средневзвешенное значение случайной величины. Дисперсией Dx является второй центральный момент и она характеризует средний разброс значении СВ около своего центра. Действительно, если - отклонение СВ от своего центра, то:

Dx = M [ Xɶ 2 ] = mx2 − mx2 .

Дисперсия имеет размерность квадрата случайной величины, поэтому удобно ввести величину σx = Dx , называемую средним квадратическим отклонени-

ем (СКО) случайной величины. Смысловое значение математического ожидания и СКО так же иллюстрируются на рис. 8.1. Математическое ожидание и дисперсия случайной величины обладают следующими свойствами:

M [ X + Y ] = M [ X ] + M [Y ] , M [ Xɶ] = 0 ,

M [α] = α , M [αX ] = αM [ X ] , α = const .

D[α] = 0 , D[αX ] = α2 D[ X ]

Используя эти свойства, любую случайную величину Х можно привести к

В качестве примеров приведем некоторые случайные величины, которые достаточно часто применяются для описания случайных явлений.

- Равномерная СВ Х=Rn(a,b):

- Релеевская СВ Х=Re(σ):

и ряд других величин [133], но самой известной и широко используемой является нормальная случайная величина Х=N(m,σ):

ность нормальной величины состоит в том, что согласно центральной теореме закона больших чисел чем сложнее случайная величина, чем больше случайных факторов влияет на ее значение, тем ближе она к нормальной величине

[131].

Когда в опыте по наблюдению за случайным явлением наблюдаются сразу две или несколько случайных величин, то оказывается недостаточно знать распределение и характеристики каждой наблюдаемой СВ. Дело в том, что случайные величины могут быть полностью независимыми или статистически зависимыми. Статистическая зависимость случайных величин имеет место, когда распределение одной случайной величины зависит от того, какие значения принимает другая величина.

Пусть имеются две случайные величины Х1 и Х2 со своими распределениями, но они статистически зависимы. Тогда их распределения могут быть описаны через функции совместного распределения или функции условного распределения f X1 (x1 x2 ), f X 2 (x2 x1 ) . В качестве числовой характеристи-

ки степени зависимости случайных величин вводится корреляционный момент:

K12 = cov( X1 , X 2 ) = M [ Xɶ1 × Xɶ2 ] = M [ X1 × X 2 ] - M [ X1 ]× M [ X 2 ] .

122

Для его вычисления необходимо знать совместное распределение СВ, но известно, что ковариационный момент обладает свойствами:

Вводится безразмерная нормированная ковариация (коэффициент корреляции):

причем для него всегда выполняется -1 £ R12 £ 1 . Если в опыте одновременно наблюдается несколько случайных величин Х1 , Х2 ,…, Хn, то вводятся симметричные матрицы ковариационных моментов Кij или коэффициентов корреляции Rij :

Для вычисления характеристик случайных величин необходимо знать их законы распределения, а для вычисления ковариаций еще и совместные распределения, что как отмечалось выше сложно, а то и избыточно.

Для оценки этих теоретических характеристик можно воспользоваться статистическим набором наблюдательных данных за этой величиной или несколькими величинами. Эти наблюдения, объединяются в выборку опреде-

123

ленного объема n:

xV = {x1 , x2 ,..., xn } = {xi ;i =1, n} .

Выборка должна иметь достаточный объем для получения надежных оценок характеристик случайной величины и не искажать пропорции самой величины, что возможно, например, при случайном отборе наблюдений (измерений). По выборке можно построить ее основные характеристики (моменты), такие как:

x = 1 ∑n xi - выборочное среднее,

n i=1

Dx = (xi - x )2 = 1 ∑n (xi - x )2 - выборочная дисперсия,

n i=1

σx = Dx - выборочное СКО.

При одновременном наблюдении за двумя и более случайными величинами

получаются многофакторные выборки xV = {xi, j ; j = 1, m; i = 1, n}, по которым

можно построить выборочные ковариации k jk и коэффициенты корреляции

Построенные выборочные характеристики являются случайными величинами, так как получены по результату случайного выбора наблюдений. Это серьезно отличает их от их теоретических аналогов математического ожидания mx , дисперсии Dx и др. характеристик, являющихся постоянными вели-

чинами. Вопрос об их близости, то есть качестве оценок mx » x , Dx » Dx ,

R12 » R12 и других, подробно рассматривается в теории статистических оценок.

124

Здесь только отметим, что величина

называется несмещенной (исправленной) дисперсией, а величина Sx несмещенным СКО, или стандартом выборки. Ее введение связано с тем, что именно ее математическое ожидание совпадает с теоретической дисперсией M [Sx2 ] = Dx , поэтому оценка Dx ≈ Sx2 является несмещенной, как и оценка mx ≈ x , и именно они будут использоваться далее в статистических расчетах.

8.2. Случайные процессы в анализе вибрации

Наблюдая за случайной величиной, мы предполагали ее неизменность при наблюдениях в различные моменты времени. Если случайное явление таково, что его характеристики изменяются с течением времени, то говорят о случайном процессе. Если наблюдается случайный процесс X(t), то в каждый момент t0, t1,…t n,.. мы наблюдаем случайные величины Х0, Х1,… Хn,.. со своими распределениями и числовыми характеристиками. При наблюдении за процессом в целом мы получим его реализацию в виде некоторой неслучайной функции х(t). Таким образом, временным срезом (сечением) случайного процесса является случайная величина, а его реализациями - набор неслучайных функций [119]. Случайный процесс и его связь с мгновенными случайными величинами и неслучайными реализациями иллюстрируется на рис.8.2.

125

Рис.8.2. Иллюстрация случайного процесса, его реализаций xi(t) и сечений Xj в моменты tj

Закон распределения для случайного процесса X(t) может быть описан через функции распределения и плотности распределения:

Числовые же характеристики случайного процесса являются неслучайными функциями времени:

M [ X (t)] = mx (t) = ∫ x × fx (x, t)dx; M [ X 2 (t)] = mx2 (t) = ∫ x2 × fx (x, t)dx ,

Ωx Ωx

D[ X (t)] = Dx (t) = ∫ (x - mx (t))2 × fx (x, t)dx; Dx (t) = mx2 (t) - mx2 (t) ,

Ωx

σx (t) = Dx (t) .

Их смысловое значение аналогично значениям характеристик случайной величины и иллюстрируется на рис.8.2.

126

Случайный процесс помимо введенных функций характеризуется корреляционной функцией, которая показывает корреляционную зависимость между временными сечениями случайного процесса:

Здесь - центрированный случайный процесс с нулевым ма-

тематическим ожиданием, а R(t, t') - нормированная корреляционная функция.

Корреляционные функции имеют следующие важные свойства:

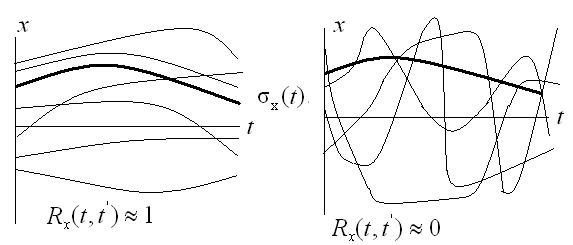
Смысл корреляционной функции иллюстрирует рис. 8.3, на котором изображены процессы с высокой корреляцией и с малой корреляцией. Видим, что при примерно одинаковом математическом ожидании и приблизительно равной дисперсии характер случайных процессов резко отличается.

Рис.8.3. Иллюстрация случайных процессов с различными корреляционными функциями

Мы рассматриваем случайный процесс с непрерывными состояниями и непрерывным временем, если же процесс дискретен по времени, то он описывается системой случайных величин X(tj), а вместо корреляционной функции рассматривается корреляционная матрица: K jk = cov( X (t j ), X (tk )) .

127

Если процесс наблюдается только в некоторые дискретные моменты, то име-

ется статистическая выборка xV = {t j , xi, j ; j = 1, m; i = 1, n} , по которой может быть построена выборочная корреляционная матрица k jk или

Рассмотрим примеры случайных процессов, параметрами которых являются нормальная случайная величина X=N(m,σ) и константы m, σ, α, ω. Такие процессы будем называть элементарными случайными процессами (ЭСП). Вычислим характеристики этих процессов, используя свойства математического ожидания и дисперсии [119]. Рассматриваемые процессы приведены на рис.8.4.

Рис.8.4. Элементарные случайные процессы с X=N(m,σ), α,ω=const

Пример 1. ЭСП Y (t) = α×t + X линейный процесс со случайным началом.

Пример 2. ЭСП Y (t) = X ×t + α линейный процесс со случайным наклоном

Пример 3. ЭСП Y (t) = X ×e−αt - затухание со случайным началом.

Пример 4. ЭСП Y (t) = X ×sin(ωt + α) - гармонический процесс со случайной ам-

плитудой.

y

Если случайный процесс проходит однородно во времени и инвариантен к сдвигу по времени, то его называют стационарным. Например, такие процессы, как входное напряжение прибора от сети, шум от автомагистрали, давление газа в трубопроводе и другие процессы не зависят от момента времени.

129