
9709
.pdf
22
Напомним, что при выводе уравнений Навье-Стокса были сделаны следующие предположения:
1)жидкость несжимаема,
2)напряжения и скорости деформации связаны законом Стокса,
3)вязкость жидкости постоянна.
Двумерные уравнения Навье-Стокса для несжимаемой жидкости с постоянной вязкостью, при отсутствии массовых сил, можно получить из трехмерной системы (2.12), положив w = 0, gi = 0.
|
|
+ |
|
+ |
|
= − |
1 |
|
|
+ η∆ , |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
+ |
|
+ |
|
+= − |
1 |
|
|
+ η∆ , |
(2.13) |
||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
+ = 0
Эта система замкнута: 3 уравнения для 3-х неизвестных u, v, p . Чтобы математическая модель течения была полностью определена, следует задать краевые условия. Начальное условие
t 0 : u 0, v 0 , |
(2.14) |
означает, что движение начинается из состояния покоя.
Граничные условия для скорости могут выглядеть так.
На стенках канала y H ставится условие прилипания, согласно которому нормальная и касательная скорости на стенках равны нулю:
y H : u 0, v 0 , |
|
(2.15) |
||||
При этом равенство u 0 означает отсутствие скольжения, а условие |
v 0 |
|||||
отражает тот факт, что стенка канала непроницаема для жидкости. |
|
|
||||
На входе в канал задается профиль скорости, т.е. эпюра. |
|
|
||||
x -L1 : u u0(y); v 0 , |
|
(2.16) |
||||
На выходе из канала ставятся т.н. «мягкие» условия |
|
|
||||
x -L2 : |
|
0 ; v 0 , |
|
(2.17) |
||
|
|
|||||
которое означает, что в выходном сечении за телом течение близко к плоско- |
||||||
параллельному (v 0) , и его характеристики не меняются |
|
0. |
|
|
||
|
|
|
||||
|
|
|
|
|
|
|
На поверхности тела обычно тоже задают условия прилипания |
|
|
||||
(x , y) : vn = u cos(n , x) + v cos(n ,y) = 0, v |
0. |
(2.18) |
||||
Кроме условий для скорости на всех границах, требуется и одно условие для давления. Можно, например, задать постоянное давление на входе в канал
|
23 |
x -L1 : P p0 |
(2.19) |
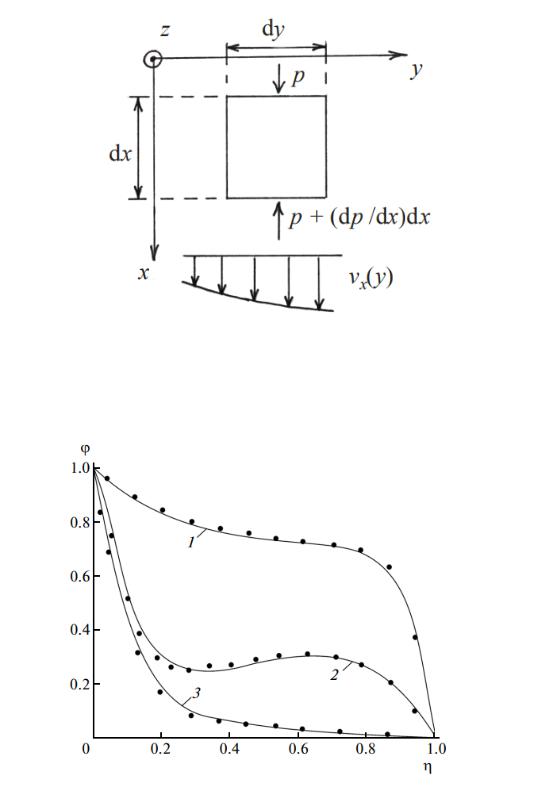
Рис. 2.2. Равнодействующая сил давления на верхнюю и нижнюю грани
Результаты задачи в графическом виде могут также быть представлены в виде как на рисунке 2.3, 2.4.
Рис. 2.3. Распределения температуры в плоскостях симметрии, расположенных под углами 0 градусов (линия 1), 90 градусов (линия 2) и 180 (линия 3) градусов к вертикальной
плоскости
24
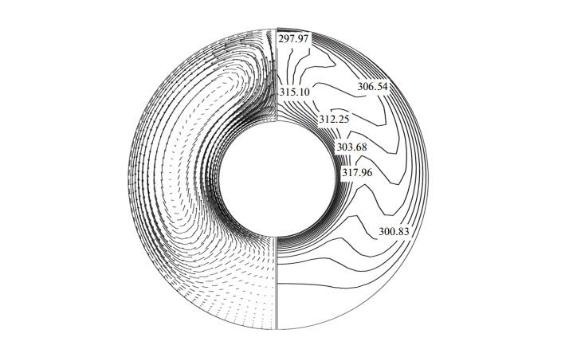
Рис. 2.4. Векторное поле скорости (слева) и линии уровня температуры (справа).

25
2.3.7 Раздел 2: 2.2 ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
Одной из разновидностей моделирования является численное моделирование, которое заключается в получении данных о поведении модели каким-либо подходящим численным методом, таким как методы Эйлера и Рунге Кутта.
На практике моделирование нелинейных систем и устройств с использованием численных методов оказывается намного более эффективным, чем аналитическое моделирование отдельных частей линейных цепей, систем или устройств.
Использование численных методов в настоящее время является достаточно эффективным ввиду хорошо разработанного специального программного обеспечения и наличия вычислительных систем высокой производительности. Все это способствует тому, что класс уравнений, которые могут быть решены численно значительно шире, чем класс уравнений, доступных аналитическому решению. Однако численные решения являются менее полными по сравнению с результатами аналитического моделирования. Использование численного моделирования, хотя и не требует получения аналитических выражений, связывающих искомые величины с входными параметрами исследуемой системы, предполагает представление математической модели в виде некоторой системы уравнений, устанавливающих соотношение между входными параметрами и искомыми величинами. При построении моделей сложных или недостаточно изученных систем, часто построение такой системы уравнений оказывается невозможным. В таких случаях прибегают к использованию имитационного моделирования.
Пример 1. Численное моделирование процессов тепломассопереноса для конвективных пучков котла.
Проведено численное моделирование процессов тепло и массопереноса в каналах кожухотрубного теплообменника с компактным размещением пучков труб, используя программный пакет ANSYS Fluent. Получены поля скоростей, и температур в исследуемых пучках труб. Проанализировано влияние геометрии на условия теплообмена и гидравлические потери в компактных поперечно обтекаемых пучках труб.
Пучки гладких цилиндрических труб с шахматным и коридорным расположением широко используются в различных теплообменных аппаратах (ТА) и устройствах энергетических установок. Обзор литературных источников и результатов значительного количества экспериментальных исследований тепло гидродинамических характеристик пучков гладких труб при поперечном обтекании, в том числе исследований по теплоотдачи шахматных пучков при высоких числах Рейнольдса показывает, что такие пучки имеют высокую теплоотдачу по сравнению с коридорными пучками. Однако при этом они имеют более высокое гидравлическое сопротивление по сравнению с коридорными пучками.
Проведено математическое моделирование гидродинамических процессов и процессов переноса теплоты в каналах с разным размещением пучков труб. Для этого использован метод компьютерного (CFD) моделирования с использованием программного комплекса ANSYS Fluent 14.0. В основе математической модели лежат уравнения Навье-Стокса и уравнения переноса энергии для конвективных течений. В расчетах применено стандартную k-ε модель турбулентности. Расчеты проведены для 3 конструкций со смещением конвективных труб.
Метод исследования
Моделирование турбулентного течения проводилось с помощью трехмерных уравнений Навье—Стокса, осредненных по Рейнольдсу (ReynoldsAreragedNavier—Stokes, или
RANS):
Уравнение сохранения массы:
(2.32)
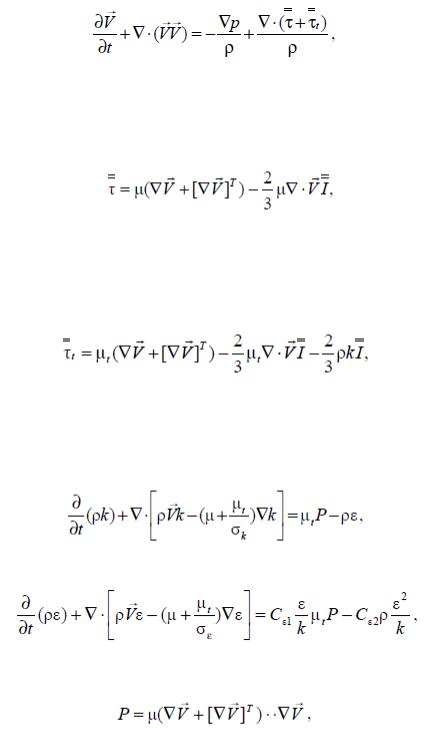
26
Уравнение сохранение импульса
(2.33)
где тензор вязких напряжений , определен с помощью реологического закона Ньютона:
(2.34)
а тензор турбулентных напряжений t для линейных моделей – в соответствии с обобщенной гипотезой Буссинеска:
(2.35)
Для нахождения характеристик |
турбулентности |
использована k-ε модель |
турбулентности: |
|
|
|
|
(2.36) |
(2.37)
генерационный член в уравнениях переноса (2.15) и (2.16):
(2.38)
где k — кинетическая энергия турбулентности; ε — скорость диссипации− кинетической энергии турбулентности; μt – турбулентная вязкость; Сε1, Сε2 — полуэмпирические коэффициенты модели турбулентности.
Данный подход моделирования турбулентности является в настоящее время наиболее широко используемым при решении практических задач и позволяет получить трехмерные поля скорости и давления по объему воздуховода, трения и давления на твердые поверхности частиц. Анализ полей показывает сложную структуру взаимодействия потоков в трубе при обтекании систем шарообразных частиц.
27
В расчетах использовалась k-ε модель турбулентности. Дискретизация исходных уравнений осуществлялась методом контрольного объема. Поля скорости и давления рассчитывались с помощью процедуры PISO в сочетании с многосеточным алгоритмом AMG.
В процессе математического моделирования изучены особенности формирующегося вблизи частиц скоростного поля и распределение давления по поверхности частиц. Для определения суммарной силы давления на частицы вычислялся интеграл давления по их поверхности.
Построение конечно элементной модели уходит больше времени, чем на выполнение любой другой части анализа. В Space Claim построила 3D модель котла КВа-3,5-95ГМ. Для дальнейшего сравнения задач построила сразу 2 модели с коридорным и шахматным расположением пучков. В дальнейшем задача будет решаться в 2D. Будем рассматривать 3 модели расположения пучков: с коридорным, шахматным расположением и с добавлением стержней в
коридорный тип.
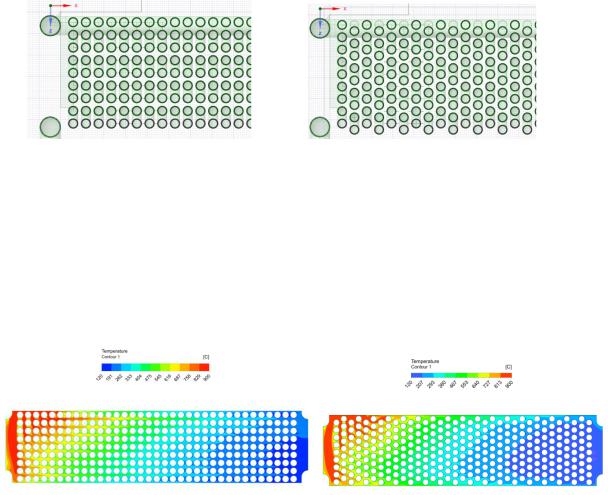
Рис. 2.5. Сечение участков конвективных пучков (слева участок коридорный, справа шахматный) Чтобы убедиться в эффективности изменения геометрии вводим одинаковые исходные
данные для всех случаев:
-Температура на входе – 900 ˚С
-Скорость потока – 4,52 м/с
-Температура воды в трубочках – 90 ˚С
После того, как решение сошлось, делаем первые сравнительные выводы для коридорного и шахматного расположения пучков:
Рис. 2.6. Распределение температур в коридорном и шахматном расположении пучков Шахматное расположение конвективных пучков оказалось эффективнее в распределение
потоков скорости и в процессе теплопередачи.
Потому что в коридорном типе потоки скорости распределяются не равномерно, а теплопередача получилась менее интенсивной.
При использовании шахматного расположения трубочек, зона низких температур (темносиняя по шкале) началась раньше на 7 рядов, что говорит о повышении комплексной интенсивности теплоотдачи ориентировочно на 20 %.
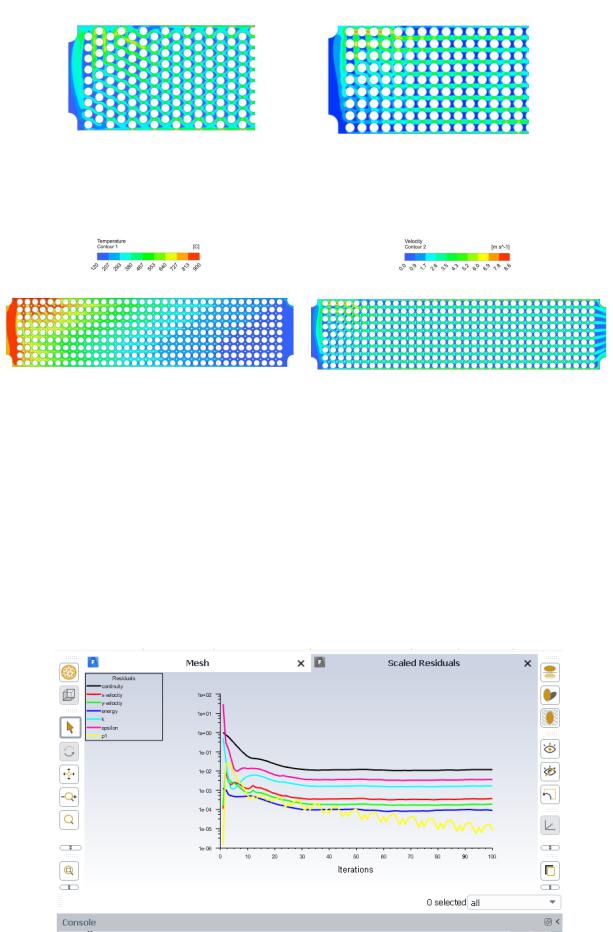
28
Рис. 2.7. Сравнение распределения скоростей в шахматном и коридорном расположение пучков. Для оптимизации пучков коридорного типа добавим стержни диаметром 20 мм между
трубочками. Соответственно применив те же настройки и данные для будущего сравнения.
Рис. 2.8. Изменение температуры и распределение потоков скорости в коридорном типе с добавлением стержней
Добавив стержни в коридорный тип расположения конвективных пучков, улучшили распределение потоков скорости и также оптимизировали теплопередачу. Зона низких температур (темно-синяя по шкале) началась раньше на 3 ряда, что говорит о повышении
комплексной интенсивности теплоотдачи ориентировочно на 8,5 %.
Сравнив 3 модели расположения конвективных пучков, можно сделать вывод о том, что шахматное расположение самое выгодное. В настоящее время именно изменением геометрии добиваются оптимизации теплопередачи в пучках конвекции колтов.
Компьютерное моделирование дает возможность проанализировать условия гидродинамического течения и теплопереноса в исследуемых каналах и определить их эффективность.
29
Рис. 2.9. График решения задачи.
2.3.8 Раздел 2: 2.3 КОНЕЧНО-РАЗНОСТНАЯ СХЕМА ЗАПИСИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.
Метод конечных разностей (или метод сеток) является одним изуниверсальных и широко используемых методов решения краевых задач. Его популярность во многом объясняется относительной простотой подхода кдискретизации дифференциальных уравнений. В качестве примера использованияконечно-разностного метода решения можно использовать систему уравнений Новье-Стокса.
Определяющие уравнения для турбулентных течений характеризуются в общем случае сильной нелинейностью, а численные свойства нелинейных дифференциальных уравнений ещё недостаточно изучены. Для турбулентных течений справедливы те же уравнения сплошности, движения и энергии, которые описывают ламинарные течения. Единственное различие между соответствующими двумя системами уравнений заключается лишь в том, что при турбулентных течениях зависимые переменные (например, Vx, Vy, p и t) интерпретируются как мгновенные величины (при осреднении по времени), каждая из которых в соответствии с аппроксимирующим выражением представляется суммой осреднённого значения и пульсации, причём предполагается, что осреднения как по времени, так и по ансамблю эквивалентны (эргодическая гипотеза).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.39) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|||||||||
( |
|
+ |
|
|
|
) = ( − |
) − |
|
|
+ ( |
|
|
|
+ |
|
) |
(2.40) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
2 |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
||||||||||||
|
( |
|
|
+ |
|
|
|
) = − |
|
|
+ ( |
|
|
|
+ |
|
|
) |
|
|
(2.41) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
( |
|
+ |
|
|
) |
= ( |
2 |
+ |
|
2 |
|
|
) |
|
|
|
|
(2.42) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
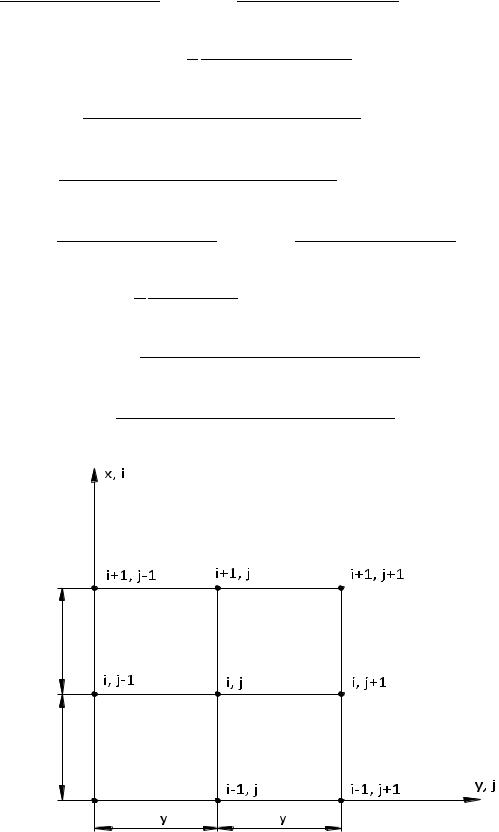
Система уравнений (2.39) - (2.42) решалась численно методом конечных разностей. Для этой цели область течения, занимаемая жидкостью, разбивалась разностной сеткой с шагом (i,j), где i,j – индексы узлов сетки. Для примера разностная сетка для четырёх точек в начале координатных осей показана на рис. 4.8.
При шаге по координатным осям 0,0001 м. получена система уравнений, которая в результате элементарных преобразований приведена к треугольной матрице, т. е. была решена. Система уравнений в матричном виде приведена ниже.
Уравнения (2.39)- (2.42) для точек в конечно-разностном виде записываются следующим образом.
Точка (i,j):
( , ) − ( − 1, ) |
|
( , ) − ( − 1, ) |
|
|
||||
|
|
|
+ |
|
|
|
= 0 |
(2.43) |
|
|
|
|
|||||
|
|
|
|
|
||||
30
( , ) − ( − 1, ) |
|
( , ) − |
( − 1, ) |
|
||||||
( , ) |
|
|
|
|
|
+ ( , ) |
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||||
|
= ( |
− |
|
) − 1 ( , ) − ( − 1, ) |
|
|||||
|
|
|
, |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
+ |
|
( − 1, ) |
− 2 ( , ) |
+ ( + 1, ) |
(2.44) |
||||
|
( |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
( , − 1) − 2 ( , ) + ( , + 1) |
|
||||||
|
+ |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
( , ) − |
( − 1, ) |
( , ) − ( − 1, ) |
|
|||||
( , ) |
|
|
|
|
+ |
( , ) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
− |
|
|
|
|
|
|
|
= − |
|
, |
, −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
( − 1, ) − 2 ( , ) + ( + 1, ) |
|
||||
|
|
|
+ ( |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
( , − 1) − 2 ( , ) + ( , + 1) |
|
|||||
|
|
|
+ |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Рис. 2.10 Разбивка области разностной сеткой |
|
||||||||
31
|
|
− |
|
|
|
|
− |
|
|
|
|
|||
( , ) |
, |
−1, |
+ |
( , ) |
, |
, −1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
(2.45) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
− 2 |
|
+ |
|
− 2 |
+ |
|||||
|
|
= ( |
|
−1, |
, |
|
+1, |
+ |
, −1 |
, |
, +1 |
) |
||
|
|
|
|
2 |
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Примерный перечень вопросов (к зачёту с оценкой):
1.Теплота. Плотность теплового потока. Законы Фурье, Фика, Ома, Ньютона.
2.Перенос тепловой энергии и массы.
3.Естественная конвекция.
4.Вынужденная конвекция.
5.Градиент потенциалов. Градиент температуры. Градиент концентраций.
6.Краевые условия – условия однозначности.
7.Общая постановка задачи моделирования процессов теплопередачи.
8.Общая постановка задачи моделирования процессов теплопроводности,.
9.Общая постановка задачи моделирования процессов теплообмена,.
10.Общая постановка задачи моделирования процессов тепломассообмена.
11.Постановка задачи теплопередачи при определённых граничных условиях.
12.Термодинамика состояния рабочих веществ.
13.Приближённый метод расчёта тепловлажностного состояния воздуха и газов.
14.Общие понятия об основных видах физико-математического описания процессов тепломассопереноса в аппаратах.
15.Описание процессов на основе уравнения Рейнольдса.
16.Описание процессов на основе уравнения пограничного слоя.
17.Описание процессов на основе одномерного переноса (α-модель).
18.Особенности тепломассопереноса в оребрённых теплообменниках.
19.Модели тепломассообмена в аппаратах систем ТГВ.
20.Основные числа подобия, характеризующие теплопроводность.
21.Основные числа подобия, характеризующие конвективный теплообмен жидких и газообразных сред.
22.Основные числа подобия, характеризующие конвективный массообмен жидких и газообразных сред.
23.Основные числа подобия, характеризующие конвективный тепломассообмен жидких и газообразных сред.
24.Основные числа подобия, характеризующие лучистый теплообмен.
25.Основные числа подобия, характеризующие теплопередачу.
26.Эксперименты и их анализ.
27.Теоретические основы течения жидкостей в каналах.
28.Теоретические основы течения газов и воздуха в каналах.
29.Особенности тепломассообмена при течении жидкостей, газов и воздуха в каналах.
30.Моделирование установившегося движения жидкости в напорных трубопроводах.
31.Моделирование неустановившегося движения жидкости в напорных трубопроводах.
32.Моделирование установившегося движения газа или воздуха в напорных трубопроводах.
33.Моделирование неустановившегося движения газа или воздуха в напорных трубопроводах.
34.Моделирование установившегося движения жидкости в открытых системах.
35.Моделирование неустановившегося движения жидкости в открытых системах.
36.Моделирование установившегося движения газа или воздуха в открытых системах.
